基于ABAQUS和有限元法的金属丝拉伸过程数值模拟
吴世宝,马 佳,马瀚龙,高 婧
(1. 沈阳航空航天大学航空宇航学院,110136,沈阳;2. 沈阳航空航天大学理学院,110136,沈阳;3. 沈阳航空航天大学创新创业学院,110136,沈阳;4. 沈阳航空航天大学能源与环境学院,110136,沈阳)
0 引言
金属材料以其强度高、硬度大、抗冲击能力强等优越的力学特性,被广泛地应用于机械零件、工程构件以及其他工业领域中。由金属材料制作成的零件或构件在承受外载荷时,金属材料的力学性能(例如弹性模量、伸长率等)对零件或构件的工作状态有很大的影响[1]。因而,研究金属材料在承受外载荷时的力学性能对改善由金属材料制成的零件或构件的工作性能具有十分重要的意义。
拉伸是工程领域中零件或构件经常承受的一种外载荷[2]。对于金属材料在拉伸时力学性能的测试方法,国家标准规定,应使用微机控制的万能试验机拉伸标准实验试样,且试样的形状多为圆柱体棒料[3]。而对于工程中同样较为常用的细长的金属丝一类的材料,实验室环境下一般采用YMC-I型或YMC-II型杨氏模量测量仪[4],在利用光杠杆测定金属丝的伸长量以及弹性模量的同时,对金属丝在拉伸时的力学性能进行研究。在使用杨氏模量测量仪进行实验时,需要用钩码对金属丝进行加载并使用光杠杆,结合微小放大法的原理,测量金属丝的伸长量[5-7]。这样的实验步骤在实际操作过程中十分繁琐,由此带来的误差有可能导致无法获得正确的实验结论。随着计算机技术和有限元理论[8-9]的不断发展,应用CAE软件对此类实验过程进行仿真模拟越来越受到人们的青睐,这些CAE软件的出现正逐步将人们从复杂的实验过程中解放出来,让人们更加注重对材料力学性能的研究。
基于上述分析,本文首先利用YMC-1型杨氏模量测量仪,并结合本文开发的一款Python GUI数据处理系统,测定了某条金属丝在外力作用下的伸长量并利用逐差法计算出它的弹性模量。随后,利用上述实验中测得的数据,在ABAQUS软件中对这条金属丝的拉伸(加载)过程进行数值模拟。最后,将ABAQUS软件利用有限元法计算出的该金属丝的伸长量与实验中测得的该金属丝的伸长量进行对比,以判断ABAQUS软件的数值模拟结果是否合理。
1 金属丝拉伸实验
1.1 实验原理
设有一条长为L,且横截面积为A的金属丝,沿其长度方向施加大小为F的外力,金属丝的伸长量为△L。由胡克定律,得该金属丝的弹性模量E的表达式为
(1)
实验中,由多个质量均为1 kg钩码来提供大小不同的外力F。此外,可以用千分尺测得金属丝的直径D,进而计算出金属丝的横截面积A。金属丝的长度L可以通过米尺测得。金属丝的伸长量△L可以利用光杠杆法进行测量,其原理如图1所示[10]。

图1 光杠杆原理图
由图1中的几何关系可知
(2)
其中:B是读数的望远镜到光杠杆的距离,b是光杠杆常数,且B和b均可由米尺测出。△n为标尺上某次加载时的读数ni与初始读数n0之差。将式(2)代入式(1),可得金属丝的弹性模量E的表达式为
(3)
1.2 实验数据
实验中主要需要测量金属丝的直径D和不同外力F作用下标尺的读数ni,这里主要对这两类物理量的测量进行介绍。首先介绍用千分尺测量金属丝的直径D的过程。由于千分尺经过长期使用,往往存在着初始读数非0的系统误差,因而在测量前需要记录千分尺的初始读数,在本实验中所使用的千分尺的初始读数D0=-0.015 mm。修正初始读数后,测量了金属丝5个不同位置的直径,如表1所示。在代入式(3)计算时,需要将表1所示的5个直径取平均值,作为金属丝的平均直径D。

表1 金属丝直径的测量值


表2 标尺读数
1.3 数据处理
参考表1和表2的数据内容,本文设计了一种用逐差法处理本实验数据的Python GUI界面[11-12],如图2所示。此界面主要分为3个工作区域,如图2中3个线框所示。
由图2可知,在使用时,用户只需要将测得的实验数据和相关的不确定度数值根据提示输入区域A,然后点击下方区域B中的按钮,即可在区域C中查看相应的计算结果。点击“保存报告”按钮,可以将完整的实验报告保存到工作路径下。另外,区域B下方的“历史命令”窗口能显示用户对区域A中的实验数据进行了哪些操作。
将表1和表2中的数据以及其他参数按提示输入区域A,随后依次点击区域B中的“直径”、“伸长量”和“弹性模量”3个按钮,可以在区域C中分别查看对应的结果;若直接点击“完整报告”按钮,则区域C将一起显示上述所有物理量的计算结果,如图3所示。

图3 完整计算结果
由图3可知,金属丝的平均直径D=0.587 mm,弹性模量E=211 GPa,这2个数据将用在接下来的数值模拟中。此外,本文也从图3中获得了不同外力作用下金属丝的伸长量及其不确定度数值,如表3所示。
由表3可知,随着金属丝所受外力F的增大,金属丝的伸长量△L也随之增大。此外,随着金属丝的伸长量△L的增大,其对应的不确定度数值也在增大,可见当金属丝所受外力F较大时,金属丝伸长量的不确定度也较大,这意味着这种测量金属丝伸长量的方法在金属丝承受较大载荷时可能存在局限性。
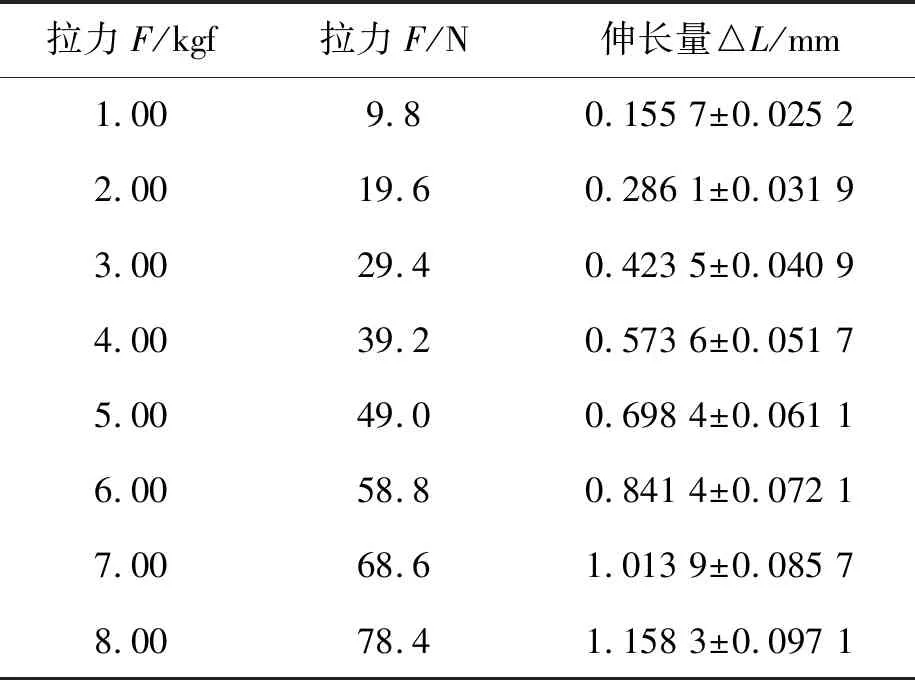
表3 金属丝的伸长量
2 加载过程的ABAQUS数值模拟
2.1 金属丝的有限元模型
在ABAQUS软件中,建立金属丝的有限元模型[13]主要需要经历以下几个步骤:1)在“部件”模块中建立金属丝的几何模型;2)在“材料”模块为金属丝赋予对应的材料属性;3)在“网格”模块为金属丝的几何模型划分网格。上述建立有限元模型的过程如图4(a)~(d)所示。
由图4(a)和(b)可知,在建立金属丝的几何模型时,金属丝的截面半径为0.29 mm,金属丝的长度为828.5 mm;由图4(c)可知,由于金属材料在未发生屈服前均满足胡克定律,且沿各个方向的力学性能相同,因而金属丝的力学行为是“弹性”类型中的“各向同性”。对于各向同性材料需要定义其弹性模量,此金属丝的弹性模量已经由拉伸实验测出,大小为211 000 MPa;由图4(d)可知,在为金属丝的几何模型划分网格时,选取的扫掠算法是中性轴算法,此算法共划分了43 128个网格单元。经历如图4(a)~(d)所示的各个步骤,完成了金属丝有限元模型的建立,最终建立好的金属丝的有限元模型如图5所示。

(a)定义金属丝的截面尺寸 (b)定义金属丝的长度

(c)定义金属丝的材料属性 (d)定义网络属性
图5中的圆柱体就是金属丝的几何模型,几何模型上也出现了划分好的网格。与此同时,金属丝有限元模型的颜色变成了蓝色,说明材料属性已经赋予给了此有限元模型。由于金属丝的长度较长,图5中仅展示了加挂钩码一端的有限元模型,该金属丝其余部分的有限元模型与图5中所示的有限元模型是相同的。

图5 金属丝的有限元模型
2.2 分析步、边界条件与载荷
在实验中,金属丝所受的外力F是从1个钩码依次增加到8个钩码,所以金属丝的加载过程并不连续,因而需要通过设置多个分析步的方式来模拟从1个钩码依次加载到8个钩码的加载过程,如图6所示。

图6 设置分析步
由图6可知,加载的过程一共设置了9个分析步,其中包括1个初始分析步(Initial)和8个静力、通用分析步(Step-1~8),其中初始分析步Initial用于设置初始的边界条件,静力、通用分析步用于施加载荷。
接下来需要在初始分析步Initial中设置符合实验情况的边界条件,设置边界条件的对话框如图7所示。
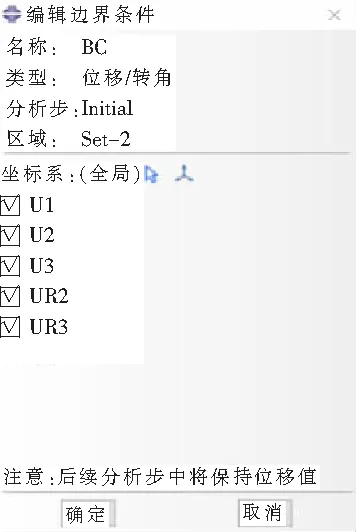
图7 设置边界条件
在实验中,金属丝一端受到钩码的拉力,另一端被夹持在杨氏模量实验仪中,在x、y、z3个方向上没有位移和转角。因而,可以选择图7中所示的“位移/转角”这一类型的边界条件中对3个方向上的位移(U1、U2和U3)以及转角(UR1、UR2和UR3)进行约束。
最后需要在剩余8个静力、通用分析步中施加载荷。由于ABAQUS软件是利用压强来定义载荷大小的,所以在定义金属丝加载时所受的载荷前,首先需要用金属丝所受的外力F除以金属丝的横截面积A,以得到不同的外力对应的压强。取金属丝的直径为0.587 mm,则不同的外力对应的压强如表4所示。
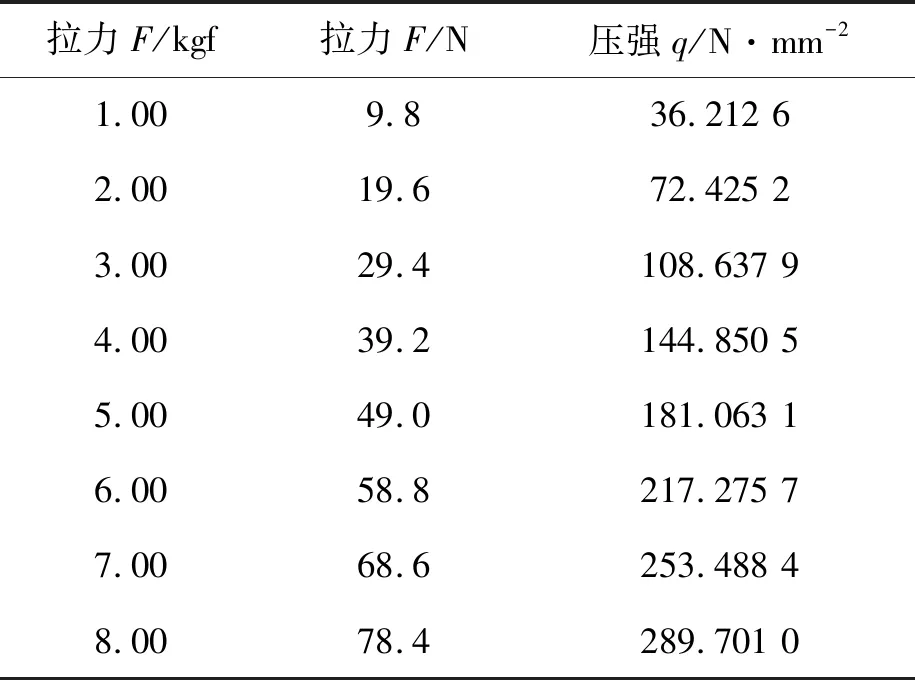
表4 不同外力对应的压强
接下来需要将表4所示的载荷设置到Step-1~8这8个静力、通用分析步中。显然,Step-1~8和从1个钩码增加到8个钩码的加载过程是一一对应的,如图8(a)~(c)所示。
由图8(a)可知,当加挂1个钩码时,可以在Step-1中设置大小为36.212 6 MPa的压强,其中负号表示向外拉伸,不表示大小。由于后续的分析步可以继承前面已经设置的分析步中的载荷,所以在定义分析步Step-2~8中的载荷时,载荷的大小为此分析步与前一个分析步所设置的载荷大小的差值。例如,在Step-2中定义载荷时,其压强的大小为2个钩码对应的压强与1个钩码对应的压强之差,即36.212 6 MPa,如图8(b)所示。按照类似的方法,可以定义Step-3~8中的载荷大小,所有定义完成的载荷如图8(c)所示。由图8(c)可知,从分析步Step-2开始,每一个分析步都传递了之前分析步中设置的载荷。每个分析步之间载荷的传递,使得分析步Step-1~8中每个分析步里的总载荷与表4所示的8个外力对应的压强分别相等,以模拟不连续加载的过程。

(a)Step-1中的载荷 (b)Step-2中的载荷 (c)Step-1~8中的载荷
2.3 数值模拟结果
将金属丝的有限元模型以及定义的分析步、边界条件和载荷提交,ABAQUS软件将根据有限元法计算出金属丝各处的位移。在实验中,利用光杠杆测出的伸长量为金属丝加挂钩码一端的伸长量。在ABAQUS软件中,由于施加的是轴向载荷,其轴向位移的大小与全位移的大小相等,因此,本文以施加拉伸载荷的截面上各个节点的位移的平均值作为ABAQUS软件计算出的金属丝的伸长量。ABAQUS软件计算出的不同外力作用下金属丝加挂钩码一端的位移云图如图9(a)~(h)所示。

图9 金属丝的位移云图
由图9(a)~(h)左上角的图例可知,随着颜色的加深,金属丝的位移也在增大,且金属丝加挂钩码一端都显示为最深的颜色,说明金属丝在该处的位移为最大;除此之外,图9(a)~(h)中的△L值就是施加拉伸载荷的截面上各个节点位移的平均值,如表5所示。
由图9和表5可知,金属丝的伸长量与图例中显示的金属丝的最大位移相差不大,且随着载荷的增大,金属丝的最大位移也在成比例地增大,从数据的变化趋势来看基本上符合了胡克定律的特征。由此可以做出一个初步的判断,即ABAQUS的数值模拟结果与实际情况基本吻合。
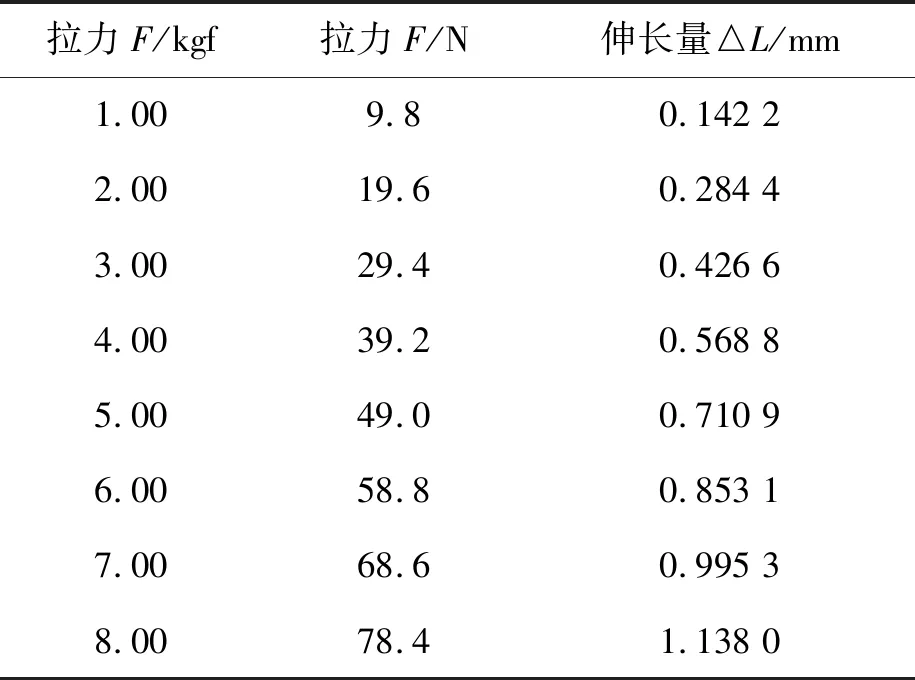
表5 ABAQUS数值模拟结果
3 实验结果与数值模拟结果的对比
3.1 结果对比
将表3所示的通过拉伸实验测得的金属丝的伸长量及其不确定度与表5所示的ABAQUS软件的数值模拟的结果绘制在同一个△L随F变化图像中,如图10所示。
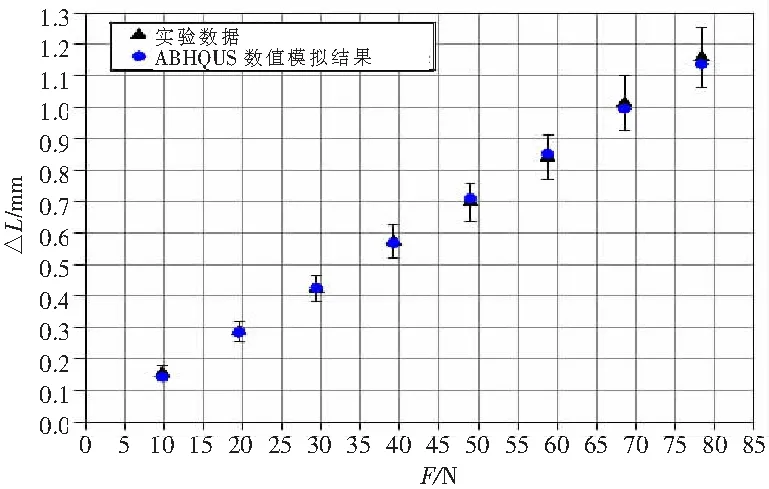
图10 实验数据与ABAQUS数值模拟结果的对比
由图10可知,实验数据的数据点和ABAQUS数值模拟结果的数据点基本重合,且△L的最大相对误差为8.67%。由此可见,ABAQUS软件对金属丝加载过程的数值模拟是较为准确合理的。
3.2 误差分析
除去仪器本身的系统误差以及人为读数所引起的误差,造成实验数据和仿真数据之间存在差异的主要原因应为物体本身的“力滞效应”,即物体受到外力作用后,并不会马上发生形变,也就是说物体形变的过程需要一定的时间,这也正是在拉伸实验时要先加载后卸载的原因,这样做的目的是减小“力滞效应”对实验的影响。然而,在ABAQUS软件利用有限元法进行计算时,没有将这一效应进行充分地考虑,因而造成了实验数据和数值模拟结果之间存在一定的差异。事实上,这种差异可以通过在ABAQUS软件中设置更为详细的材料属性来避免,这也是后续研究的主要工作方向。
4 结束语
本文利用了从拉伸实验中获得的金属丝的相关参数,结合有限元法,应用了ABAQUS软件对该金属丝的加载过程进行了数值模拟。通过将拉伸实验中测得的金属丝的伸长量与ABAQUS软件中计算出的金属丝的伸长量进行对比,本文认为,ABAQUS软件的数值模拟结果与实验所得到的数据能够很好地吻合,说明将有限元法应用在这种场合是合理的,为解决工程领域中其他类似的仿真分析问题提供了新思路。

