考虑换乘费用的城市公共交通票价优化

丛 丛，胡蔚旻

（1.广东交通职业技术学院 轨道交通学院，广东 广州 510650；2.华南理工大学 土木与交通学院，广东 广州 510641)

0 引言

公共交通泛指向大众开放、提供城市内部人员运输服务，按定线运营的多种交通方式的总称。公共交通相比于私家车，具有低碳环保、高运量、多方式、低成本和便利性等优点，因而在庞大出行需求压力下，即使私家车保有量飞速增长，公共交通仍然具有较大的吸引力和影响力，随着公共交通网络建设日趋复杂化。随之，换乘也逐渐成为居民出行的常态，其产生的时间、票价等附加费用将改变客流分配影响因素。如果以路径长度等作为参数的传统方式进行预测，将造成预测精度不足，线网预期效益偏差，降低预测可靠性。

早期公共交通线路配流多采用以路径长度为指标进行流量分配[1-2]，由于乘客选择出行路径时对最短路径的认知存在差异，导致配流结果与实际存在明显偏差。近年来，不少学者对路权的计算方法与配流原则进行改进[3-7]；姜虹等[8]提出乘客实际等待时间与因拥挤产生的延误时间的阻抗函数，将拥挤程度列为路权计算参数；李远等[9]通过建立随机用户均衡模型考虑增广公共交通网络中的入网、运行、换乘和出网时间，采用改进的相继平均法对路网进行配流；刘秉政等[10]将乘客主观评价和换乘优惠率列为乘客出行选择影响因素，建立双层规划模型求解最优票价及优惠率。方丽君[11]采用全局和局部更新相结合的方式改进蚁群算法中信息素更新原则，在保证精度的前提下提高模型运算速度。

因此，综合考虑乘客出行的换乘次数、方式、票价以及等待、乘车、换乘时间等因素，改进路权参数，建立以社会福利为上层模型、优化信息素更新原则的蚁群算法为下层出行需求配流模型，通过对双层规划模型的求解，实现公共交通的票价优化。

1 公共交通广义出行费用模型

1.1 广义费用模型

在城市公共交通网络中，乘客在选择公共交通出行时会出于票价、步行时间、路线长度、乘车时间、舒适度等多方面考虑。较于传统狭义出行费用，广义费用增加对换乘费用的考虑，换乘费用指在考虑换乘时间和方式因素下乘客出行时在换乘站点间的步行和等待换乘车辆的时间费用。基于李远等[9-10]的研究，对广义出行费用及相关参数进行如下定义。

时间费用包括等待、乘车、换乘及风险评估预留时间，假设各路段上的路段阻抗函数是相互可加的，则乘客出行起讫点OD路径中公共交通出行路径ij间第m条路径的出行行为中产生的所有时间和票价费用为广义出行费用U1m，计算公式为

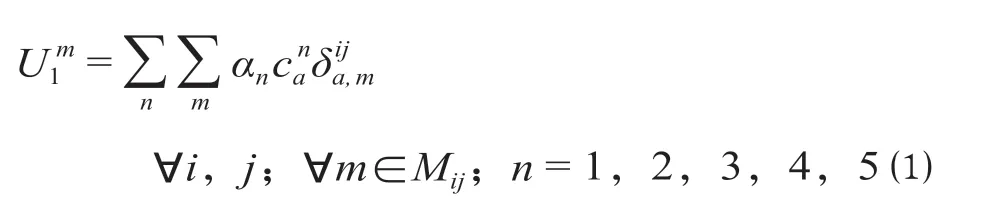
式中：α1，α2，α3，α4，α5为指标同一量化系数，如果乘车时间作为量化标准，则乘车时间量化系数α2= 1.0，相对应，α1，α3，α4为乘客的等待、换乘、风险评估预留时间价值与乘车时间价值的比值，α5为乘客乘车时间价值的倒数；a表示车辆运行路段；为等待时间，为乘车时间，为换乘时间，为风险评估预留时间，为票价；= 1 表示路段a∈M，否则= 0；M表示所有乘客出行路径的集合。其中等待时间，乘车时间，换乘时间，风险评估预留时间和票价参数定义如下。

1.2 模型参数

1.2.1 时间参数

（1）等待时间。乘客出行到达线网起点时，通常需要一定的等待时间才能上车，这里选取平均等待时间，等待时间计算公为

式中：fb表示公共交通的发车频率；参数γb取决于公共交通的车间时距和乘客到达公共交通线网起点的时间分布，如果乘客到站时间服从均匀分布，且公共交通的车间时距为定值，则参数γb= 0.5；A1表示路网各公共交通行驶路段集合。

（2）乘车时间。乘车时间为乘客在车辆中的逗留时长，包括信号灯和站点停靠等车辆停止行驶时间。车辆的拥挤度一定程度上影响乘客对实际乘车时间的认知，扩大乘客感知与实际乘车时间的偏差值。车辆运行路段a上基于乘客数量的拥挤系数ρ定义如下

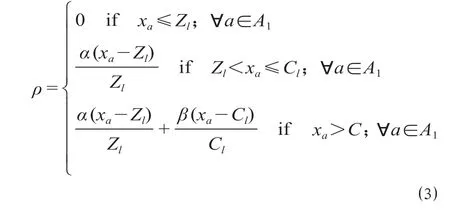
式中：xa表示车辆运行路段a上的乘客量；Zl，Cl分别表示公共交通线路l的一辆公共交通的座位数、容量；a，β是相应的参数。

此外，通过BPR 函数描述基于车辆拥挤的乘车时间。简化考虑，认为在车辆运行路段a上公共交通的运行时间ca2固定，即为运行路段长度la与在该路段上运行的属于公共交通线路 的运行公共交通的速度vl的比值，即

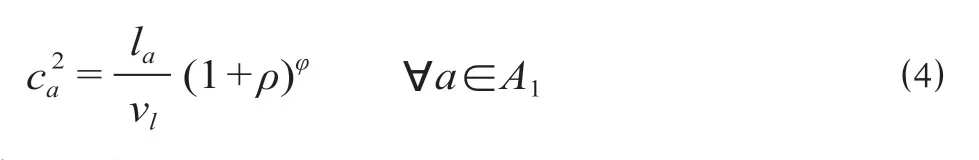
式中：φ是待标定参数，出于简便性考虑[12]，取φ= 1.0。

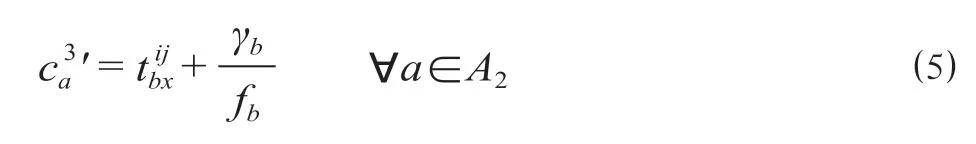
（3）换乘时间。换乘时间ca3包括换乘站点间的步行时间和等待换乘车辆时间，计算公式为式中表示乘客在换乘起讫点ij之间进行单次换乘的步行时间；A2表示路网各公共交通线路换乘网络集合。

出行过程中的换乘行为会在乘客心理上形成时间放大效应，且该效应与换乘次数、时间和方式相关，即更新定义换乘时间，更新后的换乘时间计算公式为

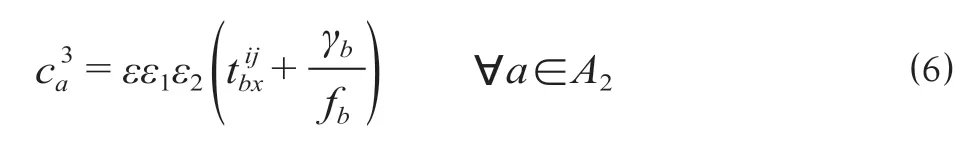
式中：ε(≥0)为乘客单次出行的换乘次数，ε1(≥1)为换乘时间惩罚因子；ε2( ＞1)为换乘方式惩罚因子[13]。

（4）风险评估预留时间。根据刘秉政等[10]研究发现，乘客依据对各路径公共交通乘车时间的可靠性风险评估，增设出行预留时间，从而增大出行总时间费用，对路网票价优化、乘客路径选择具有一定影响；研究基于乘车时间量化公共交通运行时间可靠性的风险，计算风险评估预留时间即

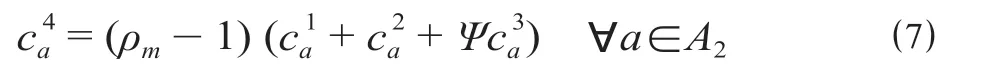
式中：ρm(＞1)是乘客对公共交通出行方式运行时间可靠性的风险度量参数；参数Ψ= 1 表示乘客进行换乘出行，反之Ψ= 0。

1.2.2 票价参数

目前采用的票价收费制度分为差异票价和单一票价；相比差异票价，单一票价的公平性、合理性有待提高，长、短距离出行乘客的票价支出未能与其造成的交通资源消耗量呈正相关。因此，采用阶梯式计费方案收取差异票价，以10 km 为基础票价乘坐路程，超过部分以5 km 为阶梯高度，逐阶增收基础票价的半价金额，票价ca5计算公式为

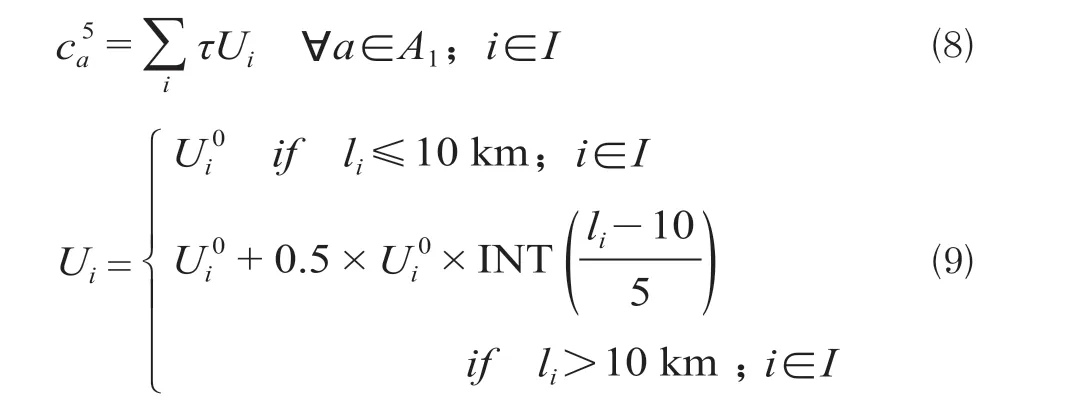
式中：参数τ= 1 表示乘客选择此公共交通线路出行，反之τ= 0；i表示所选公共交线路名称；Ui表示所选的i路公共交通线路的总票价；I表示路网中所有公交线路的集合；Ui0表示所选的i路公共交通线路的基础票价；li表示乘客乘坐i路公共交通线路的路程。

2 公共交通票价优化模型构建

票价的波动会对潜在客流量和路径配流造成影响，从而导致运营利润和乘客盈余的变动。因此，研究建立以改进信息素更新原则的蚁群配流算法为下层模型,社会福利为上层模型的双层模型。最后，利用改进蚁群算法求解下层模型进行路网配流，通过鱼群算法求解不同换乘费用下满足既定社会福利对应的最优票价，从而实现公共交通的票价优化。

2.1 下层模型构建

下层模型以蚁群算法为基础模型进行信息素更新原则优化，将包含时间、票价参数的广义出行费用替换传统蚁群算法中信息素更新原则的行驶总路径参数，使蚁群在路径选择时将出行时间和乘坐票价等因素纳入考虑。

乘客根据蚁群算法对出行路径进行选择，依据传统蚁群算法按轮赌法利用下式计算路径概率分布为

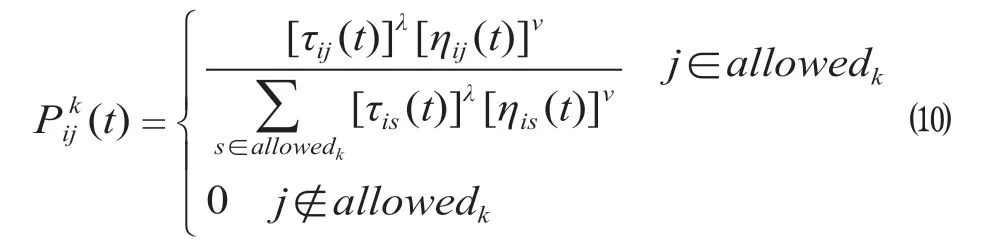
在优化问题上众多学者研究表明蚁周系统的算法性能优于蚁密系统、蚁量系统，计算方式为

式中：τij(t+ 1)，τij(t)表示当前循环中t+ 1，t时刻站点(i，j)间所有路径的信息素；ρ表示当前循环中信息素轨迹衰减后原信息素的保留系数，反映了信息素衰减作用的强弱；Δτij(t，t+ 1)表示所有蚂蚁在当前循环中路径(i，j)的信息素增加量，即本次循环结束时所有曾到达换乘站点i的蚂蚁在此换乘站点留下的选择换乘路线j的参考信息；q表示当前循环中蚂蚁的数量；表示蚂蚁k在当前循环中路径(i，j)的信息素增加量，即蚂蚁k在本次循环结束时在换乘站点i留下的选择换乘路线j的参考信息；Q表示蚂蚁循环一周时在途径路径上释放的信息素总量；Lk表示蚂蚁k在当前循环中经过的路径总长度。

基于传统蚁周系统算法思想，结合依据出行费用对公共交通票价进行优化，对蚁周系统进行改进为

式中：Uk表示蚂蚁k在当前循环中经过路径的出行费用。

采用上述改进蚁群算法进行求解时，通过设置迭代终止条件n=N避免陷入局部最优解；将人工蚂蚁q置于同一起点O上，并设置同一终点D进行迭代；每轮迭代后对各路径采用改进蚁周系统算法进行全局信息素更新，当满足终止条件时输出乘客流量分配表x(n)。

2.2 上层模型构建

基于下层配流模型对包含换乘费用、票价参数的弹性需求进行客流分配，依据配流结果计算以票价收入为指标的运营商利润，结合乘客盈余进行社会福利的上层模型计算，并以能够满足既定的社会福利值Saim为前提进行票价优化，其对应的票价上限值即为最优票价。

社会福利为乘客盈余与公共交通运营商利润之和[10]。根据Williams 以及Evans 的研究分析，当出行费用、乘客盈余以时间为衡量单位时，乘客盈余可以表示为式中：参数μ反应潜在出行需求量对期望出行广义费用的敏感程度为总的出行需求量。定义OD对第m条路径的出行需求量gm函数为

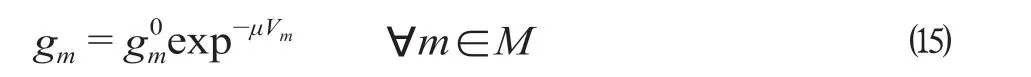
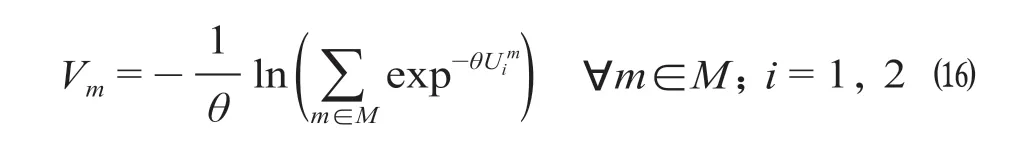
式中：θ(＞0)表示乘客对出行负效用的认知偏差。

此外，公共交通运营商利润π等于车票收入与运营总成本的差值，可以表示为

式中：xm表示第m条路径上的交通配流量；NC表示公共交通运营成本。

上层模型所求社会福利S可以量化为

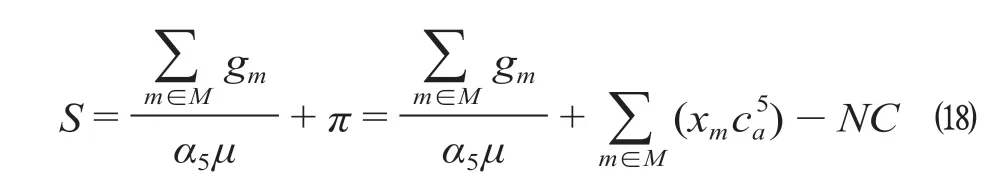
由于不考虑乘客出行费用的变化对公共交通运营成本的影响，为排除成本估算所造成的误差，社会福利目标函数仅考虑乘客盈余与票价收入的总和，表述为

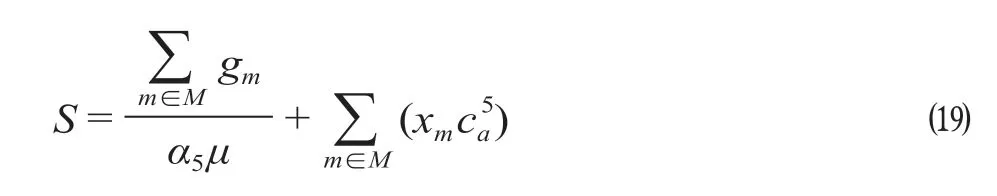
为避免模型优化过程陷入局部最优，选用具备良好并行处理能力的人工鱼群算法进行多变量的目标函数值最优化求解，防止模型因“早熟”而陷入局部最优，设置满足既定的社会福利值为终止条件S=Saim，计算并比较各代在不同换乘时间费用下达到终止条件的票价上限值，选取其中最大值即为最优票价U best。

3 公共交通票价优化算例分析

3.1 公共交通线路网络

结合李远等[9，18]所提出的公共交通网络，公共交通线路网络图如图1 所示，图1 中线段旁边的数字表示各公共交通线路，括号中的数字分别表示发车间隔(min)和平均速度(km/h)。采用图1 所示公共交通网络进行流量分配及票价优化，并从实际角度出发进行如下假设：①乘客不可以在同一站台多次换乘；②乘客出行路径中不可以间断出现在同一公共交通线路；③乘客一次出行的换乘次数不超过2 次。

3.2 计算结果分析

3.2.1 下层模型

首先对各路径流量分配进行比较，由于基于弹性需求对公共交通票价进行优化，换乘费用惩罚因子与票价的不同均会导致出行需求的差异与路径配流的变化，因此对路径流量分配进行标准化。广义出行费用中的换乘费用包含了换乘时间和方式惩罚因子参数，两者共同影响换乘费用，统称为换乘费用惩罚因子。通过计算可知为达既定社会福利，换乘费用惩罚因子取值范围为ε1ε2∈[1.1，2.1]，选取换乘费用惩罚因子ε1ε2= 1.1 和ε1ε2= 2.1 的2种情况为例进行对比分析。基于不同换乘费用惩罚因子路段流量分配图如图2 所示。各情形分配结果比较如表1 所示。各情形下换乘次数分布比如图3所示。各情形下各线路流量配比如图4 所示。

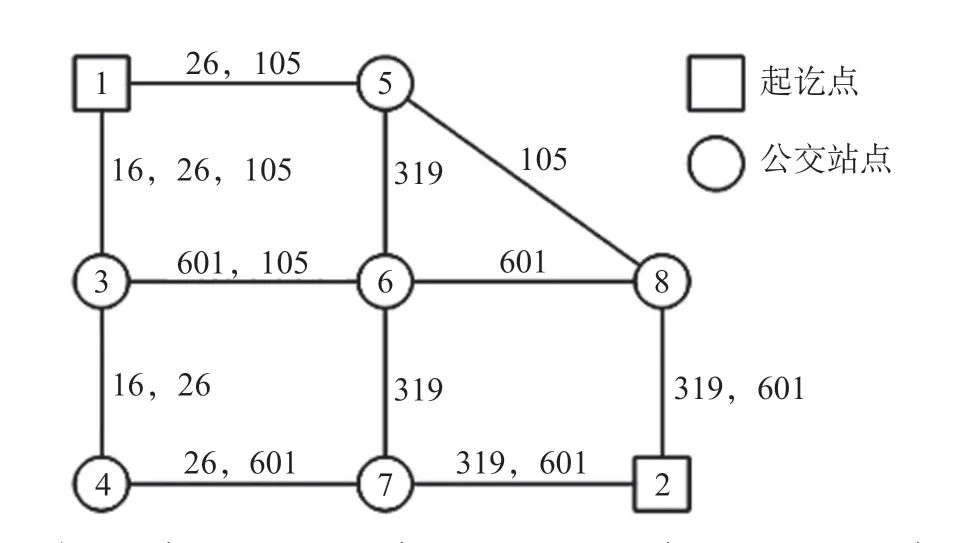
图1 公共交通线路网络图Fig.1 Line network map

比较发现，2 种情形中乘客选择1 次换乘的概率均高于2 次换乘，各情形中2 种换乘概率分布的差值分别为19.65%，28.09%；情形1 中乘客选择1 次换乘的概率低于情形2 的对应概率，两者概率差为-4.20%；而乘客选择2 次换乘的概率则高于情形2。情形2 由于强化了换乘费用因素，增加了换乘成本，因此乘客倾向于选择换乘次数少的路径，导致各路径间流量差值增大，即情形2 各路径流量分配值标准差大于情形1，提升11.90%。线路平均行驶时长大于约10.5 min 时，情形2 的概率分布低于情形1，累计下降概率1.32%，反之则情形2 概率更高，但由于时长为7.5 min，8.25 min时所对应的路径有较高的换乘次数，因此概率略有下降，分别降低0.15%，0.29%。

3.2.2 上层模型

由于选择公共交通出行的需求量和社会福利会随换乘费用、票价等出行费用的变化而波动，选取换乘费用惩罚因子与满足其条件下达到社会福利的最优票价 、出行需求 进行比较分析。换乘费用惩罚因子与出行需求的关系如图5 所示。票价与出行需求的关系如图6 所示。换乘费用惩罚因子与出行需求、票价的关系。

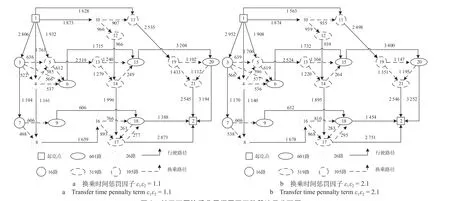
图2 基于不同换乘费用惩罚因子路段流量分配图Fig.2 Road traffic allocation map based on different transfer cost penalty factors

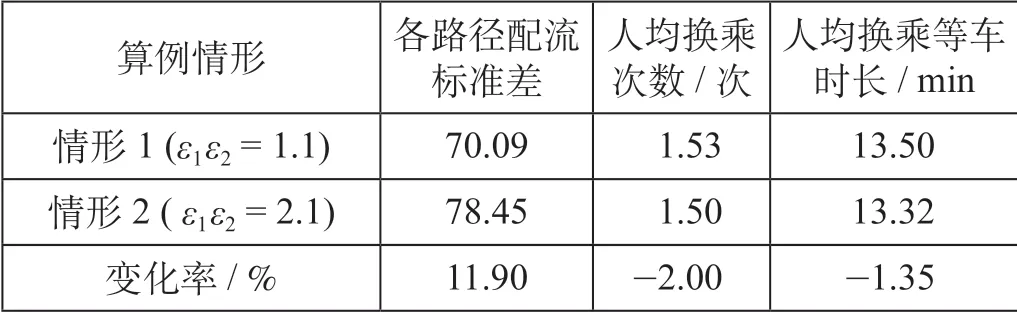
表1 各情形分配结果比较Tab.1 Comparison of the distribution results of each situation

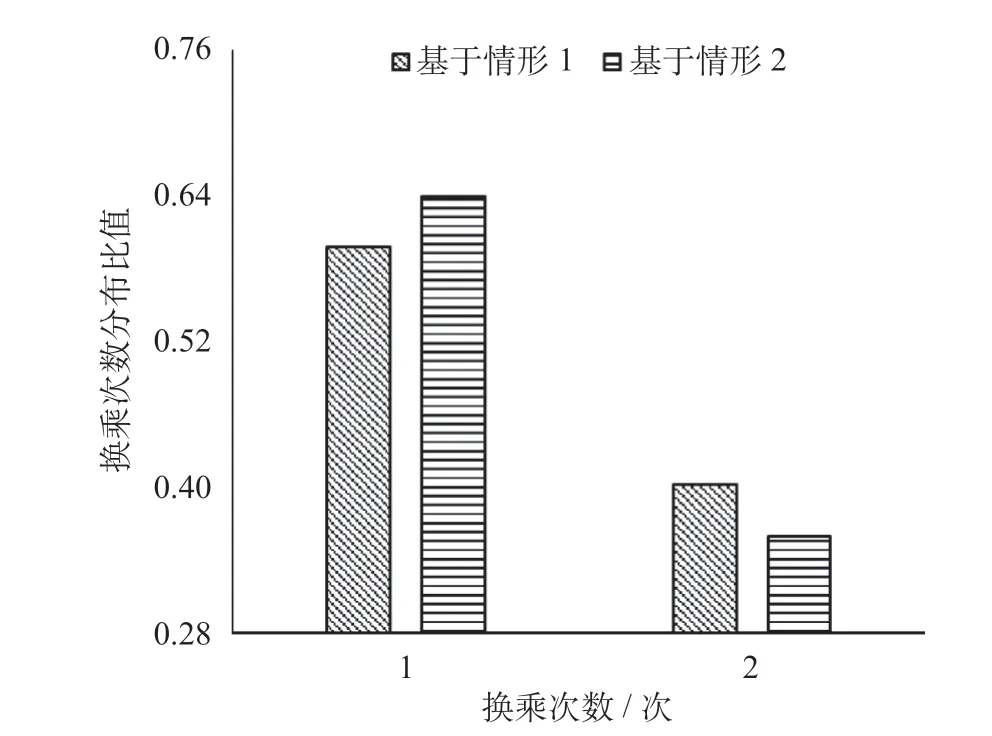
图3 各情形下换乘次数分布比Fig.3 Distribution ratio of transfer times in each case

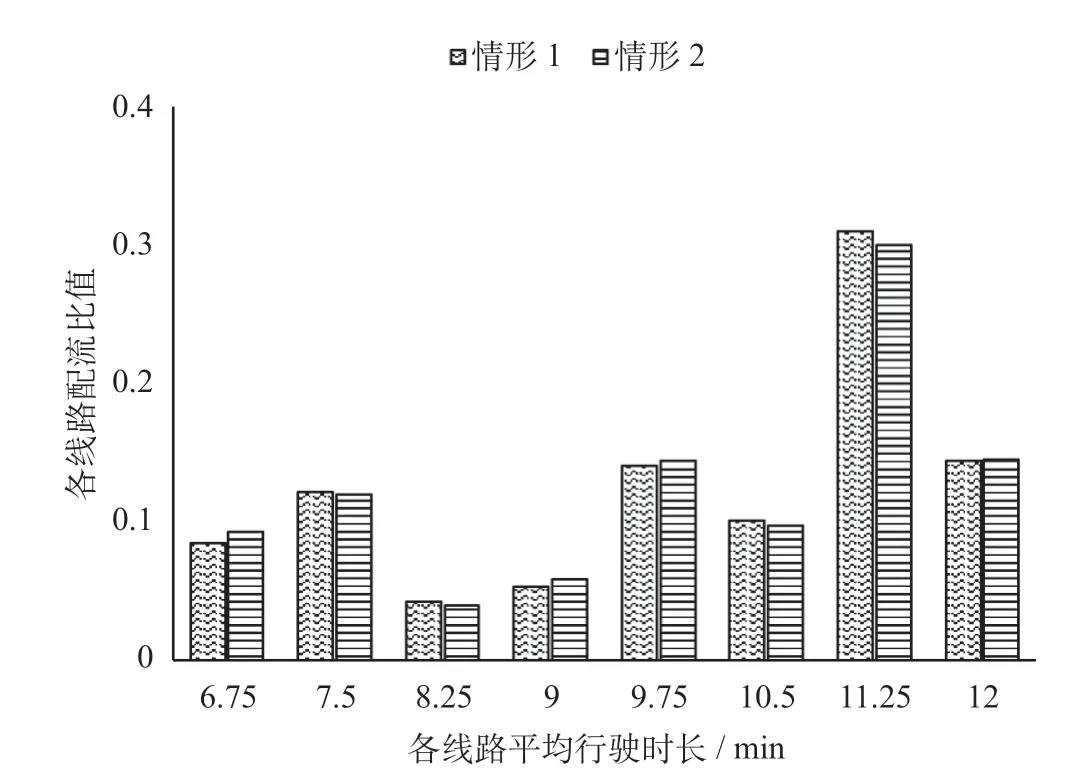
图4 各情形下各线路流量配比Fig.4 Flow ratio of each line in each case

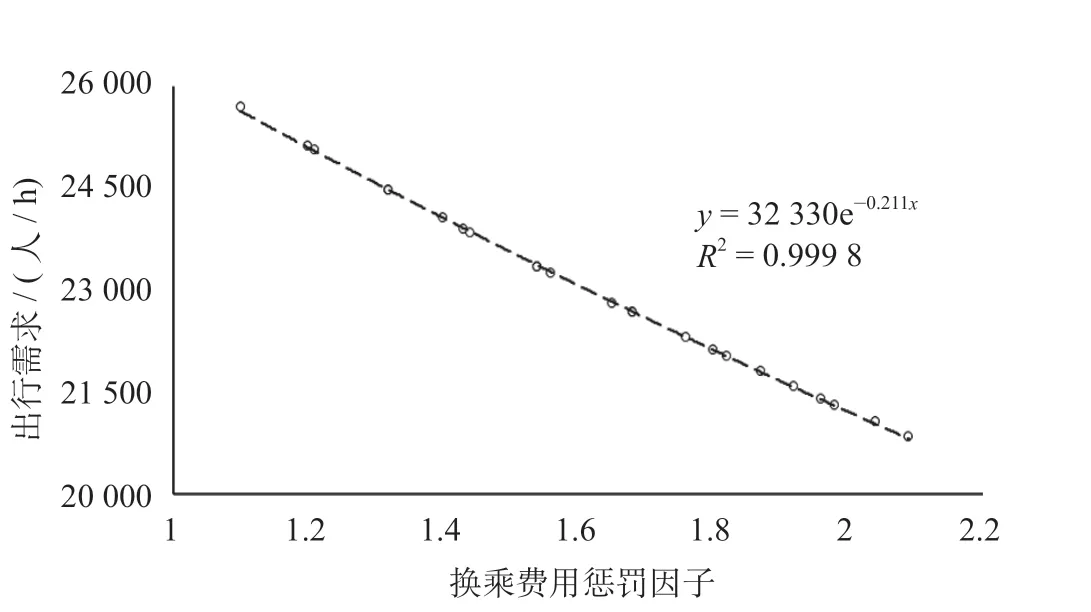
图5 换乘费用惩罚因子与出行需求的关系Fig.5 Relationship between the penalty factor for transfer and travel demand

图5 则显示以固定票价为前提，换乘费用惩罚因子与出行需求呈负相关；图6 显示以固定换乘费用惩罚因子为前提，出行需求与优化票价呈负相关；图7 显示换乘费用惩罚因子与优化票价呈现负相关，而换乘费用惩罚因子与出行需求呈正相关。弹性出行需求因票价的波动而产生变化，当换乘费用惩罚因子增大时，由于票价得到相应的下降，因而出行需求呈现上升趋势，即换乘费用惩罚因子与出行需求呈正相关。综合比较分析可知当换乘费用惩罚因子为定值时，出行需求随票价的降低而升高；当票价为定值时，出行需求随换乘费用惩罚因子升高而降低，这与图7 显示的优化票价下换乘费用惩罚因子与出行需求的关系相反，由此可知票价的优化对出行需求的影响作用大于换乘费用惩罚因子的影响。

换乘费用惩罚因子的增大导致换乘费用的提高、出行费用的增加，从而增加了乘客出行成本，减弱了乘客出行意愿。为达到既定的社会福利值，需通过降低票价实现出行成本的降低，以此抵消因换乘费用提高而增加的出行成本；通过拟合可知两者呈二次函数关系，由于换乘费用惩罚因子 ，结合二次函数对称轴单侧呈单调性的特点，因此换乘费用惩罚因子与最优票价呈负相关，当换乘费用惩罚因子以线性速度增加时，优化票价则呈加速下降趋势。

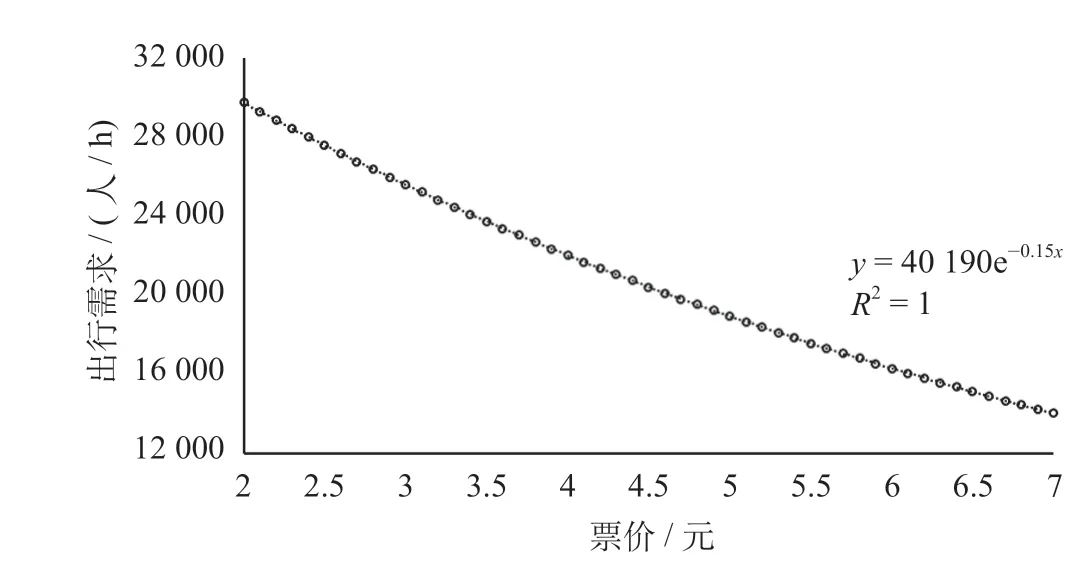
图6 票价与出行需求的关系Fig.6 Relationship between fare and travel demand

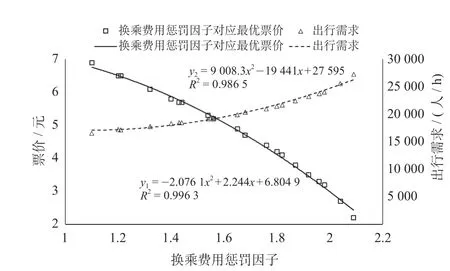
图7 换乘费用惩罚因子与出行需求、票价的关系Fig.7 Relationship between the penalty factor for transfer costs,travel demand, and fares

4 结束语

换乘费用对票价优化具有不可忽视的影响力，完善路网客流分配的影响参数，有利于实现票价的最优化。乘客倾向于选择换乘费用小，即换乘次数、等待时间较少的路线；随着换乘费用惩罚因子的提高，为达既定社会福利，需相应提升票价。但以乘客到站时间均匀分布、车间时距定值为假设计算等车时间，与实际情况存在一定偏差；模型中对多种时间进行统一量化，未考虑不同乘客对时间价值判断的差异性，上述不足将在下一步研究中加以剖析。