极限强度模型试验非线性相似方法研究

程瑞琪 朱思宇 邓 卉 裴志勇 吴卫国

(武汉理工大学交通学院1) 武汉 430063) (武汉理工大学高性能舰船技术教育部重点实验室2) 武汉 430063)

0 引 言

船体结构极限强度计算方法有直接计算法、Smith法、理想结构单元法、非线性有限元法和模型试验法等.直接计算法是在现有船舶数据基础上，假定船体梁受力状态来得到的，船型不同其适用性需要详细研讨，对于新船型或新的结构形式并不一定适用.Smith法建立在平断面假设的基础上，对于船舶弯曲状态下的极限强度，其计算精度相对较高，而对于扭转载荷作用其精度尚需进一步深入的研究和验证.理想结构单元法将材料非线性和几何非线性理想化并包括在单元中，从而可以将较大的几何单位视作一个理想结构单元，计算效率可大大提高.非线性有限元法可很好地模拟结构的屈服和屈曲等行为，为保证计算精度往往需要划分较细的网格，这给建模和计算工作带来了许多困难，对于诸如船体梁这类大型结构体系，建模工作量非常庞大、计算时间很长，往往在实际中难以实施.近年来，随着计算技术的发展，数值计算取得了长足的进步，但计算时间、计算结果精度都严重依赖于计算分析人员的技术积累和经验.有调查表明，针对同一结构，采用相同的边界条件和初始缺陷，不同研究者计算结果的差值能达到15%～20%[1].通过模型逐次崩溃试验，可以清楚、直观地了解船体结构在载荷作用下的破坏过程，揭示其极限承载能力.对新船型、新的结构型式，模型试验法是揭示船体结构崩溃机理和极限强度最根本、最有效的方法.总之，模型试验的研究方法在极限强度研究领域有着不可替代的作用[2].

在开展船体结构模型试验时，只有试验模型和实型之间保持一定的相似关系，才能根据模型试验结果推算至实船.师桂杰等[3]基于薄壁结构理论，对集装箱船船体结构弯曲相似和扭转相似模型展开研究，研究发现，在达到模型比例极限之前，两者均处于弹性状态，实船与模型的计算结果较为吻合，而超过弹性状态后两者相差较大.这是由于现有相似准则的推导基于弹性理论，仅能保证模型与实船在弹性范围内的相似性.为通过模型崩溃试验预报实船极限强度，既要确保试验模型与实船弹性阶段相似，同时也应满足非线性阶段结构行为的相似性.谢仲安[4]在理论分析的基础上，归纳总结了舱段模型极限强度试验的量纲分析方法，对相似准则进行了一些探讨，采用线性回归方法对模型试验结果预报实船极限强度进行了修正.该方法在线性范围内有着较高的精度，从物理意义上难以保证非线性预报的准确性.近年来诸多学者对结构非线性行为相似进行了探讨.Pei等[5]在设计某大开口江海直达船相似模型时，将板细长比和加强筋柔度系数等非线性因素考虑在内，使得试验模型和实型在压缩载荷作用下在线性阶段和非线性阶段均有相同的行为，从而可以通过模型试验结果预报实船结构的极限强度.该研究对加筋板承受压缩载荷作用的行为进行了研究，但并未探讨剪切载荷作用下的非线性行为.伍友军等[6]对双壳船体进行舱段相似模型设计，模型设计过程中综合考虑了众多非线性因素的影响，开展中垂极限强度试验，进行实船舱段与试验模型的中垂极限承载能力换算，预报实船舱段中垂极限承载能力.朱志辉[7]对加筋板在剪切作用下的非线性行为进行了初步探讨，提出以板剪切细长比表征其扭转非线性特性，据此设计了系列剪切相似模型，计算结果表明该系列模型与实型的剪切非线性行为存在着一些差异，需进一步深入、全面的研究.

本文将理论分析与数值计算相结合，首先对加筋板结构在剪切载荷作用下的逐次崩溃特性展开研究，确定影响加筋板剪切非线性行为的特征参数，提出试验模型与实船结构剪切非线性行为相似方法.基于所提出的非线性行为相似方法设计不同缩尺比的系列加筋板模型，对提出的剪切非线性行为相似方法进行初步验证.然后，以开发的宽扁型江海直达集装箱船为研究对象，设计相似模型，进行弯扭组合载荷作用下的极限强度模型试验，将模型试验结果推算至实船，进行极限强度预报，并将预报结果与实船有限元计算结果进行对比分析.提出的船体结构非线性行为相似方法，可使模型崩溃试验结果用于预报实船极限强度，对船体结构安全可靠性研究具有积极意义.

1 弯曲非线性行为相似方法研究

1.1 弯曲非线性行为相似方法

加筋板结构是组成船体梁的基本单位，其崩溃特性对船体梁的崩溃行为和极限强度有着重要影响.因此研究加筋板的崩溃特性是进行船体梁极限强度计算分析的基础[8].

通过对加筋板在压缩载荷作用下的崩溃特性研究表明，板细长比β可用来表征平板的逐次崩溃特性，柔度系数λ可用来表征加强筋的逐次崩溃特性.系列研究表明，对于不同尺度的加筋板结构，只要板细长比β和加强筋柔度系数λ相同，则它们在压缩载荷作用下的崩溃特性也基本相同，从而可根据相似比将模型试验结果推算至实船加筋板结构.

(1)

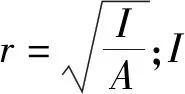
将上述船体结构弯曲非线性相似方法用以指导模型设计，使得试验模型的β和λ与实船结构相同，因此它们在弯曲载荷作用下的崩溃特性相同.

1.2 弯曲非线性相似方法验证

为验证船体结构弯曲非线性方法的有效性，设计了系列加筋板模型，各模型及原型的基本参数见表1.表中：No为加筋板编号；“N”为加筋板中板格数量，则加强筋数量为N-1；Ct为厚度缩尺比；CL为线尺度(长度、宽度)缩尺比；a，b，t分别为示板格长度、宽度和板厚，mm；hw、tw分别为加强筋中筋的腹板高度和厚度，mm；加强筋类型FB为扁钢.原型M0的结构形式见图1，有限元模型中纵骨间距间划分16个单元，长度方向96个单元，加强筋高度5个单元，有限元模型见图2.变化板长a，板宽b以及加强筋尺寸及数目，使得各试验模型的板细长比及加强筋的柔度系数均与原型的相关数值一致.各模型典型剖面特性见表2.表中：β为板格细长比；λ为加强筋柔度系数；A，I，r分别为单个加强筋的截面积、惯性矩、截面回转半径.

表1 计算加筋板基本参数(加强筋类型FB)

图1 加筋板结构

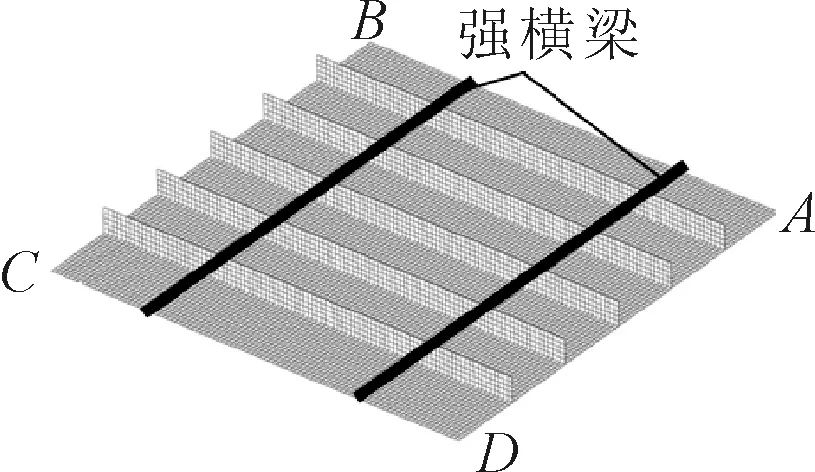
图2 有限元模型

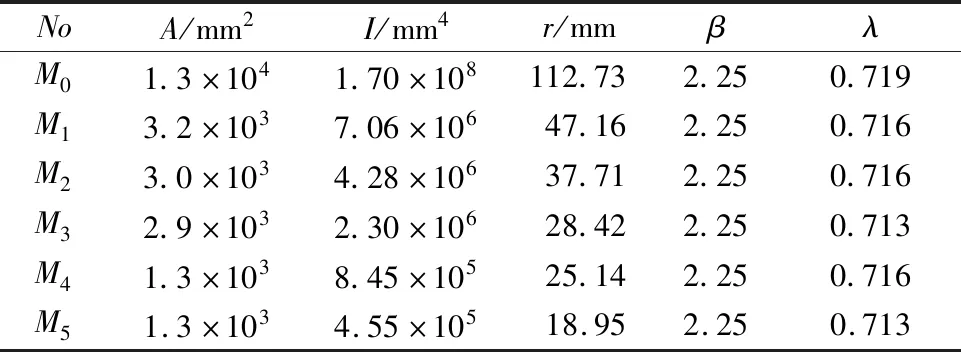
表2 各模型典型剖面特性

计算时在加筋板模型边界施加自由支持边界条件，强横梁处约束垂向自由度，AD边约束纵向、垂向平动自由度(Ux=0，Uz=0)及横向、垂向转动自由度(Ry=0，Rz=0)，BC边约束垂向平动自由度(Uz=0)及横向、垂向转动自由度(Ry=0，Rz=0)，AB边约束横向、垂向平动自由度(Uy=0，Uz=0)及垂向转动自由度(Rz=0)，CD约束垂向平动自由度(Uz=0)及垂向转动自由度(Rz=0).以强制位移的方式施加纵向压缩载荷，在BC边上施加纵向位移.

非线性有限元计算得到板格细长比和加强筋柔度系数相同的各加筋板模型在压缩载荷作用下的平均应力-平均应变关系曲线，见图3.板格细长比和加强筋柔度系数相同的各不同缩比加筋板的非线性特性基本一致，平均应力-平均应变关系曲线几乎相同.因此，将板细长比β和加强筋柔度系数λ作为船体结构纵向压缩载荷作用下的非线性特征参数是合理可行的，可以反映加筋板结构的逐次崩溃特征.

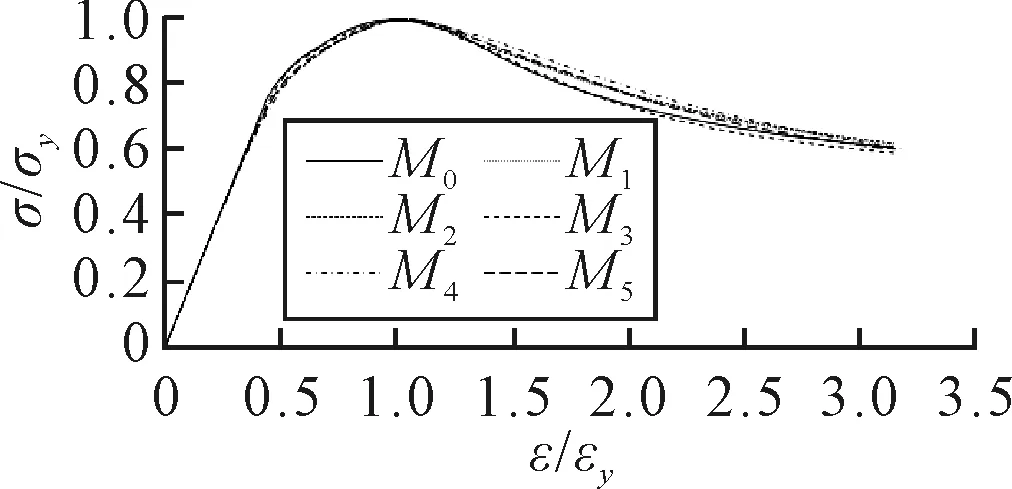
图3 各加筋板纵向压缩作用下平均应力-平均应变关系曲线

2 扭转非线性相似方法研究

2.1 扭转非线性相似方法

对加筋板结构在剪切作用下的逐次崩溃特性展开了研究.系列非线性有限元计算分析表明，在剪切载荷作用下，板的剪切细长比βτ对其崩溃特性起着重要作用，因此作者们提出采用板剪切细长比表征其非线性特征，即

(2)

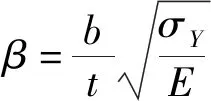
系列计算分析表明剪切柔度系数λτ对加强筋在剪切载荷作用下的逐次崩溃行为起着重要作用，因此采用加强筋剪切柔度系数λτ来表征其非线性特征，即

(3)

对于不同尺度的加筋板结构，只要板的剪切细长比βτ和加强筋的剪切柔度系数λτ相同，加筋板结构在剪切载荷作用下的崩溃行为基本相同，可用这两个参数表征加筋板结构剪切作用下的非线性特性.

2.2 扭转非线性相似方法验证

为验证船体结构扭转非线性方法的有效性，设计了系列加筋板模型，各模型及原型的基本参数见表3，表中各列参数的意义与表1相同.原型M0的结构形式见图4，有限元模型中纵骨间距间划分16个单元，长度方向48个单元，加强筋高度5个单元，有限元模型见图5.变化板长a，板宽b以及加强筋尺寸与数目，使得各试验模型的板剪切细长比βτ和加强筋的剪切柔度系数λτ均与原型的相关数值一致.各模型典型剖面特性见表4.

表3 系列加筋板基本参数(加强筋类型FB)

图4 加筋板结构

图5 有限元模型

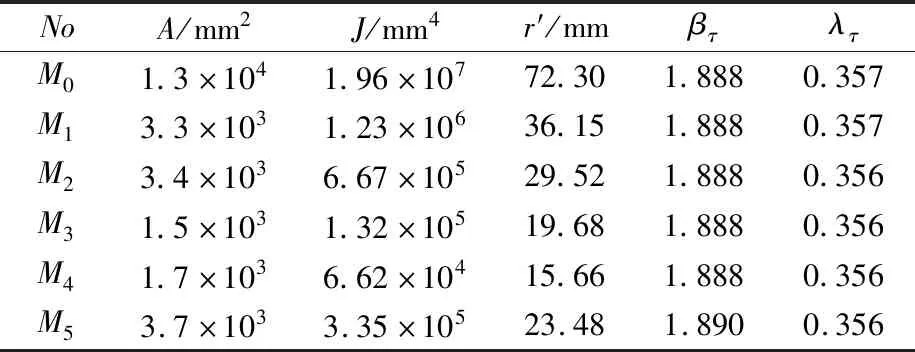
表4 各加筋板剖面特性

计算时在加筋板模型边界施加自由支持边界条件，AD边约束纵向、垂向平动自由度(Ux=0，Uz=0)及垂向转动自由度(Rz=0)，BC边约束垂向平动自由度(Uz=0)及垂向转动自由度(Rz=0)，AB边约束横向、垂向平动自由度(Uy=0，Uz=0)及垂向转动自由度(Rz=0)，CD约束垂向平动自由度(Uz=0)及垂向转动自由度(Rz=0).以强制位移的方式施加剪切载荷，在BC边上施加y方向的位移.

非线性有限元计算分析得到板剪切细长比βτ和加强筋的剪切柔度系数λτ相同的各加筋板模型在剪切载荷作用下的平均剪应力-平均剪应变关系曲线，见图6.板剪切细长比和加强筋剪切柔度系数相同的各不同缩比加筋板的剪切非线性特性基本一致，平均剪应力-平均剪应变关系曲线几乎相同.因此，将板剪切细长比βτ和加强筋剪切柔度系数λτ作为船体结构剪切载荷作用下的非线性特征参数是合理可行的，可以反映加筋板结构剪切载荷作用下的逐次崩溃特征.

图6 各加筋板剪切载荷作用下平均剪应力-平均剪应变关系曲线

3 弯扭组合载荷作用下船体梁极限强度

3.1 试验模型设计

以开发的宽扁型江海直达集装箱船为研究对象，基于线性相似准则和本文所提出的非线性相似方法设计相似模型，进行弯扭组合载荷作用下的船体结构模型崩溃试验.试验模型为三舱段模型，见图7.首尾舱段视为加载段，中间舱段为试验段.在首尾舱段的顶部施加自由支持的边界条件，在中间舱段横舱壁位置处船底板左右舷边施加载荷，通过调整左右舷载荷的大小，形成一定比例的垂向弯矩及转矩.试验过程中，左右舷载荷比例保持不变，在中部试验段形成一定的弯矩和转矩比值，逐步加大载荷值，直至试验模型破坏为止.

图7 试验模型示意图

试验模型的设计要能反映实船船体结构的逐次崩溃特性，且易于加工，易于加载.试验模型采用实船的船舯剖面型线进行线尺度相似设计，以加筋板为基本设计单位，基于线性相似准则和非线性相似方法进行模型设计.在满足线性相似准则条件的基础上，通过合理的选取模型中加强筋的间距以及尺寸，使得模型与实船中相应位置的加筋板结构具有相似的屈曲强度和失稳模式，尤其是船底板、舷侧板以及纵向贯穿构件等主要承力结构，要严格满足弯扭非线性相似方法的要求，尽可能使模型与实船在相应位置处的加筋板结构具有相同的细长比β、柔度系数λ、剪切细长比βτ以及剪切柔度系数λτ，从而保证模型与实船非线性阶段的相似性.

试验模型与实船的横剖面对比图见图8，在纵向弯曲载荷作用下，中和轴附近结构的应力水平较低，不会发生崩溃破坏，从加工的角度出发可适当简化相关结构，如实船设有两层平台甲板，在模型中将处于中和轴位置附近的那一层平台甲板省略.为便于加工，模型中所有构件均采用扁钢.且由于模型尺寸较小，可忽略减轻孔和尺寸较小的水平、垂直加强筋.

图8 模型与实船横剖面对比

为验证试验模型设计的合理性，对模型与原型的中横剖面特征参数进行了对比分析，中和轴位置、剖面积、惯性矩、剪心位置、自由扭转惯性矩和约束扭转惯性矩等见表5，试验模型与原型的各项横剖面特征参数基本相同，最大相对误差为4.42%，从而说明所设计的试验模型能较好的反映实船结构的基本特征，是合理可行的.

表5 试验模型和实船横剖面特征参数对比表

3.2 实船有限元分析

全船计算模型采取三舱段模型，取实船的中间舱室然后分别向船艏、船艉延伸一个舱室，得到全船计算模型，见图9，首尾部分作为边界条件的施加位置，在结构上进行了加强以避免破坏.通过非线性有限元软件Abaqus，采用动态显示算法计算全船模型在弯扭组合载荷作用下的极限强度.采用O-XYZ直角坐标系，X轴正向指向船艏，Y轴正向指向左舷，Z轴正向指向甲板.为更好地模拟实际情况和得到更精确的计算结果，有限元模型中所有单元均为板单元.由于两端为延伸段，并不是主要研究对象，为提高计算速度和计算精度，仅对中间段的网格进行了细化，细化部分沿船长方向长度为11 900 mm.延伸段的纵骨间距划分1个网格，而中间段的纵骨间距划分六个网格；延伸段的纵骨高度方向划分一个网格，而中间段的纵骨高度方向划分四个网格；延伸段的横框架间距划分三个网格，而中间段的横框架间距划分18个网格.

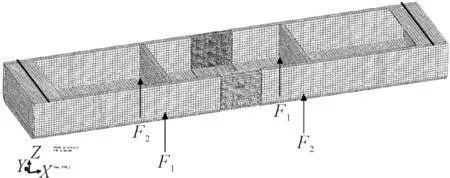
图9 全船计算模型

为了更好地将有限元计算结果与模型试验结果进行对比分析，在有限元计算中模拟的边界条件与加载方式均与模型试验一致.计算中模拟的边界条件为：在船艏顶部一列节点处约束纵向、横向、垂向平动自由度(Ux=0，Uy=0，Uz=0)及纵向、垂向转动自由度(Rx=0，Rz=0)，在船艉顶部一列节点处约束横向、垂向平动自由度(Uy=0，Uz=0)及纵向、垂向转动自由度(Rx=0，Rz=0).计算中模拟的加载方式为：在中间舱段横舱壁位置处船底板左右舷边设有四处加载点，通过设置左右舷载荷的大小，形成与模型试验具有相同比例的垂向弯矩及转矩.计算得到实船极限弯矩为8.421×1011N·mm，实船极限转矩为8.587×1010N·mm .

3.3 实船极限强度预报

基于相似理论可知，弯矩和转矩的相似比应为：CM=CT=C2LCt.即可通过下式由模型试验结果预报实船极限弯转矩.

Ms=Mm·CM=Mm·C2LCt

(4)

Ts=Tm·CT=Tm·C2LCt

(5)

式中:Mm为试验模型弯矩；Tm为试验模型转矩；Ms为模型试验预测实船弯矩；Ts为模型试验预测实船转矩.

通过模型试验可以得到模型所受弯矩、转矩，根据式(4)～(5)可以由模型试验结果推算出实船弯矩、转矩.

选取右舷侧下方靠近船艏处加载点的位移(模型试验与有限元计算所选取位移点位置一致)作为横坐标，对比分析模型试验预测弯矩、转矩-位移曲线与全船模型有限元计算所得弯矩、转矩-位移曲线，见图10.

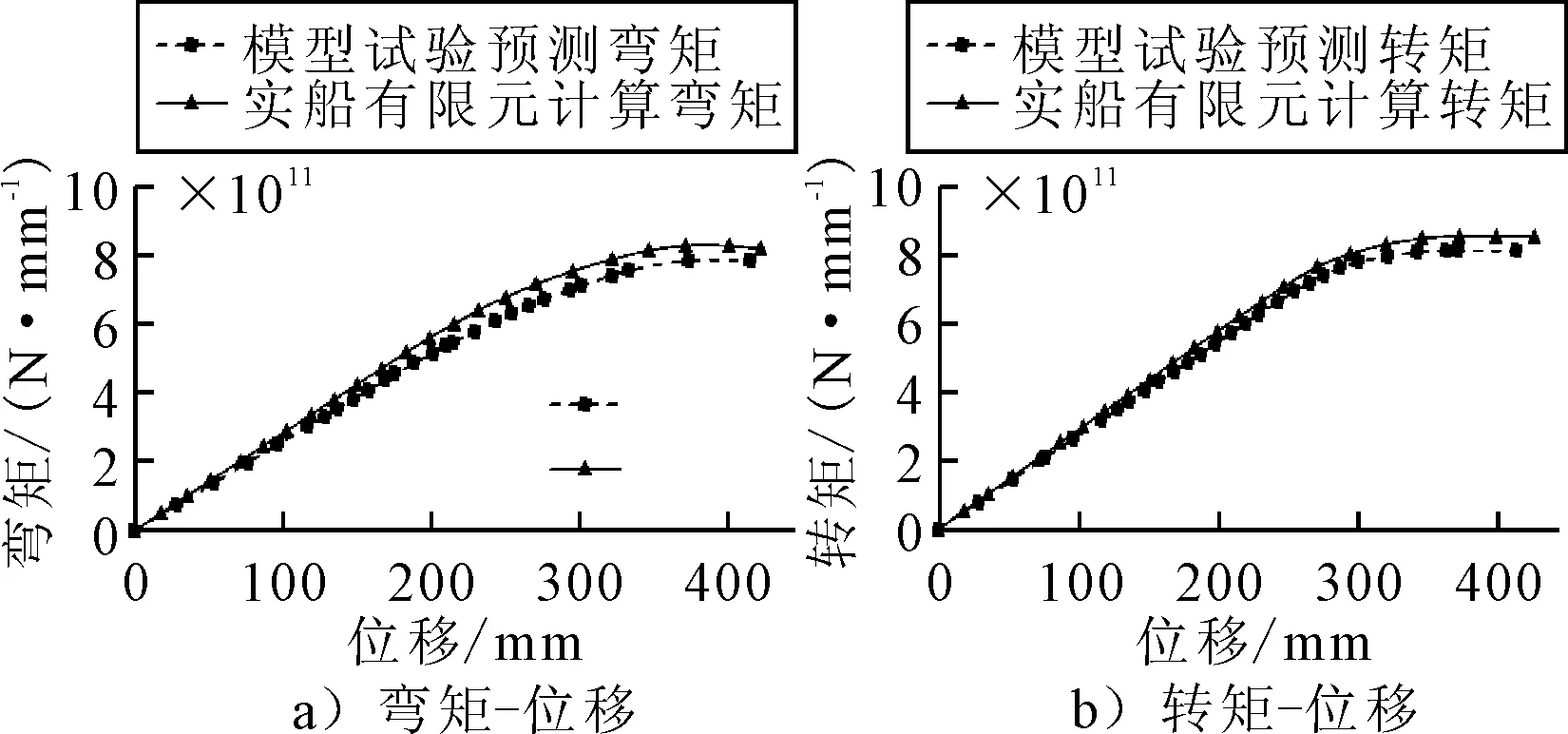
图10 弯矩和转矩与位移曲线

由图10可知，根据模型试验结果预测所得实船弯矩、转矩-位移曲线与实船有限元计算所得弯矩、转矩-位移曲线在线性阶段几乎完全重合，在非线性阶段亦基本保持一致.模型试验所得极限弯转矩、预测所得实船弯转矩和有限元计算所得实船极限弯转矩见表6.

表6 极限强度对比表

由表6可知，通过模型试验预测所得实船极限弯矩与有限元计算所得实船极限弯矩相差5.501%，通过模型试验预测所得实船极限转矩与有限元计算所得实船极限转矩相差4.987%.由于在数值仿真计算中没有考虑到焊接残余应力和初始缺陷的影响，所以计算结果相较于实际情况是偏大的.因此，可以认为通过模型试验预测所得实船极限强度与计算所得实船极限强度是一致的.

通过对模型试验结果与数值计算结果的对比分析，证明了本文所提出的非线性相似方法可以保证模型与原型在非线性阶段的相似性.基于非线性相似方法设计所得的试验模型可以用来进行极限强度模型试验，并且可以通过试验结果来预测实船极限强度.

4 结 论

1) 板细长比β和加强筋柔度系数λ是加筋板轴向压缩载荷作用下的重要参数，在设计相似模型时保证模型与原型的β及λ相等，可使模型与原型具有相似的轴压载荷作用非线性行为.

2) 板剪切细长比βτ和加强筋剪切柔度系数λτ是加筋板剪切载荷作用下的重要参数，在设计相似模型时保证模型与原型的βτ及λτ相等，可使模型与原型具有相似的剪切载荷作用非线性行为.

3) 基于本文所提轴压载荷作用非线性相似和剪切载荷作用非线性相似方法来设计试验模型，模型在弯扭载荷作用下的逐次崩溃行为与实船相应的非线性行为相似，可通过模型试验结果预报实船的极限强度；

本文所提出的非线性相似方法是对现有模型相似理论的补充和完善，弥补了现有线性相似理论的不足.