多车辆移动荷载和桥梁耦合振动的参数分析*
王 娟 张迎春 钱 江
(上海建桥学院商学院1) 上海 201306) (同济大学土木工程防灾国家重点实验室2) 上海 20092)
0 引 言
车桥耦合振动的计算模型的差别主要在于车辆的简化模型.车辆的简化模型从简单到复杂可分为四种类型:移动荷载、移动质量、单轴弹簧-阻尼-质量系统、多轴弹簧-阻尼-质量系统[1].Fryba[2]给出了不同车辆模型的控制方程及求解方法.肖新标等[3]对比了三种车辆模型作用下桥梁的动态响应.随着研究不断深入,车辆模型从一车模型发展到多车模型[4-5],并且车桥耦合振动中的共振现象也引起了学者的关注.Yang等[6]以间距为列车长度的移动质量模拟列车荷载,并给出与车辆速度引起桥梁共振和消振的条件.李小珍等[7]建立了任意移动弹簧-阻尼-质量列模型作为多车辆荷载,分析了车速对桥梁响应的影响.李慧乐等[8]以移动荷载列为车模型给出简支梁发生共振及两类消振效应(单荷载和荷载间距)的车速计算公式,并指出消振与荷载间距有关.Yang等[9-10]进一步研究了车辆和桥梁共振的机理.Yang等[11]通过简单的弹簧质量车模型和复杂的多体车模型分析验证了一定跨度的连续桥梁引起列车共振的条件,以及车辆作用引起桥梁共振的条件.
目前,多车荷载的研究主要集中在车辆速度以及车辆间距和桥跨长度对桥梁动态响应的影响,车辆和桥梁的其他参数对系统响应的影响并没有全面展开.而且过于简单的荷载列模型不能真实的反应车桥耦合的振动效应,复杂车模型作为荷载激励也不易在桥梁设计中推广.鉴于此,文中选择单轴弹簧-阻尼-质量系统为车辆模型进行多车荷载激励的研究.桥梁简化为简支的欧拉梁,通过MATLAB编程计算,全面揭示桥梁和车辆参数变化的影响.主要内容如下:①对比现有文献的计算结果,验证一车和多车荷载的车桥耦合振动模型.②选择跨长30 m桥梁在双车或多车荷载作用下进行参数分析.选择参数如下:车辆速度、车辆间距、车辆轮胎和悬架质量比、车-桥质量比、车辆刚度、车辆和桥梁阻尼特性,以及车辆轴数.
1 两辆或多辆车运行下的车桥耦合振动计算模型
根据文献[2]单轴弹簧-阻尼-系统建立一辆车的车桥耦合振动模型,推广到多辆车激励的控制方程.在实际工程中两辆车或多辆车连续通过桥梁的情形非常普遍,对于桥梁的动态响应而言,多辆车激励的响应并不等同于多个一个辆车激励的响应叠加.两辆车的车桥耦合振动计算模型见图1.

图1 两辆车与桥梁耦合振动的计算模型
相应的控制方程为
(1)
(2)
(3)
式中:yi为第i辆车悬架竖向位移;mi1和mi2分别为车轮轮胎和车辆悬架质量;t为车辆运行时间,从车辆接触桥梁开始计算;y(x,t)为t时刻x处的桥梁竖向位移;E为桥梁的弹性模量;I为桥梁截面的惯性矩;μ为桥梁的线密度;c为桥梁的黏性阻尼系数,假定为Rayleigh阻尼;δ(x)为狄拉克函数;ki和ci分别为车辆刚度和阻尼系数;v为车辆运行速度;Pi=(mi1+mi2)g;s为车辆间距.文中忽略桥面粗糙度.
M辆车的车桥耦合振动的控制方程由M+1个方程组成,前M个方程是M辆车的控制方程,其中第M个、第M+1个方程是桥梁的控制方程为
(4)
(5)
y(x,t)可以采用模态位移改写为
(6)

(7)
式中
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
{y}={y1,y2,…,yM}T
(18)
{T}={T1,T2,…,TN}T
(19)
P={∑M1PiY1i/L,∑M1PiY2i/L,…,∑M1PiYNi/L}T
(20)
式(7)~(20)采用Newmarkβ法进行编程求解.
2 车辆与桥梁耦合振动计算模型的验证
模型验证分为两个方面:一车耦合振动模型和多车耦合振动模型的验证.选择Xiang等[12]算例验证一车和多车计算模型.计算模型参数如下.μ=2.303×103kg/m,m11=0,m12=5 750 kg,k1=1.595×106N/m,c1=0,E=2.87 GPa,I=2.9 m4,桥梁的基频为20.85 rad/s,桥梁的跨度为30 m,车辆速度为27.78 m/s.图2为桥梁跨中竖向位移和悬架质量m11竖向位移的对比,由图2可知,数值结果吻合良好,因而计算模型对于一辆车的荷载激励是可靠的.

图2 竖向位移时程
目前为止未见质量-弹簧-阻尼系统的多辆车算例的文献,因而设定mi1,ki1,ci1为0,把多车辆模型退化为连续集中力与文献[6]的算例进行对比验证.算例中5车辆10个连续集中荷载以速度26和34 m/s通过桥,两个速度分别对应消振和共振工况.模型数据为:μ=3.408 8×104kg/m,E=29.43 GPa,I=3.81 m4,桥梁的跨度为20 m,桥梁的基频为44.75 rad/s,轮胎质量为22 000 kg.得出两个速度工况的桥梁跨中位移和不同速度对应的最大位移见图3~4.图3结果表明,26 m/s的工况位移时程曲线的幅值和相位非常吻合.34 m/s的工况在曲线的局部峰值与文献结果略有差异,但极值和相位均非常接近,文献[6]的位移极值分别为0.32和-0.93 mm,文中的极值分别为0.33和-0.93 mm.图4结果表明,计算结果非常接近,文中曲线最大值为3.69 mm,文献[6]的最大值为3.66 mm,对应的速度无量纲参数S1相同.因而多车辆荷载的退化模型仍然是可靠的.通过一车辆模型和连续荷载列模型的算例验证了本文计算模型的可靠性.

图3 桥梁跨中时程响应

图4 响应幅值与速度参数S1
3 两辆车运行下的中等跨度桥梁的参数分析


表1 车桥耦合振动计算模型的参数
引入动力放大系数DAL,研究桥梁的最大位移和特定参数之间的关系,计算公式为
DAL=δdyn/δsta
(21)
式中:δdyn为桥梁的最大动态响应;δsta为桥梁的最大静态响应.一车模型作用下桥梁的最大静态位移是车辆位于跨中引起的跨中静态位移,相同间距的两车或多车作用下桥梁最大静态位移是车辆以跨中为中心,对称分布于桥梁引起的跨中位移.
3.1 车辆速度的影响
多个车辆均采用相同模型,车辆速度从4 m/s增加到240 m/s,每次增加1 m/s.车辆间距均相等.车辆间距s=8 m的多个车辆运行下桥梁的动力放大系数与一车激励的对比见图5.由图5可知,不同数量车辆的动力放大系数均有随速度增加而增长的趋势,最大峰值有降低的趋势,与最大峰值和局部峰值相应的速度有增大的趋势.在特定的速度区间(比如80~150 m/s),速度不变的情况下,动力放大系数随车辆数量降低,说明车辆的增加导致最大动态位移增长的速度小于最大静态位移增长速度.对于桥梁工程师而言,需考虑多车辆运行的动力放大系数与一车的差异.
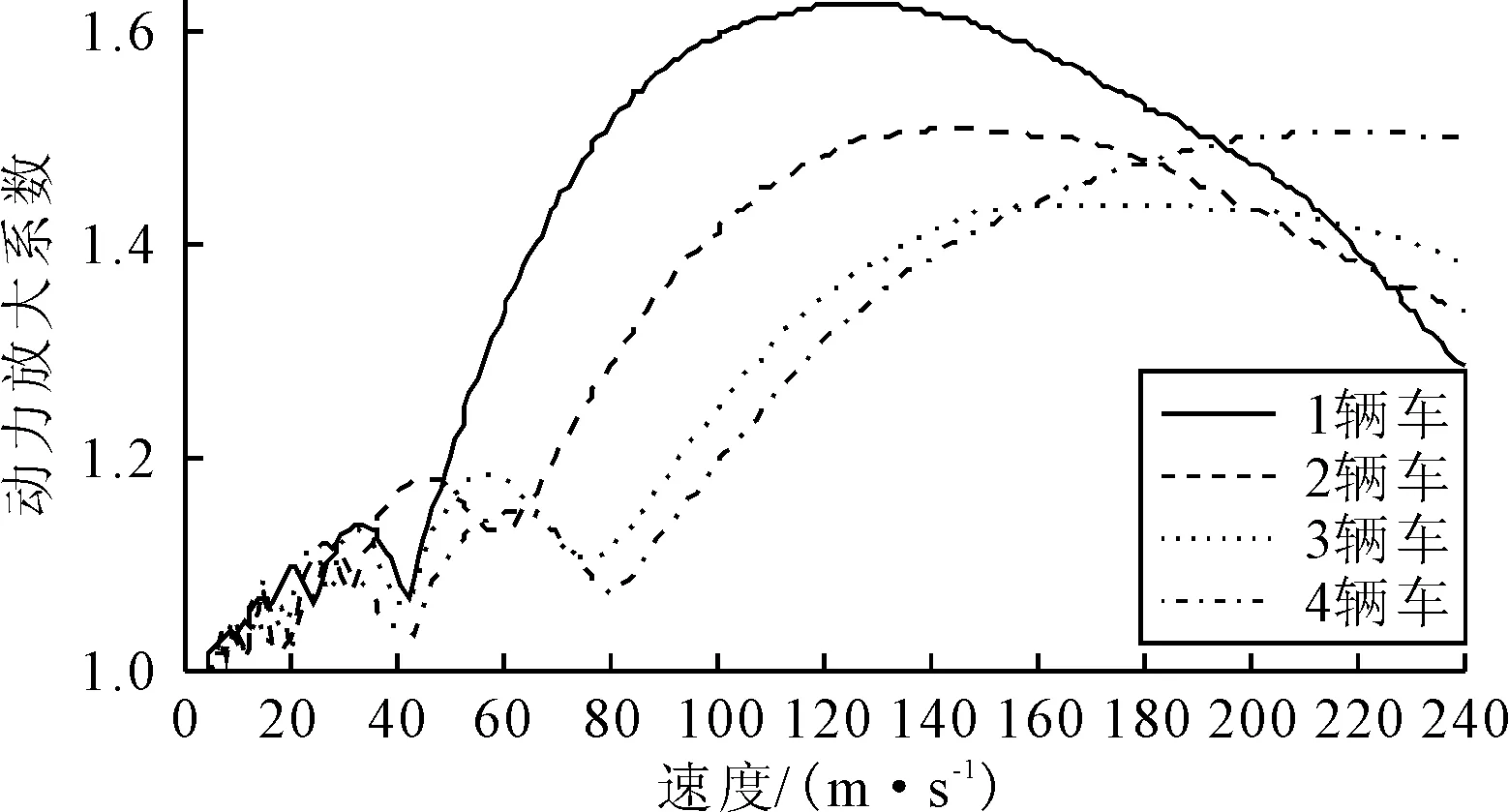
图5 桥梁动力放大系数与速度(s=8 m)
文献[6]给出了连续荷载列引起桥梁共振的速度公式为
v=sω1/2iπ (i=1,2,…)
(22)
式中:s为车辆间距;ω1为桥梁第一自然圆频率,此公式适用于桥梁跨度不超过车辆间距的2倍,即s≥L/2.图6为间距s=26 m的3~6辆车作用下的桥梁动力放大系数的对比.由图6可知,不同数量车辆的动力放大系数曲线相位几乎一致,只在接近局部峰值的范围内幅值有差异.这是因为随着车辆的增多延长了桥梁振动的时程,桥梁共振位移随时间而增长,导致峰值的增加.表2为2~7 辆车连续通过引起的位移峰值对应的速度和动力放大系数.由表2可知,随着车辆增加,局部峰值对应的速度逐渐接近文献[6]的公式得出的共振速度,直到车辆增加到7辆,峰值对应的速度不再变化.实际上共振速度不仅限于式(22)给出的速度,在接近局部峰值速度的范围内同样具有共振效应.图7为3辆车间距s=26 m在速度83,93,103 m/s的桥梁跨中位移时程曲线,除了峰值对应的速度93 m/s之外,83和103 m/s的速度工况同样显示出位移随时间增长的共振效应.对于动力放大系数的曲线波段而言,从离开波谷速度63 m/s,从64 m/s开始就出现共振效应,到波峰对应的93 m/s共振效应最大,直到111 m/s之后共振效应不再明显.因而峰值附近的速度工况产生的位移放大效应同样值得桥梁设计师注意.

图6 桥梁动力放大系数与速度(s=26 m)
3.2 车辆间距的影响
观察恒定速度下车辆间距s变化影响桥梁动态响应的规律.选择两车模型进行研究,车辆间距0.5~29.5,每次增加0.5 m,选择三个速度工况进行对比,分别为20,60,100 m/s.由于车辆间距29.5 m工况下桥梁最大静态位移为0.19 mm,得出的动力放大系数远远大于间距较小的工况,因而选择跨中最大动态位移进行观察,计算结果见图8.由图8可知,桥梁位移响应并未呈现单调变化趋势.对于20 m/s(72 km/h)的工况,当间距大于19 m(s/L>0.63)时跨中最大位移明显降低;对于60 m/s(216 km/h)的工况,当间距在19~24 m(s/L在0.63~0.8)时跨中最大位移明显降低;对于100 m/s(360 km/h)的工况,当间距在16~22 m(s/L在0.53~0.73)时跨中位移明显降低.不同速度工况表现出在间距和桥跨比为0.6左右的位移较小.因而可以利用这个特点,选择适当的桥梁跨度或车辆间距来设计桥梁或交通.

表2 不同数量车辆的共振速度和动力放大系数DAL(s=26 m)

图7 3车模型的桥梁跨中位移时程(s=26 m)

图8 车辆间距变化对桥梁位移响应的影响
车辆间距和速度的变化对桥梁动态响应的影响可以绘制成云图.图9分别显示了2~4辆车作用下桥梁的跨中最大动态位移的变化规律.可以观察到特定间距下速度变化对跨中位移的影响,也可以观察特定速度下车辆间距的变化对跨中位移的影响.这3张图跨中位移的变化规律具有相似的变化趋势,例如,3张图均具有左上角跨中位移较小的特点,说明当速度小于40 m/s,车辆间距大于15 m(s/L>0.5),桥梁跨中位移较小.云图显示速度越大、间距越小桥梁响应越大,但是当速度在90~110 m/s,车辆间距接近桥跨,尽管静态位移较小,造成的动态位移仍然很大.

图9 2~4辆车通行时桥梁最大跨中位移云图
3.3 车辆质量变化的影响(mi1/mi2)
车辆质量的变化从两个方面考察,一个是车辆轮胎和悬架质量比(mi1/mi2)的变化,另一个是车辆总质量与桥梁质量比(mi2/(μL))的变化.保持mi2不变,增大mi1的质量,mi1/mi2的变化范围在0%~15%.动力放大系数的变化与速度有关,图10为速度为20,60,100 m/s的两车模型、车辆间距s=10 m的动力放大系数,三条曲线均呈现单调变化趋势,其中20和60 m/s的工况动力放大系数随质量比的增加呈减小的趋势,而100 m/s的工况正相反,呈增加的趋势.桥梁的动态和静态响应均随车辆质量的增加而增加,但不同速度工况动态和静态响应的增长速度不同,导致动力放大系数变化趋势有差异.变化幅度比较小,因而悬架质量不变的情况下,车辆轮胎质量的变化对桥梁动力放大系数的影响不大.
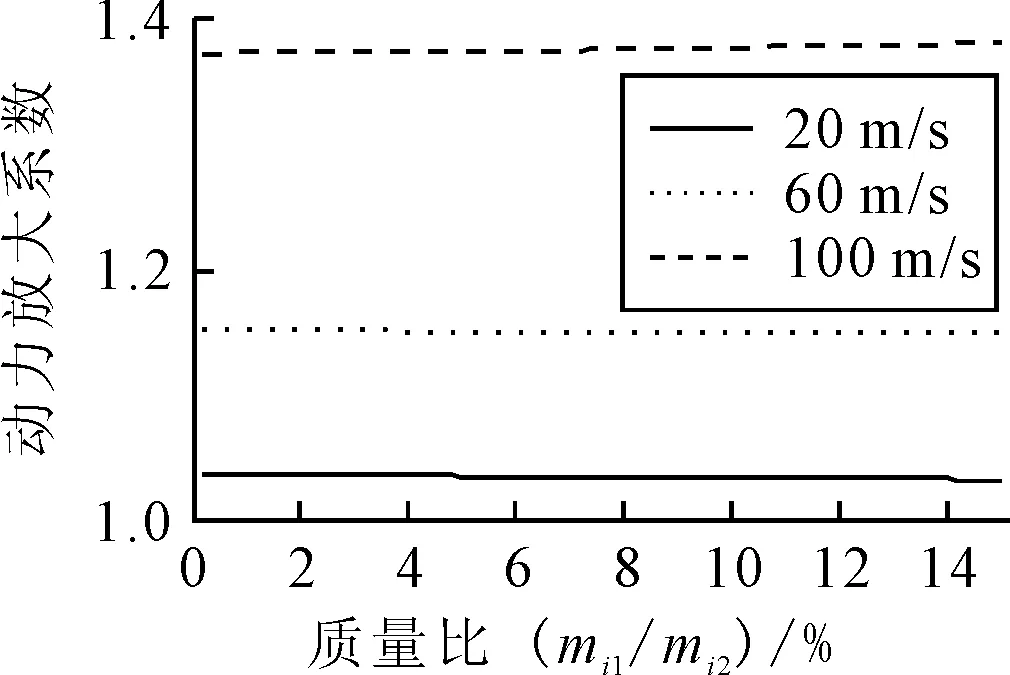
图10 动力放大系数与车辆轮胎和悬架质量比(s=10 m)
保持mi1不变,增大mi2的质量,mi2/(μL)的变化范围在0.2%~15%,即2辆车总质量与桥梁的质量比的范围在0.4%~30%.得出的动力放大系数见图11,由图1可知,三个速度工况对应的动力放大系数变化规律均不同,没有呈现单调的变化趋势.20 m/s的工况动力放大系数在质量比为8.4%时达到最小值1.01,质量比为30%时达到最大值1.09.60 m/s的工况动力放大系数在质量比为12%时达到最大值1.15.100 m/s的工况动力放大系数在质量比为1.6%时达到最大值1.52,在质量比为30%时达到最小值1.33.不论单独增加轮胎质量还是悬架质量,桥梁的跨中动态位移均呈现单调增加的形式,但动力放大系数与速度有关,而且车辆悬架质量的变化比轮胎质量的变化对动力放大系数影响更大.

图11 动力放大系数与车辆总质量和桥梁质量比(s=10 m)
3.4 车辆弹簧刚度变化的影响
车辆弹簧刚度ki的变化步长为50 kN/m,变化范围为800~2 400 kN/m,这两个限值是文献[12]算例模型刚度的50%和150%.图12为两车模型、车辆间距s=10 m的速度和车辆刚度与动力放大系数的关系云图.由图12可知,同样的速度,动力放大系数可能随刚度增加也可能减小,或者呈现非单调的曲线变化趋势.例如20和100 m/s的工况动力放大系数随刚度的增加而减小,而60 m/s的工况呈增加的趋势.20 m/s的速度工况动力放大系数从1.08降低到1.02,60 m/s的速度工况从1.06增涨到1.19,100 m/s的速度工况从1.41降低到1.36.尽管车辆刚度的变化对桥梁动态响应的影响与速度有关,但变化幅度并不显著.

图12 动力放大系数与车辆刚度和速度的变化云图
3.5 车辆阻尼的影响
车辆阻尼从0 N·s/m增加到19.1 kN·s/m,对应阻尼比范围0%~10%,增加步长为200 N·s/m.图13为速度为20,60,100 m/s的两车模型车辆间距s=10 m的动力放大系数,三条曲线均呈现单调变化趋势,其中20和60 m/s的工况动力放大系数随刚度的增加而减小,而100 m/s的工况正相反,呈增加的趋势.说明车辆阻尼的增加并不必然导致桥梁响应降低.速度大于65 m/s的动力放大系数开始呈现随阻尼增加而增加的趋势,速度大于150 m/s的动力放大系数开始呈现凹曲线形式.尽管不同速度的动力放大系数曲线变化趋势不同,变化幅度均不显著.20 m/s的速度工况动力放大系数从1.03降低到1.02,60 m/s的速度工况动力放大系数从1.15降低到1.13,100 m/s的速度工况动力放大系数从1.37增涨到1.39.因而动力放大系数对车辆阻尼的敏感性较低.

图13 动力放大系数与车辆阻尼
3.6 桥梁阻尼的影响
桥梁阻尼比从0增加到10%,图14为速度为20,60,100 m/s的两车模型在间距s=10 m的动力放大系数与阻尼比的关系,20 m/s和100 m/s的工况动力放大系数随阻尼比的增加而减小,20 m/s的速度工况动力放大系数从1.04下降到1.02,100 m/s的速度工况动力放大系数从1.37下降到1.31.而60 m/s的动力放大系数保持在1.15.图15为不同阻尼比的动力放大系数与速度关系,事实上在61~72 m/s之间动力放大系数随阻尼比的增加而增涨,这个区间也在消振速度区间,其他速度工况动力放大系数均随阻尼比的增加而减小.图16为65 m/s的工况在不同阻尼比下的跨中位移时程,由图16可知,在阻尼为0,0.025,0.05对应的最大动态位移分别为7.28,7.33和7.36 mm,尽管位移随阻尼比增大,但差异非常小.桥梁阻尼比的增大在某些消振速度工况不能起到减小振幅的现象在文献[6]中也同样出现,只不过作者并没有解释.粘滞阻尼对于减小共振峰值的作用非常明显.
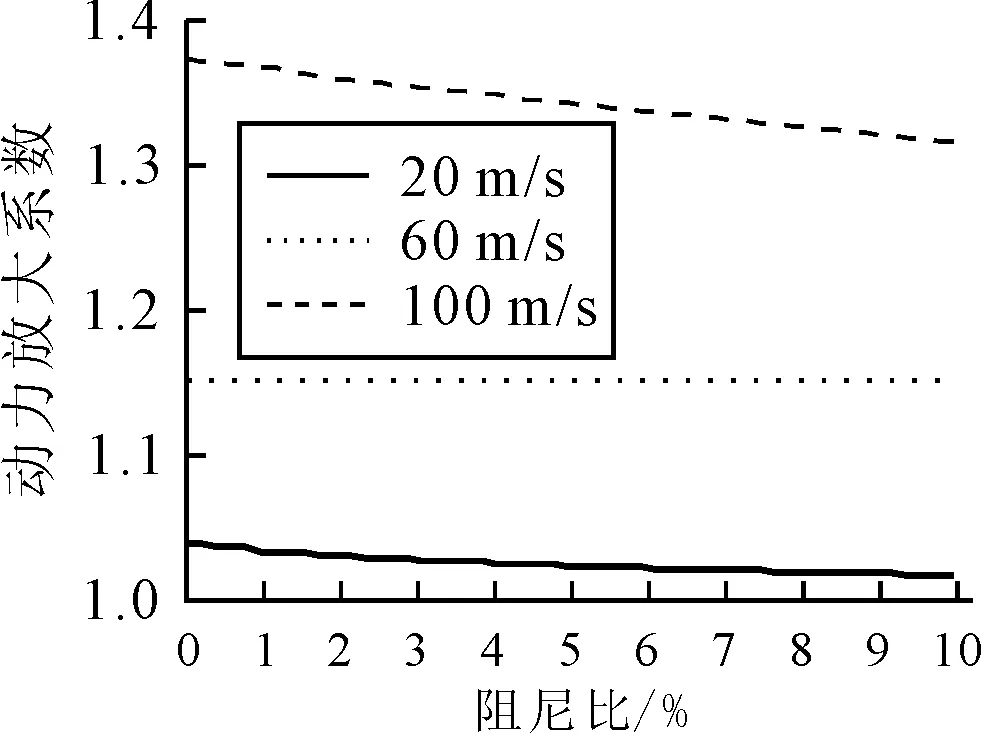
图14 动力放大系数与阻尼比(s=10 m)

图15 不同阻尼比的动力放大系数与速度关系
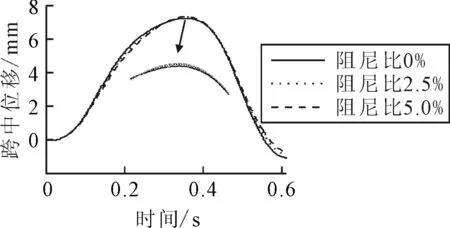
图16 不同阻尼比的跨中位移-时程(v=65 m/s)
3.7 单轴车辆与双轴车辆的比较
前面的计算结果均采用单轴车辆模型,采用双轴或多轴车辆模型更接近实际工程.本节把单轴车辆的质量和刚度减半,使双轴车辆的质量和刚度与单轴车辆相等.采用轴距2 m,车辆间距为s=26 m,与同样间距的单轴车辆比较.图17为4辆车单轴和双轴模型的动力放大系数(7辆车的对比曲线与4辆车的曲线有相似的变化趋势).由图17可知,双轴车辆与单轴车辆的动力放大系数在25 m/s以上的速度工况比较吻合,捕捉到的峰值点对应的速度也一致,11~19 m/s动力响应差异较大,4车模型单轴响应与双轴响应最大差异33%,7车模型最大差异30%.因而对于城市交通限速20 m/s以下的桥梁采用双轴车辆计算更加合理.
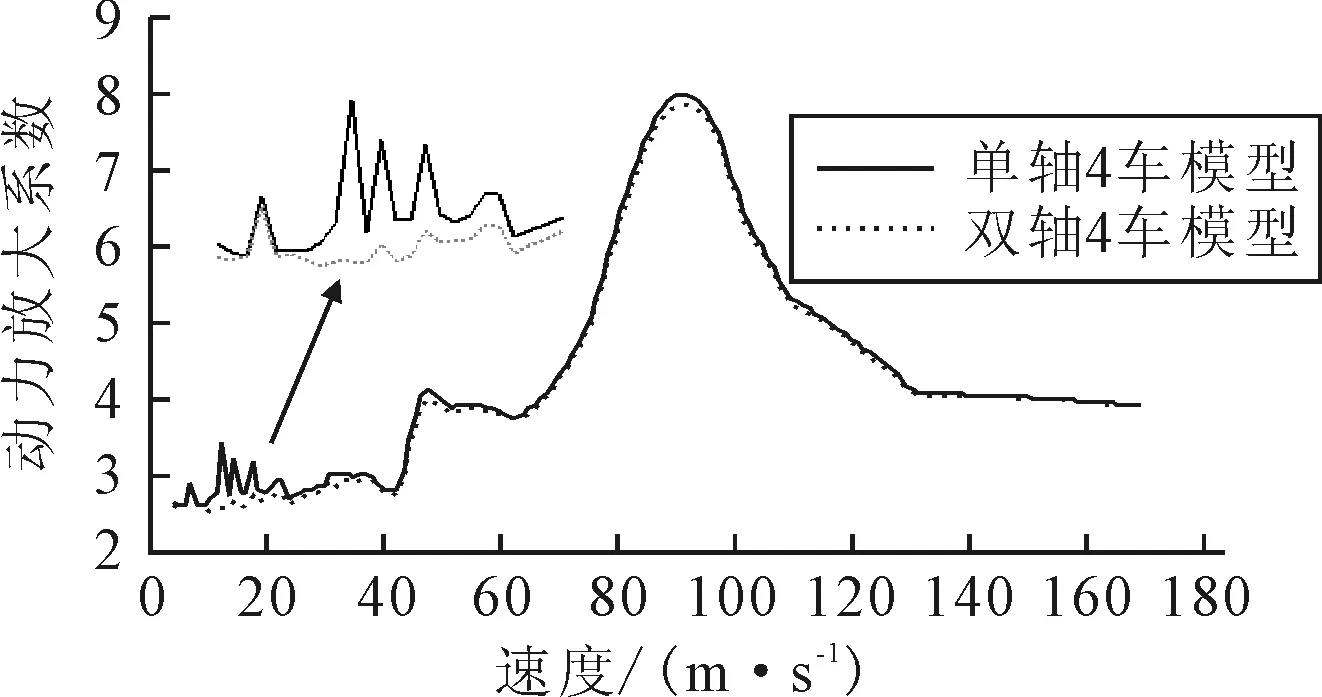
图17 单轴和双轴4辆车的动力放大系数(s=26 m)
4 结 论
1) 车辆速度对桥梁的动态响应影响较大,一辆车或连续车辆的移动荷载都会引起桥梁的共振效应,除了响应峰值相应的共振速度,也需要注意共振速度附近的位移放大效应.
2) 车辆间距的变化对桥梁动态响应也很显著.由于间距接近桥跨长度静态位移很小,造成动力放大系数很大,桥梁设计不仅需要参考动力放大系数,同时也想需要参照动态响应.车辆间距小于1/2桥跨时桥梁的动态响应随间距增加而减小,在间距与桥跨比值0.6附近响应最小,这个特点可以作为桥梁或交通设计的参考.
3) 增加车辆的轮胎质量和悬架质量都会引起桥梁动态响应的增大,但动力放大系数的变化与速度有关,有些速度工况下动力放大系数呈下降趋势,总体来说差异不大.车辆悬架质量的变化比轮胎质量的变化对动力放大系数影响更大.
4) 尽管车辆刚度的增加导致桥梁的动态响应因速度而不同,可能增加也可能降低,或呈现非单调的曲线变化规律,但变化幅度并不显著.
5) 车辆的阻尼对桥梁响应的敏感性较低,但是桥梁的阻尼具有明显的降低共振振幅的作用.
6) 双轴和单轴的简化车辆模型的分析表明:双轴车辆模型对低速(11~19 m/s)的工况影响更大,其他速度工况与单轴车辆模型差异较小.
总之,桥梁和车辆的参数中车辆速度和车间距与桥跨比值对桥梁动态响应具有显著影响,车辆总质量和刚度的变化对桥梁响应的影响随速度而不同,可以利用参数变化的规律设计桥梁和交通.

