岩土工程安全监测交叉影响分析的原理及应用*
郭运华 吴 昊 姜永涛 王正庆 高小雷 李玉祥
(武汉理工大学道路桥梁与结构工程湖北省重点实验室1) 武汉 430070)(中国水利水电第四工程局有限公司2) 西宁 810007) (中国电力建设股份有限公司3) 北京 100048)
0 引 言
边坡失稳是常见的地质灾害之一.边坡稳定性控制的重要手段是变形监测与反馈分析,稳定性趋势预测是其中的技术关键.
大型水电建设及矿山开采形成的大量人工边坡,其稳定状态往往伴随开挖过程而逐渐劣化,变形破坏是与时间相关的演化过程,具有时间效应;另一方面,岩质边坡的破坏往往由局部块体的失稳开始,引起相邻部位失衡,形成连锁扩散效应而整体崩溃,块体的失稳在空间上存在先后关系,在位移监测上表现为空间效应.时间效应体现的单个测点当前位移增长与历史增长规律的差异,而空间效应体现的是边坡变形与整体变形的差异,这两种效应都可以用作边坡稳定性趋势预测.
基于时间效应的稳定性趋势预测模型多借鉴自滑坡启动时间的方法和模型.赵静波等[1]提出阶段时间序列灰色预测模型;Jia等[2]基于支持向量机的单变量预测多变量影响下的边坡位移增长;Li等[3]提出的并行组合形态滤波的最小二乘支持向量机非线性预测方法;曹洋兵等[4]提出的动态灰色-进化神经网络模型;Nie等[5]提出的L-M算法的滑坡中长期预测模型;Wu等[6]采用gm(1,1)模型对分形维数的拟合函数进行优化的方法.谈小龙等[7]将边坡变形时间序列分解为趋势项和随机项的变形组合预测模型;郭运华等[8]将位移分解为开挖卸荷项、时变项、年度周期项的趋势叠加预测模型.这些方法的核心是将当前的位移增长规律与历史监测记录进行对比,来判断边坡未来的稳定性趋势,见图1.

图1 边坡稳定性预测的时间趋势方法
部分学者也意识到单一测点时间趋势分析的局限性,在利用多测点信息方面做了一些探索性的工作,李世贵等[9]提出的发挥多测点相互影响作用的多点灰色模型;何习平等[10]建立的加权多点灰色预测模型;秦栋等[11]提出的考虑不同测点之间相互作用的空间自回归模型等.这些方法仍属于考虑了空间效应的时间趋势方法.
文献[12]根据主观概率交叉影响分析预测复杂动态系统发展趋势的原理,发展了一种考虑所有位移测点间位移增长关系的交叉影响空间分析方法,成功应用于大岗山右岸岩质边坡稳定性预测,取得了较好的效果.
为了进一步研究这一方法的内在机制,本文建立不同约束状态的质点对碰撞、多质点复杂碰撞的模型来进一步交叉影响分析的原理,通过构造隐含不同位移趋势的多个位移增长函数来说明该方法的实现过程,并应用到地铁基坑围护桩位移的研究分析.
1 基于质点碰撞原理的交叉影响分析法
1.1 两质点的约束状态与影响关系
考查两个成对质点构成的简易系统,漏壶代表阻尼,连接的弹簧表示弹性位移.由于质点所受的约束不同,两个成对质点在受到扰动而相互影响时,共有三种偏离原位置的状态.第一种是两个质点A,B均有限偏离原位置,见图2a);第二种是有约束块体C受扰动而影响到无约束质点D,D的偏离远大于C,见图2b);第三种是无约束质点受扰动影响有约束质点后,约束质点反作用到无约束质点,见图2c)~d),其中c)代表较弱的扰动而d)代表强扰动下的反作用.

图2 简易质点对的约束关系与影响结果
各质点偏离原位置的特征,可以用两质点偏离距离的比值为:P(B/A)=b/a,P(D/C)=d/c,P(F/E)=f/e,P(H/G)=h/g,显然有P(H/G)<0 对于有多个质点的复杂系统,两个质点之间的影响关系还可以通过第三个质点传递而建立联系,见图3.质点A对B的影响还可以通过质点C,D,E产生间接影响(暂时不计入C,D,E之间的相互影响).表1为系统内各子系统间的相互影响关系.表1中质点A除了与B直接产生影响P(B/A)外,还通过质点E与B产生间接影响,则A对B影响的总和可记为T(B/A)=P(A/A)×P(B/A)+P(E/A)P(B/E)+P(B/A)P(B/B),即 T(B/A)=2P(B/A)+P(E/A)P(B/E) (1) T(B/A)为A对B影响的总和,推广到质点个数为N+2的复杂系统,将系统中所有间接影响计入,则A对B的总和影响因子为 T(B/A)=2P(B/A)+∑P(i/A)P(B/i) (2) 式中:i为A,B之外的任意第三个质点. 图3 多质点间的影响关系 式(2)的计算,可以通过矩阵运算来实现. 表1 多质点直接影响因子表 表1中行表头与列表头部分均为质点名称,第i行第j列元素代表质点i对质点j的影响.影响因子表构成一个矩阵M,则质点i对质点j的总和影响因子正好是M2的相应元素.这一关系也可以表示成总和影响因子表,见表2. 表2 总和影响因子表 总和影响因子的求解过程可以看出,与影响矩阵M相比,M2挖掘了两质点间接的影响关系.实际上,表2中总和影响因子还未计入作为影响传递中介的多个第三质点间的影响,图2中的A通过C,D,E对B产生影响时,未考虑C,D,E相互间的影响.要考虑传递介质间的相互影响,还需要对M2进一步求平方,得到各质点间交叉影响因子表,元素计算为 T(Ai,Aj)=2T(Aj/Ai)+ ∑T(Ak/Ai)T(Aj/Ak) (3) 式中:Ak为Ai,Aj外的任意元素.由于T(Ak/Ai)由式(2)求得,式(2)中的∑P(i/Ai)P(Ak/i)包含了所有影响传递中介i对Ak的影响,式(3)中∑T(Ak/Ai)T(Aj/Ak)项中,Ak又成了影响传递中介,这两次求和过程计入了各影响中介之间的交叉影响关系,见图4. 图4 交叉影响的耦合效应 由图4可知,若质点B约束不足,则必然A、C对B的影响均偏大,当求解M2时,A对B的总和影响中,A,C的作用也被计入而强化;当求解M4时,A对B的交叉影响中,除了A,C的作用因被再次计入而强化,A与C之间的影响关系也被计入,形成交叉影响效应. 边坡位移的空间分析就是要找出那些可能最先失稳的局部块体,也就是上述模型中的欠约束质点.在获得稳定边坡各块体间的相互影响关系矩阵M后,假定边坡系统发生解体,构成系统的各部分块体间不断调整位置直到新的平衡或者崩溃,那么交叉影响矩阵M2就是各块体偏离原位置的最终状态预测. 实际工程中,边坡各块体间的影响关系,可以通过不同位置开挖卸荷引起的位移增量来映射,且实测值可认为是直接影响与间接影响的和,将多个时段位移增量关系,列于表2中.前面理论模型中的影响关系采用的是位移增长比例关系,即将每行除于该行表头元素的实测增量,形成影响因子表.但当该行表头元素实测增量接近于零时,除操作将造成该行元素严重放大而失效,因此,一般不进行除操作,直接采用实测的对应位移增量作为各测点间影响的关系映射,不影响分析结果. 对表2构成的矩阵进行乘方操作,获得表3交叉影响分析表.对交叉影响因子表各行求和,称为影响度,代表对应块体扰动对所有块体的影响之和;各列之和称为依存度,代表对应块体受到其他部位影响后的响应之和.各列交叉影响因子与影响度列的相关系数,称为协调度. 表3 交叉影响分析表 对依存度从大到小排序就是测点部位失稳可能性的大小顺序. 若只有部分影响信息被监测到,比如,个别设备安装滞后情形,会导致影响因子部分缺失的情形,典型的为上三角部分元素缺失,见表4. 表4 信息缺失情形下的总和影响因子表 由表4可知,由于P(D/B)缺失,求解交叉影响因子T(B,D)时:T(B,D)=P(A/B)×P(D/A)+1×P(D/B)+P(C/B)×P(D/C)+P(D/B)×1+P(E/B)×P(D/E),由于P(D/B),P(E/B),P(D/A),P(D/B)缺失,则剩余项T(D/B)=P(C/B)×P(D/C)仍然可以获得一部分状态信息. 因此,通过交叉影响因子矩阵乘仍可以最大限度地挖掘系统状态信息.但需要尽量避免选择的时间段缺失信息过多.当需要对新安装设备区域的约束状态进行评估时,影响因子应采用最新数据,避免影响因子表中信息缺失过多. 根据大岗山水电站岩质高边坡位移增长实测规律,施工期的位移增长主要影响因素是开挖卸荷作用,带有明显的与开挖过程相对应的阶段性突变特点,其次与岩体蠕变及年度温度波动相关(见图5),总位移的增长模型,可以表示成三项叠加的形式. S(t)=a1(1-a2e-a2x)a4+a5(1-a6e-a7t)a8+ (4) 式中:a1~a10均为参数,在边坡不同位置其值可能各不相同.等式右侧第一项为开挖卸荷引起的位移,x为开挖面到监测点的距离;第二项为时变位移;第三项为年度温度波动的影响. 图5 典型人工边坡位移增长规律 根据实测数据统计分析,开挖卸荷引起的位移占主导,占比一般60%~80%,年度温度波动引起的位移波动量0.2~0.5 mm,蠕变引起的位移3~10 mm,视岩性及边坡形态而异. 依据实测位移增长函数特征,构造类似函数簇,用于验证交叉影响分析,见图6,模拟函数a)采用温度波动影响函数b),随机函数c),位移增长函数d)叠加而成,一共八个不同的函数,位移增长函数d)包括了开挖卸荷的影响及时变影响. 图6 含噪声模拟位移增长曲线 若按常规时间趋势分析方法,图6a)中的位移增长,在250步以后,与前期的大幅增长相比,具有明显的收敛趋势特征,位移增速大幅降低,易误判为边坡已趋于稳定.当然这里因为函数构造方法的原因,可能是温度波动的影响,下面采用交叉影响分析方法来进行分析. 利用图6a)中的数据,采用交叉影响分析,获得的交叉影响分析表,见表5. 表5 交叉影响分析表 表中第一列表示计算位移增量的开始步,第二列是结束步,中间8列均为函数对应的位移增量,表5为矩阵乘方后的结果. 从第一、二列的增量步数的安排,可以发现,增量覆盖了从178步到280步的所有阶段,且还存在部分重叠.各列增量的比较,实际上是对位移增长曲线上多个阶段的对比,协调度是该列与影响度列的相关关系,代表了单个测点增长与整体增长的协调性;依存度为该测点的总增量,代表了偏离原位置可能性的大小. 将依存度及协调度见图7. 图7 异常趋势识别结果 由图7可知,依存度排序为8>5>7>6,说明边坡中可能最先失稳的块体依次为8,5,7,6依次类推.对照图6d)中的8,5,7的位移仍在快速增长,并非如时间趋势分析的趋于收敛的结论.函数2的协调度与其他不同,原因是自178步开始至280步,函数2在这一段期间已停止增长,与其他函数继续增长的规律不一致. 从上述分析可知,对所有测点具有共性的干扰因素,并不会影响排序操作,因此,交叉影响分析可以在一定程度上过滤环境因素(如周期性温度波动)、噪声(如爆破、地震)对监测结果的影响,识别被掩盖的变形趋势. 武汉地铁光谷五路站位于武汉市东湖新技术开发区光谷五路与神墩一路交汇处,车站主体基坑长241.33 m、宽56 m、深度26 m,中部基槽深达32 m.车站主体围护结构采用Ф1 200@1 800 mm钻孔灌注桩加内支撑方案.冠梁采用尺寸为1 200 mm×1 000 mm钢筋混凝土结构,冠梁高程37 m,顶部采用1∶1放坡形式过渡至自然地表高程,三道钢筋混凝土内支撑尺寸为1 000 mm×800 mm,设置高程分别为37,28,21.5 m.采用明挖顺做法施工,即先施工围护结构的钻孔灌注桩,待钻孔桩达到设计强度后,再进行基坑开挖、支撑、回筑施工. 各岩土层依次为素填土,层厚0~1 m;黏土,层厚2~10.5 m;强风化泥岩,层厚0.3~5.8 m;中风化泥岩,最大层厚45.4 m. 开挖作业自2015年12月10日开始第一层开挖,20日开始第二层支撑浇筑,25日开始第二层开挖.2016年3月下旬全部开挖完成.由于基坑布置为长方形,周边无邻近建筑物,可以视为对称基坑,取其1/4研究其开挖期间围护桩顶水平位移,布置图见图8,实测过程曲线见图9. 图8 基坑监测仪器布置示意图 TP为围护桩顶位移监测点,沿基坑北侧共依次设置TP2~TP18共16个测点,其中TP16缺失,图8中标出七个.以基坑北侧桩顶水平位移为分析对象. 图9 实测围护桩顶水平位移过程曲线 由于受温度变化及施工过程影响,实测曲线难于根据时间分析方法预测基坑稳定状态.对TP2~TP18进行长期交叉影响分析,见图10. 图10 围护桩顶水平位移交叉影响分析结果 根据前面研究结果,图10中依存度排序第一的测点为TP18,依存度绝对值超出其他测点3倍,为变形异常区域,现场查勘分析原因为邻近集水井渗漏影响桩周土体缘故. 文中基于多质点的碰撞机制建立了岩土工程位移信息的交叉影响空间分析理论,通过构造含周期性影响因子及噪声的模拟函数,验证交叉影响分析的识别能力.结果表明,交叉影响分析可以根据当前的多测点位移增量关系预测监测对象内与整体变形趋势不一致的局部测点,可用于监测成果的空间分析与趋势预测.研究还发现,交叉影响分析具有一定的抗干扰能力,可以有效过滤对所有测点具有共性的干扰因素,挖掘被掩盖的变形趋势.1.2 多质点系统内部的影响关系
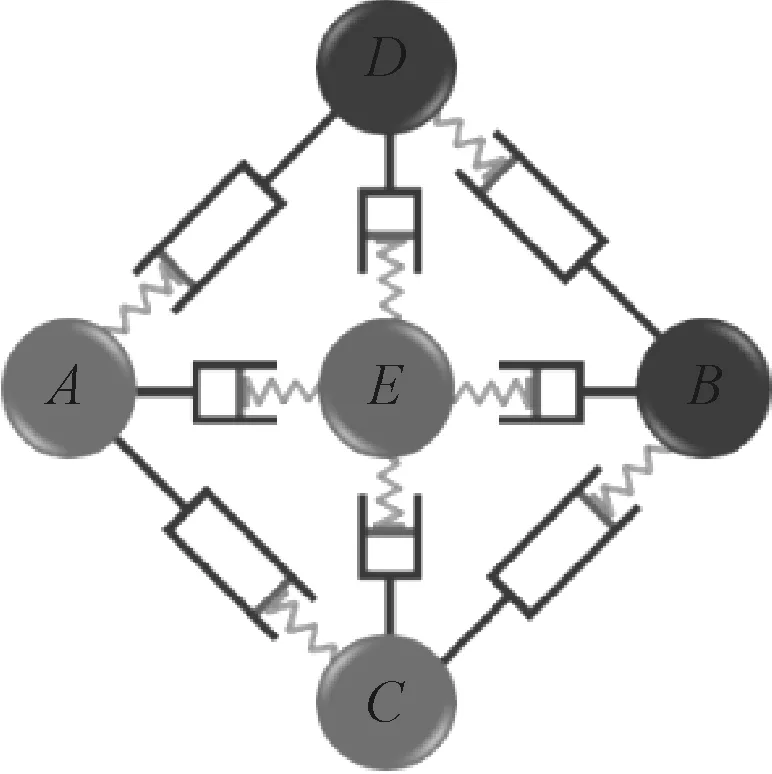



1.3 交叉影响趋势预测的内涵

1.4 部分信息缺失条件下的交叉影响矩阵

2 噪声掩盖下的异常趋势识别
2.1 人工边坡位移增长特点

2.2 含噪声位移增长模拟函数构造

2.3 欠约束块体测点的识别


3 工程应用



4 结束语
——以徐州高层小区为例

