聚烯烃弹性体相对分子质量与特性黏数及熔体流动速率的关系

金 钊，韩书亮，李昊坤，张晓萌，宋文波

（中国石化 北京化工研究院，北京 100013）

聚烯烃弹性体（POE）是指乙烯与丙烯、1-丁烯、1-己烯、1-辛烯等α-烯烃共聚得到的一类高性能聚烯烃材料［1-2］。由于具有优良的耐老化性、耐腐蚀性和耐热性等，POE 广泛应用于汽车、建材、电线电缆等领域［3-6］，但国内至今还未能实现POE的工业化生产［7］。相对分子质量及其分布是影响POE 性能的重要因素之一，在生产和应用中，POE的相对分子质量可以体现为熔体流动速率（MFR），不同MFR 的POE 加工方法差异很大。此外，也可以使用特性黏数（［η］）表征POE 的相对分子质量。对传统聚烯烃材料（如聚乙烯（PE），聚丙烯（PP）等）的Mw与［η］，MFR 关系的研究已较为完备［8-11］，一般通过Mark-Houwink 公式和分子流变学理论建立三者关系［12］。国内关于此方面的研究多集中于POE 共混改性领域。Prut 等［13］研究了新型PP 共混POE 材料的相对分子质量对POE 的流变性能的影响，以及共混物的Mw和结晶度与加工性能的关系。Chen 等［14］研究高强度超声波诱导POE 熔融过程中［η］的变化时发现，［η］随辐照时间延长显著降低，同时研究了聚合物熔体的黏弹特性。但目前尚无建立POE 的Mw，［η］，MFR 三者之间定量关系模型的报道。本工作利用Mark-Houwink 公式和修正的泊肃叶定律，构建了Mw，［η］，MFR 三者之间的定量关系模型，以期为POE 的实际生产和应用提供参考。

1 实验部分

1.1 原料

三种不同共聚单体的POE，分别为乙烯/1-辛烯（E-O）共聚物，乙烯/1-己烯（E-H）共聚物，乙烯/1-丁烯（E-B）共聚物，均为中国石化北京化工研究院生产。

1.2 测试方法及仪器

相对分子质量及其分布采用Polymer Laboratories公司PL-GPC 220 型高温凝胶色谱仪测试：色谱柱为3 根串联的Plgel 10 μm MIXED-B 柱，溶剂及流动相均为1，2，4-三氯苯（含0.025%（w）抗氧剂2，6-二丁基对甲酚），柱温150 ℃，流量1.0 mL/min，采用窄分布聚苯乙烯标样进行普适标定。MFR 采用Ceast 公司CEAST6942 型熔体流动速率仪，按GB/T 3682.2—2018［15］规定的方法测定：190 ℃，2.16 kg。［η］采用马尔文公司VISCOTEK model 430 型黏度仪测试：溶剂为十氢萘，溶解温度150 ℃，溶解1 h，POE 溶液的质量浓度为1 g/L，测试时每个试样测4 次以上，对有效数据取平均值确保准确性。

2 结果与讨论

2.1 POE 试样的性质

所选取的POE 试样的性质见表1。

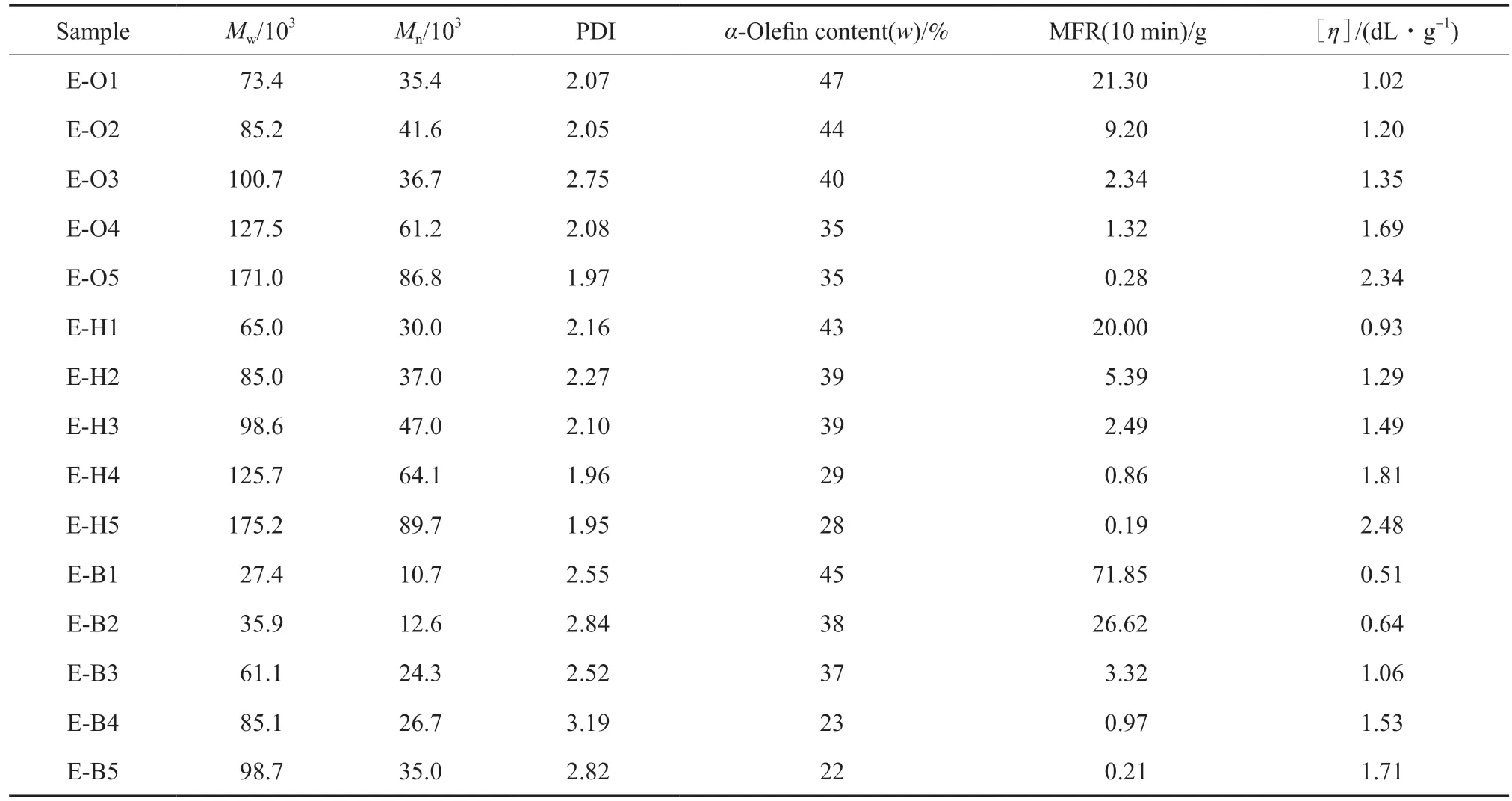
表1 POE 试样的性质Table 1 Characterization of the polyolefin elastomer samples

从表1可知，试样的Mw在2.7×104～1.75×105之间，多分散系数（PDI）在2 ～3 之间，各试样之间差距较小；MFR（10 min）在0.19 ～71.85 g之间。每组试样中，相对分子质量和MFR 从低到高均有分布，而PDI 较为均一，因此具有代表性。

2.2 Mw 与［η］的关系

从表1 可看出，随试样Mw的增大，MFR 逐渐减小，［η］逐渐增大。可通过［η］定量计算Mw，聚合物的Mw与［η］的关系一般遵循Mark-Houwink公式［16］，见式（1）。［η］=KMwα（1）

式中，α 为Mark-Houwink 指数，根据聚合物溶液中溶剂的性质，α 为0.50 ～1；K 为常数。

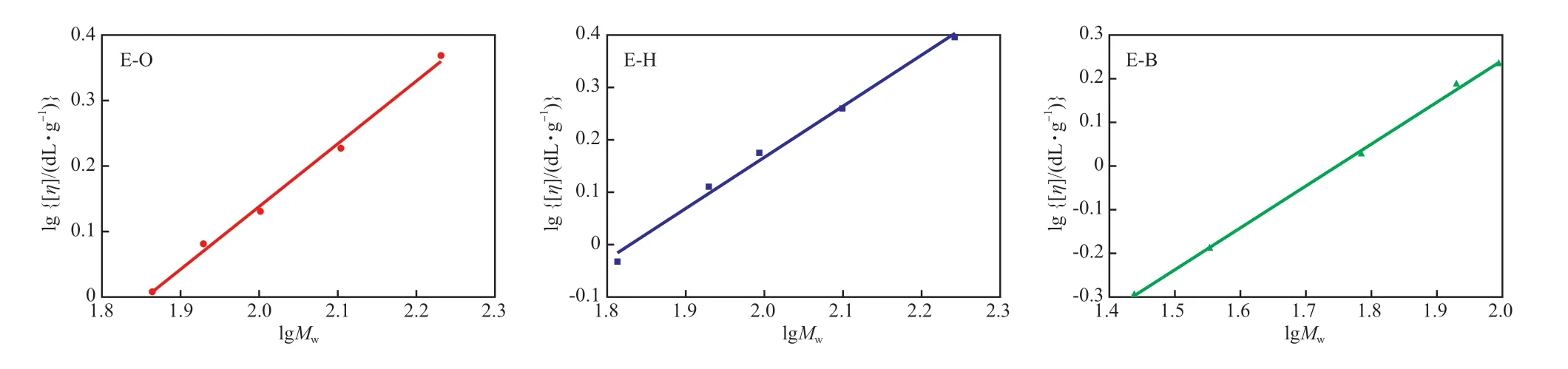
图1 ［η］～Mw 的关系Fig.1 Plots of［η］-Mw.

实际数据处理中，常使用对数形式，即式（2）。

lg［η］=lgK+αlgMw（2）

对lg［η］～lgMw作图并进行线性拟合，截距为lgK，斜率为α。共聚单体不同可能会导致参数不同，故分组作图，然后进行线性拟合，结果见图1。

由图1 和拟合结果可知三组POE 试样的lg［η］～lgMw线性关系明显，拟合相关系数R2均大于0.99。通过计算得到共聚单体为辛烯，己烯，丁烯时α 分别为0.960，0.973，0.961，故根据Mark-Houwink公式，通过测量试样的［η］，可得到估算Mw的计算式，见式（3）～（5）：

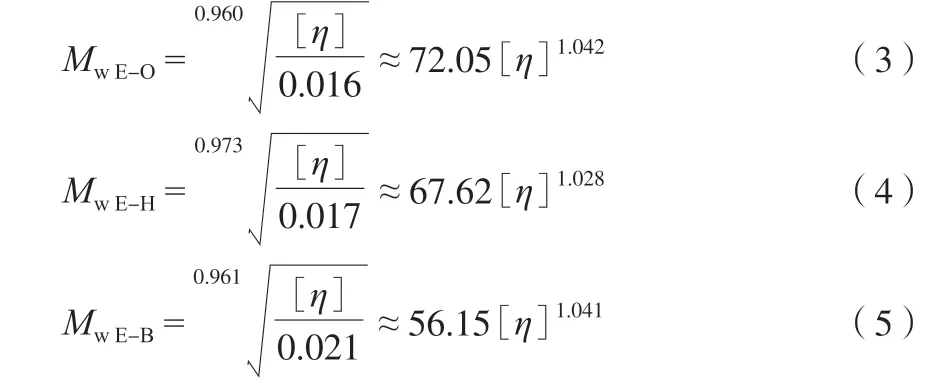
2.3 Mw 与MFR 的关系

在POE 的实际生产和应用中，MFR 是常见的产品参数，且相对容易测得，因此建立POE 的MFR ～Mw之间的定量关系模型非常重要。通常由泊肃叶定律导出MFR 与Mw的关系（见式（6））。

MFR=600ρπR4Δp/8η0L （6）

式中，ρ 为聚合物密度，g/cm3；R 为管道直径，cm；Δp 为压差，Pa；η0为聚合物熔体的零剪切黏度，Pa·s；L 为管道长度，cm。

但在实际应用中，上述公式仅对低剪切速率下的牛顿流体成立，因此还需根据具体情况进一步修正。由分子流变学理论可知，聚合物的η0与Mw存在关系式（7）。

η0=（7）

式中，k 为常数；x 为指数。

结合式（6）～（7）可得式（8）：

式中，k'为常数。

综上可知，MFR 与Mw存在指数关系，取对

数得式（9）：

lgMFR = lgk'-xlgMw（9）

分组对lgMFR ～lgMw作图并进行线性拟合，

截距为lgk'，斜率为-x，结果见图2。

由图2 和拟合结果可知三组POE 试样的lgMFR ～lgMw线性关系也很明显，即式（8）的指数关系对于MFR 与Mw成立。故根据式（8），通过测量POE 试样的MFR，可得到估算Mw的计算式，分别见式（10）～（12）：

2.4 ［η］与MFR 的关系

由式（1）和（8）联立可得式（13）。

根据式（13），可得到三种POE 试样的MFR与［η］的关系，见式（14）～（16）。

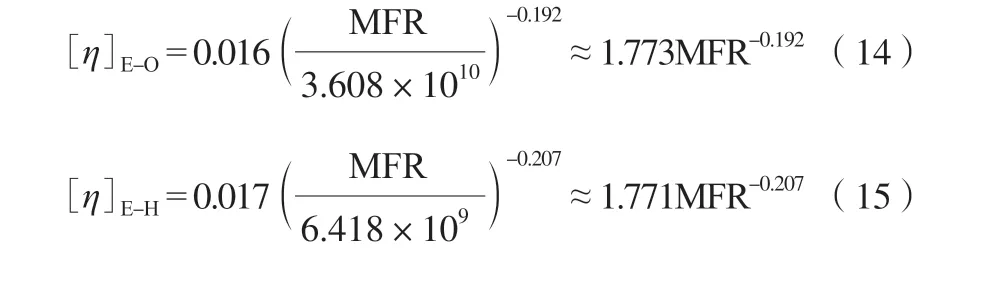
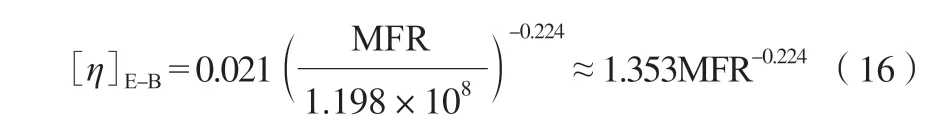
利用上述公式，可通过测量试样的MFR，估算［η］。

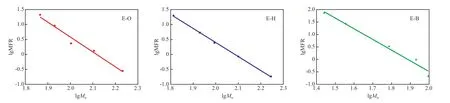
图2 MFR ～Mw 的关系Fig.2 Plots of MFR-Mw.

3 结论

1）选取了辛烯含量35%～47%（w）的E-O共聚物，己烯含量28%～43%（w）的E-H 共聚物，丁烯含量22%～45%（w）的E-B 共聚物进行研究。

2）利用Mark-Houwink 公式可得到由［η］计算Mw的公式：MwE-O=72.05［η］1.042，MwE-H=67.62［η］1.028，MwE-B=56.15［η］1.041。

3）利用泊肃叶定律，通过修正可得到由MFR计算Mw的公式：MwE-O=130.89MFR-0.201，MwE-H=121.69MFR-0.213，MwE-B=76.91MFR-0.233。

4）利用上述公式可得到由MFR 计算［η］的公式：［η］E-O=1.773MFR-0.192，［η］E-H=1.771MFR-0.207，［η］E-B=1.353MFR-0.224。