大型薄壁缠绕型复材壳体的振动特性研究 ①

赵雪尧，任全彬，罗志清，韩 飞,2

(1.中国航天科技集团有限公司四院四十一所 固体火箭发动机燃烧、热结构与内流场国防科技重点实验室，西安 710025；2.西安交通大学，西安 710049)

0 引言

复合材料具有比强度、比模量高，抗疲劳性能好等优良性能，在航空航天领域应用广泛，其中以缠绕型复合材料结构在大型固体火箭轻量化设计中的应用效果最为显著，使固体火箭发动机推重比、火箭射程等关键性能得到大幅提升。

在运输、发射、飞行过程中，固体火箭舱段壳体将承受不同程度的振动载荷，与各向同性的金属壳体相比，复材壳体结构振动特性的研究更为复杂。朱春艳等[1]针对全透波段非金属夹层结构的新一代运载火箭卫星整流罩，建立了由简化的梁、壳等单元构成有限元模型，计算了半罩在不同边界条件下的模态特性。田旭军等[2]为研究泡沫夹芯复合材料加筋结构在工程应用中的振声效果，针对泡沫夹芯复合材料加筋板格结构和钢制板格结构，开展了空气中的振动模态对比试验。刘建良等[3]以玻璃钢板为设计基准，针对碳/玻混杂、橡胶格栅夹层、浮力材料格栅夹层等3种典型复合材料板方案，开展了固有频率和振动加速度振级特性的仿真分析和模型试验研究。黄政等[4]在ANSYS Workbench平台中，采用ACP模块对复合材料螺旋桨的建模进行了分析，介绍了复合材料螺旋桨的建模流程、流体计算模型和固体计算模型。尤军峰[5]根据固体火箭发动机复合材料壳体逐层缠绕的实际工艺进行复合材料壳体细观力学有限元计算方法研究，将计算模型简化为1/60，较真实地建立固体火箭发动机复合材料壳体有限元分析模型，并模拟水压试验工况进行了有限元仿真计算。为复杂构型缠绕性复材壳体的力学仿真提供了重要参考。

本文基于复合材料层合板理论，建立某型固体火箭整流罩壳体的细观动力学分析模型，开展随机振动仿真及关键参数影响规律研究，以期为大型薄壁缠绕型复材壳体结构振动特性研究提供参考。

1 试验原则和方法

1.1 细观分析模型

细观分析方法是将层合板(壳)拆分成多层材料，通过单层材料对复合材料整体进行应力、应变和失效分析的方法。与宏观方法相比，细观方法能对每层及层间的应力、应变和失效方式进行分析；且较于微观分析方法，又极大地减少了节点和单元的数量。因此，细观分析方法是目前使用较为普遍的数值计算方法[6]。

单层材料的结构如图1所示。

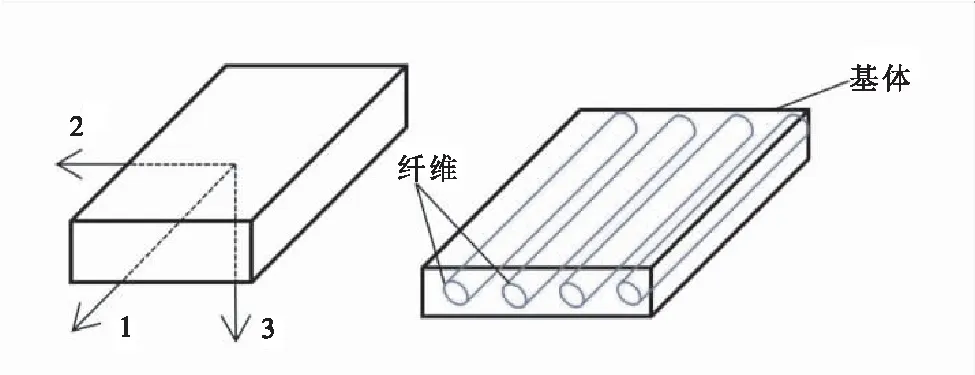
图1 单层纤维示意图

根据单层材料中纤维与基体的配比，可得：

(1)纤维质量分数ψfib

(1)

式中Gfib为纤维质量；Gtot为单层材料总质量；ρfib、ρmat分别为纤维密度和基体密度；Afib、Amat分别为纤维和基体的截面积。

(2)纤维体积分数φfib

(2)

式中Vfib为纤维体积；Vtot为单层材料总体积。

(3)基体质量分数ψmat

(3)

(4)纤维体积分数与基体质量分数的转换

(4)

单层材料可看作是正交各向异性材料，其3个方向的弹性模量、剪切模量和泊松比可由E1、E2、E3、G12、G13、G23、υ12、υ13、υ23表示。这9个参数可由混合法则计算出，最常见的是Jones法则：

E1=φfib·EF1+(1-φfib)·EM

(5)

(6)

E3=E2

(7)

(8)

G13=G12

(9)

G23=φfib·GF23+(1-φfib)·GM

(10)

υ12=φfib·υF12+(1-φfib)·υM

(11)

υ13=υ12

(12)

υ23=φfib·υF23+(1-φfib)·υM

(13)

1.2 层合板等效理论

层合板是由多个单层板粘结而成的，但由于各单层板很薄，层合板的总厚度与其他尺寸相比仍然小得多，在整体上可把层合板视作一块非均质的各向异性薄板。

图2 层合板铺层示意图

各单层板的力学性能和厚度以及其铺层方向和序列决定了整个层合版的性能。由于层合板相当于一块非均质的各向异性薄板，与均质材料结构不同，故须立足于每一单层对层合版进行分析，其基本假设为[7]：

(1)层间变形一致假设；

(2)直法线不变假设；

(3)在厚度方向上的正应力σz=0假设；

(4)单层平面应力状态假设。

基于直法线不变假设，层合板的变形分析可简化为对中面的变性分析。由于层合版沿厚度方向上具有非均质性，在铺层间应力不一定连续，但在每一单层中，沿厚度方向的应力变化是连续函数，故可近似为先分层积分再求和的形式：

(14)

(15)

式中 {N}为层合板所受合力；{M}为层合板所受合力矩；zk为各层坐标。

层合板的合力及合力矩可用矩阵表示：

(16)

式中ε0为层合板的中面应变矩阵；k为曲率矩阵；A为拉伸刚度矩阵；B为耦合刚度矩阵；D为弯曲刚度矩阵。

式(16)即为用应变表示内力的一般层合板的物理方程。对层合板的物理方程进行矩阵运算即可得到层合板的应变矩阵。

2 数值仿真

某型固体火箭整流罩结构外型面为哈克曲线，基本壁厚5 mm，曲线方程为

缠绕纤维的材料参数由1.1节中方法得到，如表1所示。

表1 碳纤维的材料参数

模型中设定单层纤维的厚度为0.25 mm，纤维铺层的方向与层数为[0/90/45/-45/0]4，总厚度为5 mm，模型的铺层设计如图3所示。

有限元的网格划分情况如图4所示。

在壳体尾端截面施加固支边界条件，其模态计算结果如表2与图5所示。为便于对比分析，特将正交方向的2个模态合并。

鉴于结构低频振动特性对于整流罩壳体性能的影响更为显著，对GJB 150.16A-2009《军用装备实验室环境试验方法 第16部分 振动试验》中给出的随机振动条件进行裁剪，随机振动计算输入条件如图6所示。

图3 模型的铺层设计

图4 模型的网格划分

表2 总厚度不同的铺层方式的模态频率

图5 整流罩模型前六阶模态图

图6 随机振动输入的功率谱密度

整流罩壳体的最大应力云图、最大应变云图和位移响应云图如图7所示。可见，在给定的边界条件和输入条件作用下，整流罩壳体头部的振动位移最大，尾端应力最大，而最大应变则处在整流罩壳体的中后部。

图7 随机振动结果云图

3 规律分析

3.1 壳体厚度的影响

重量指标是固体火箭整流罩的关键参数，仿真过程中通过改变层的方式[0/90/45/-45/0]3(总厚3.75 mm)、[0/90/45/-45/0]4(总厚5.00 mm)、[0/90/45/-45/0]5(总厚6.25 mm)，以改变整流罩壳体基本壁厚，模态仿真结果见图8。

由图8可看出，随着壳体厚度增加，在分析频段内，除一阶弯曲振动模态频率未发生显著改变外，整流罩壳体呼吸模态频率均得到明显提升。进一步提取总厚度不同的算例其各相同振型下的模态频率，如表2所示。能明显发现，随着模态阶数的升高，在同一振型情况下，厚度对材料结构的性能影响愈来愈大。

在第2节所示横向随机振动输入条件下3个算例的最大位移功率谱密度曲线对比，如图9所示。

可发现，在给定的振动输入条件下，不同厚度算例对应的整流罩壳体振动位移曲线基本一致。这是由于对于给定的振动输入条件，壳体一阶弯曲振动模态的影响最为显著，而壳体厚度的增加对于一弯模态的影响较小，导致位移功率谱密度曲线未呈现明显差异。实际结构中，整流罩与下面级发动机的连接方式通常为多点连接，在这中连接形式下，整流罩壳体的呼吸模态对于其振动特性的影响将不容忽视。

图8 总厚度不同算例的模态频率对比

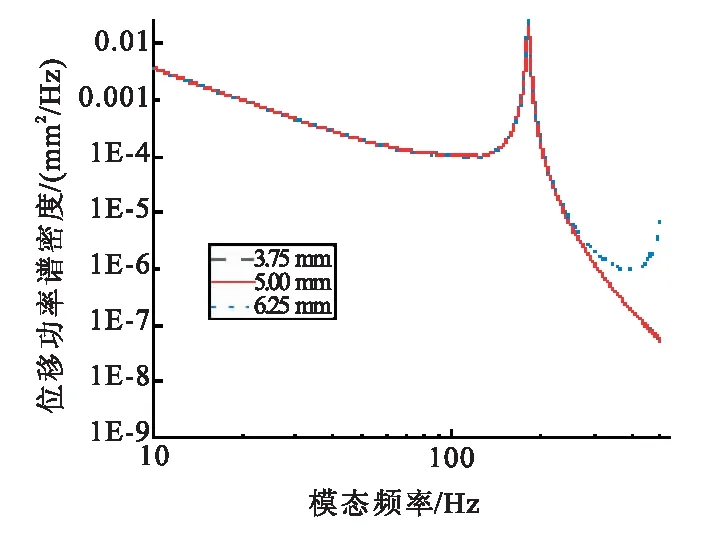
图9 总厚度不同算例的位移功率谱密度对比

图10给出了整流罩壳体底部8点固支边界条件下的随机振动仿真结果。结果表明，随着壳体厚度的增加，壳体的低频振动响应曲线整体向高频偏移，厚度增加33%，模态向高频偏移4%。

3.2 铺层方式的影响

在整流罩厚度5 mm以及单层厚度0.25 mm保持不变的情况下，选择图11中的4种铺层方式算例，分别进行仿真模态计算。

根据计算结果可看出，在[0/90/45/-45/0]4铺层方式下，即当0°、45°和90°铺层同时存在的情况下，其模态频率相对较高。不同铺层方式对应的结构振动响应曲线见图12。

由图12可以看出，采用[0/90/45/-45/0]4铺层方式时，受到整流罩壳体模态频率的提高，结构的低频振动水平显著降低。在保证整流罩壳体厚度不变的情况下，通过优化铺层方式，能够显著改善结构的低频振动特性。

图10 底部8点固支边界条件下的随机振动仿真结果

图11 不同铺层方式算例的模态频率对比

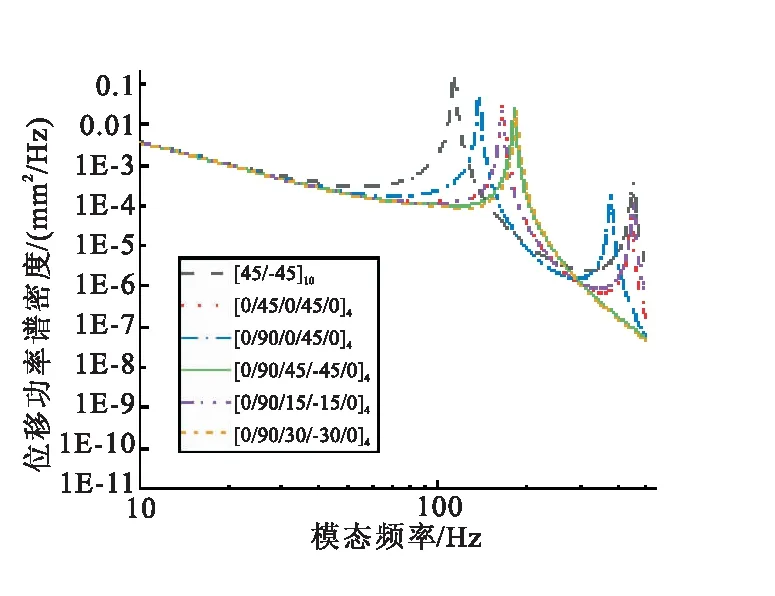
图12 不同铺层方式算例的随机振动响应对比

4 结论

(1)壳体厚度对整流罩壳体呼吸模态的影响较大，在工程中常用的随机振动输入条件作用下，厚度变化对结构振动响应的影响较小。

(2)铺层方式对整流罩壳体的振动特性影响显著，通过优化铺层方式来提高整流罩壳体刚性是更为有效的措施。