多裂缝“应力阴影”的有限元数值模拟

汪道兵，秦 浩，马海燕，李敬法，孙东亮，宇 波*

(1.北京石油化工学院机械工程学院，深水油气管线关键技术与装备北京市重点实验室，北京 102617； 2.中国寰球工程有限公司北京分公司，北京 100012)

近年来，斯伦贝谢公司已开发出一套非常规压裂模型(UFM)用来模拟含天然裂缝性储层的复杂缝网的形成与延伸[1]。多条水力裂缝分支缝同时延伸且相互交叉作用。每一条张开的裂缝对周围岩石及邻近裂缝施加了附加应力，一般定义这种效应为“应力阴影”效应[1-6]。Wu等[1]使用二维位移不连续法(DDM)模拟地应力场，研究了地应力各向异性对水力裂缝间的相互干扰规律，“应力阴影”对缝宽、缝网的几何形态和支撑剂铺置影响明显。Cipolla等[2]利用UFM模拟器研究了Barnett页岩水平井分段压裂施工时裂缝网络形成，并结合微地震监测结果，发现当应力各向异性小，由于“应力阴影”效应的存在，人工裂缝的云点分布较分散。Ripudaman等[3]通过数值模拟发现，当形成复杂裂缝网络时，“应力阴影”对缝宽具有很强的影响，从而影响各段射孔簇的流量分布、整个裂缝网络形态和支撑剂的铺置。刘立峰、Mohamed和Loyd等通过诱导地应力场解析解模拟了地应力差对“应力阴影”的影响[7-15]，如果地层应力差较小或相等时，压裂裂缝会沿无规则天然裂缝向各个方向延伸，从而形成网状裂缝。同时还可向缝内加入纤维等暂堵转向剂，利用“应力阴影”效应增加缝内净压力，迫使裂缝强制转向，人工诱导缝网形成[10，16-22]。

前人对“应力阴影”的研究多依赖解析解、商业数值模拟器或室内实验等手段，多数定性分析了地应力各向异性、岩石力学参数等因素对“应力阴影”的影响，并未定量给出两裂缝干扰区间内的应力分布状态，因此较难给出裂缝间距等关键参数的最优范围。笔者通过有限元数值离散化方法，以弹性力学和水力压裂理论为基础，自行编制程序，数值模拟了2条平行裂缝干扰时的“应力阴影”分布状态，研究了裂缝间距、孔隙压力、两裂缝内压力变化等关键工程参数对“应力阴影”的影响，定量优化了裂缝间距。

1 物理模型

当水力压裂产生2条平行裂缝时，两裂缝间应力场干扰，从而形成“应力阴影”区，物理模型如图1所示。具体假设条件如下[23-24]：

(1)无限大、各向同性地层中间存在2条平行的水力压裂裂缝，2条裂缝长度、宽度相同且保持固定不变，半缝长记为L，缝间距离记为d；

(2)地层远场地应力各向异性，即最大、最小水平主应力分别为σH、σh；

(3)压裂液作用在2条裂缝面上的流体压力分别为P1、P2；

(4)等温变化，即不考虑温度变化对地应力的干扰；

(5)由于油藏厚度较大，可将三维问题简化二维平面应变问题；

(6)不考虑流固耦合，即在给定两缝面压力情形下，考虑两缝间的干扰效应；

(7)地层原始孔隙为Pp，地层流体微可压缩，不考虑应力导致的骨架变形对孔压的影响；

(8)远场左、右边界分别记为ΓL、ΓR，上、下边界分别记为ΓT、ΓB，4个边界上作用着远场应力。

2 数学模型

2.1 控制方程

根据岩石力学理论，忽略岩石基质中的体积力，应力平衡方程为[23-24]：

·σ=0

(1)

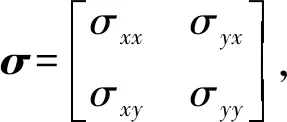
假设岩石为线弹性变形，且为各向异性介质，则应力-应变本构方程为[23-24]：

σeff=D:ε

(2)

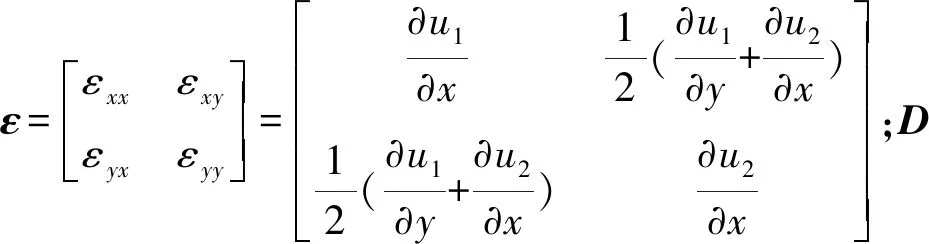
根据有效应力概念，柯西应力张量σ可以分解为[23-24]：

σeff=σ-αppI

(3)

其中：α为Biot弹性常数，α∈[0，1]；pp为地层原始孔隙压力；I为单位张量。

应变张量与位移梯度张量间满足关系式[23-24]：

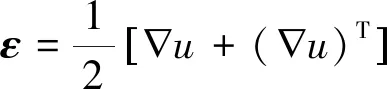
(4)

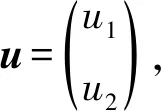
2.2 边界条件

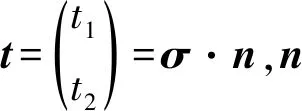
(1)左边界ΓL和右边界ΓR：t1=-σH，u2=0；

(2)上边界ΓT与下边界ΓB：t2=-σh，u1=0；

(3)第1条裂缝：t1=0，t2=P1；

(4)第2条裂缝：t1=0，t2=P2。

2.3 有限元离散化方法

2.3.1 弱形式

根据弹性力学虚功原理，设Ω为图1中的区域，得出控制方程(1)和边界条件组成系统的弱形式为[25]：

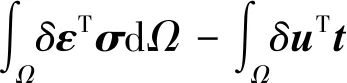
(5)

其中：δu为虚位移向量，δε为虚应变向量。

2.3.2 应力平衡方程的离散化

为了计算结果的稳定性和计算速度，选用线性四边形单元Ωe对求解区域Ω进行有限元离散。根据Galerkin有限元方法，设u=Na(e)，其中N为形函数，a(e)为位移节点，ε=Ba(e)，δu=Nδa(e)，则弱形式(5)离散后变成[25-26]：

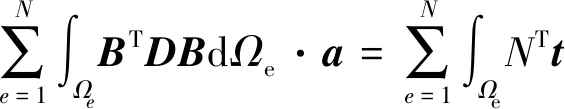
(6)

用Matlab语言编制了有限元程序，为了加快计算速度，刚度矩阵K用稀疏矩阵存储，即K=sparse(allJ， allI， allK)，allI、allJ表示非零元素allK的指标[26]；有限元算法求解出方程(6)后，得出位移节点分布，根据本构关系可以求出应力分量与应变分量，进而分别得出主方向与主应力的大小[23-24]：

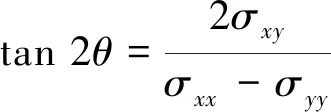
(7)

(8)

其中:θ为主方向；σ1、σ2为两水平主应力大小，且σ1>σ2，进而可以得出区域中的主方向与主应力的平面分布状态。

3 数值模拟结果3.1 裂缝间距

选择两裂缝中心点A(0，0)为坐标原点，建立直角坐标系，物理模型基本输入参数如表1所示，根据式(7)与式(8)，模拟了在不同间距(40、60、80、100、120、140、160、180 m)下，两裂缝中心位置处点A(0，0)、B(-250，0)处的主应力与主方向演化规律，结果如图2所示。图中横坐标x=0表示中心点A，x=-250代表点B，点A、点B具体位置如图1所示。图2中主方向、主应力按式(7)、式(8)计算，其中主应力只计算最大主应力σ1，横、纵坐标为归一化数值，即以间距为180 m下的主应力和主方向值为参考值，计算公式为：归一化主应力=每个间距下主应力/最大间距(d=180 m)下主应力，归一化主方向、归一化间距可依此类推。从图2中可以看出，当裂缝间距达到临界值(0.65左右)时，主应力与主方向值发生突变，此时2条裂缝间应力干扰较强。

表1 基本输入参数

Table 1 Basic input parameters

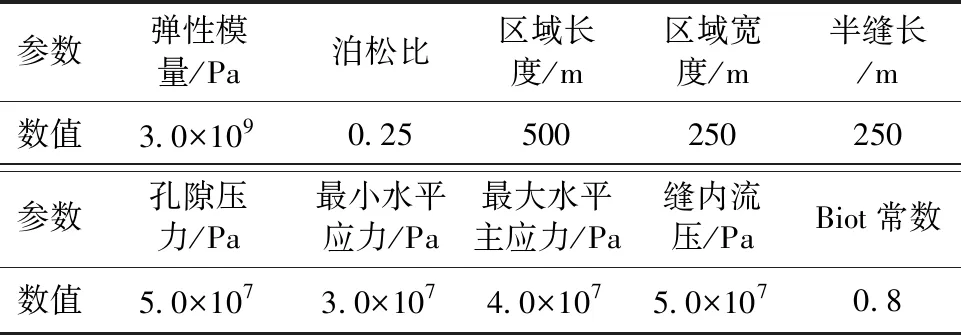
参数弹性模量/Pa泊松比区域长度/m区域宽度/m半缝长/m数值3.0×1090.25500250250参数孔隙压力/Pa最小水平应力/Pa最大水平主应力/Pa缝内流压/PaBiot常数数值5.0×1073.0×1074.0×1075.0×1070.8

为了验证以上规律，改变裂缝内的流压比，分别模拟不同压力比(p2/p1=1.0、1.5和2.0)下的归一化主应力与主方向值随归一化裂缝间距的变化曲线，结果如图3所示。由图3可以看出，仍出现此临界值，变化规律与图2完全相似。图中裂缝临界区间位于区间(0.65， 0.75)内，即对应裂缝(120，140)范围内；当裂缝间距小于或大于此值时，主方向和主应力值变化微小；而达到此值时，主应力值和主方向值变化较强。因此，在本模型情形下，裂缝间距为140 m左右时，缝间应力干扰较强，按此方式布缝，有利于促进水力压裂过程中复杂缝网的形成，对页岩气、致密油气藏等非常规水力压裂设计方案具有指导作用[9-14]。

根据经典水力压裂理论，裂缝内净压力计算式为：

(9)

其中：pnet为裂缝内净压力，MPa；κ为常数，椭圆形缝，其值为16/π；E′为岩石平面模量，E′=E/(1-ν2)，MPa；E为岩石弹性模量，MPa，ν为泊松比；q为液体注入排量，m3/min；xf为裂缝半长，m。

根据式(9)，在给定缝内压力、裂缝尺寸情况下，可以反算出注入排量大小，按表1中参数，裂缝间距为140 m、裂缝半长为250 m、缝高为50 m、缝内流压为50 MPa时，注入排量约为4.8 m3/min。即在此排量下，两裂缝间发生干扰，若排量较低(低于1 m3/min)，缝内压力较小，两缝间不发生干扰。

为进一步分析此情况下其他因素对“应力阴影”效应的影响，分别模拟了两裂缝间距为140 m时的主应力、主方向分布，并对其他参数(孔隙压力、缝面流体压力、两缝面流压比)进行了敏感性分析。

3.2 主应力与主方向分布

按表1中输入参数，模拟了裂缝间距140 m下的主应力、主方向分布平面图，结果如图4、图5所示。从图4、图5中可以看出，两裂缝尖端处主方向变化较大，主应力集中于此处，若继续注入压裂液增加缝内净压力，裂缝尖存在裂缝转向可能性；主应力图上两缝之间存在一深蓝色区域，即此处主值较小，裂缝容易开裂，可利用此区域的“应力阴影”促使两主裂缝沟通，形成复杂缝网[23-24]。

3.3 两缝面流体压力比

按表1中所列参数，固定其他参数不变，模拟不同流压比值下主应力值与主方向的演化规律，结果如图6所示。由图6中可以看出，随着两裂缝间压力比值的增大，主应力值单调增加，主方向单调递减；当流压比值超过2.5～3.0后，主值变化幅度不大，因此可以控制比值在0.5～2.0范围内，增强缝间干扰，促使后续人工裂缝转向，形成复杂缝网；现场可以注入纤维等转向剂，诱使缝间流压变化，增强缝间干扰，提高复杂缝网形成的可能性[9，16-18，20]。根据式(9)可知，缝内净压力与注入排量、压裂液黏度有关，因此现场可采用多级交替变排量施工、多次停泵、使用不同稠化剂浓度的压裂液、改变交联比等来调节排量和液体黏度，实现两缝间压力波动变化；另外配合可降解纤维等暂堵转向剂封堵人工裂缝，再调节排量和液体黏度，诱使裂缝间压力变化，形成复杂缝网。

3.4 孔隙压力

按表1 中所列参数，模拟了不同孔隙压力下主应力与主方向的变化情况，结果如图7所示。由图7中可以看出，随着孔隙压力的增加，主应力线性增大，主方向缓慢减小，说明油田生产一段时间后，地层压力减小，可以诱使主方向发生较大变化，主应力值减小，此时裂缝容易从新方向起裂；而增加孔隙压力效果不明显，孔压从30 MPa增加至70 MPa，主方向仅变化2～3°左右，幅度较小，因此开采降压更为有利于裂缝重新定向[10-15，18]。类似于重复压裂施工，现场压裂施工前，可以使油气井生产一段时间，使地层压力逐步下降到一定水平；或增大工作制度，使油气井压力快速下降，之后再进行压裂施工。

3.5 缝面流体压力

按表1 中所列参数，保持两裂缝中流压相同，改变作用于缝面上流体压力大小，模拟了不同压力下主应力与主方向的变化，结果如图8所示。由图8中可以看出，随着流体压力的增加，主应力线性增大，主方向线性减小，说明可以通过提高压裂液黏度、增大注入液量的办法来增强缝间干扰，促使裂缝重新定向，形成复杂缝网[18-22]。按式(9)，在压裂施工时可以改变液体黏度、增大液量、增加注入时间等工艺措施等达到改变流压目的。

3.6 模型验证

取表1中的最大、最小主应力数值，孔隙压力、井壁压力均为0，采用上述有限元方法模拟半径为0.1 m、井眼1 m处的周向应力大小，周向应力可通过式(10)计算得到，并与弹性力学中的周向应力解析解模拟结果比较[18，23-24]，结果如图9所示。由图9可以看出，二者完全一致，说明有限元数值解可靠。

σθ=σxsin2θ+σycos2θ-σxysin2θ

(10)

4 结论

(1) 根据弹性力学虚功原理，采用有限元算法自行编程模拟了不同裂缝间距下主应力和主方向的平面分布图，结果发现裂缝间距存在一最佳临界值，此时主应力与主方向值发生突变，2条裂缝间应力干扰较强，据此可以优化分段压裂设计时的布缝模式。

(2)模拟了最优裂缝间距的主应力、主方向平面分布状态，两裂缝尖端处主方向变化较大，主应力集中于此处，若继续注入压裂液增加缝内净压力，裂缝尖存在裂缝转向可能性；主应力图上两缝之间存在一深蓝色区域，即此处主值较小，裂缝容易开裂，可利用此区域的“应力阴影”促使两主裂缝沟通，形成复杂缝网。并根据缝内压力反求出注入排量约为4.8 m3/min。即在此排量下，两裂缝间发生干扰，若排量较低(低于1 m3/min)，缝内压力较小，两缝间不发生干扰。

(3) 在最佳间距条件下，分析了不同孔隙压力、缝面流压及流压比值下对两缝间“应力阴影”的影响，压裂实际施工可采用多级交替变排量、多次停泵、使用不同稠化剂浓度的压裂液、改变压裂液交联比等来调节排量和液体黏度，并配合人工转向剂暂堵裂缝等工艺措施，诱使多裂缝间压力变化，控制两缝流压比值在0.5～2.0区间内，增强缝间干扰，促使后续人工裂缝转向，提高复杂缝网形成的可能性。

(4) 在给定布缝方式下，两缝间干扰与流压及缝内流压比密切相关，压裂施工过程中改变液体黏度与排量、增大注液量与注入时间以及注入纤维暂堵转向剂等工艺措施可诱使压裂过程发生缝间干扰，因此细致研究复杂裂缝间压力如何分布对水力压裂形成复杂缝网非常关键。