风电增速箱行星轮系瞬态接触动力学分析

李 进，张洪伟，樊恒明，窦艳涛

(北京石油化工学院机械工程学院，北京 102617)

风电机组特殊的工作环境以及大型化的发展趋势，对传动装置的可靠性以及稳定性提出了更高要求。增速箱作为整个风力发电机中造价较高、维护昂贵的核心组件，是影响机组性能和可靠服役的关键。国际风能大会对风机故障的统计中，齿轮增速器故障占了12%，齿轮箱运行环境恶劣、传输负载易突变、恶劣的服役条件加速了齿轮箱系统的疲劳破坏，尤其是关键零部件齿轮的故障问题尤为突出，直接影响增速箱的使用寿命，所以对增速箱中的行星轮系进行接触动力学分析显得尤为重要。

目前国内外学者都围绕增速箱做了富有成效的研究工作，在国内，霍忠堂等[1]运用非线性有限元软件ANSYS/LS-DYNA对行星齿轮系的接触—冲击动态啮合情况进行分析，得出行星架转速的增加量与齿轮间啮合应力的变化呈非线性关系；陈钟华等[2]进行了风电机组复合行星轮系虚拟样机仿真研究，通过运动学分析和静力学计算验证了虚拟样机仿真模型的正确性；杨海湾等[3]以某一型号的风力发电机增速齿轮箱行星轮系为研究对象，充分考虑齿侧间隙、轴承间隙及齿面摩擦等因素，采用冲击-接触动力学求解，得出转速不同时其啮合应力存在延迟现象，冲击应力随转速增加而增大；薛丹[4]完成了变风载下2.5 MW风电增速器行星轮系动力学特性分析，得出不同啮合刚度组合对行星轮系低阶固有频率影响较小、高阶固有频率影响较大；国外学者Kahraman[5]建立了只考虑扭转的含有复合行星轮系的自由振动特性；Hbaieb等[6]采用纯扭转模型分析了行星轮系的时变刚度对系统固有频率的影响，结果表明，时变刚度的变化会引起参数失稳；Dhouib[7]建立复合行星轮系的振动线性模型，研究了不同行星轮组数、不同类型行星轮之间的相对位置以及陀螺现象对系统固有频率的影响，结果表明，行星轮的增加会改变固有频率的重复性，相对位置对固有频率的影响不大，固有频率对陀螺现象敏感。国内外学者均未证明行星轮系接触应力和弯曲应力对行星轮系强度校核的影响大小[8-9]。

笔者设计了风电用5.5 MW增速箱，针对低速级行星轮系建立了刚柔混合多体有限元模型，进行了瞬态接触动力学计算，对计算得到的接触应力进行了分析，并与理论值进行了比较。

1 5.5 MW增速箱工作原理

设计了5.5 MW的基于功率分流式行星差动结构的增速箱，该齿轮箱结构紧凑，通过功率分流降低齿轮载荷，减小整体尺寸。结构由四级传动构成：第一级与第二级均采用NGW斜齿行星轮系；第三级采用2Z-X型斜齿差动轮系；第四级为平行轴斜齿齿轮。通过对第一级NGW行星轮系采用中心轮浮动，第二级NGW行星轮系采用中心轮和内齿圈浮动，第三级差动轮系采用内齿圈浮动，简化了箱体整体的结构，使得结构紧凑、传动平稳，而且具有良好的均载性能。在传动过程中主要通过第一级、第三级、第四级进行传动比的增加，起到转速的增加，第二级起到配重及功率输入的作用。当外部载荷输入到第一级行星架上，该行星架会同时作用于第一级行星轮和第二级内齿圈上，然后第一级功率经第一级行星轮传递到第一级太阳轮，第二级功率经本级行星轮传递到本级太阳轮上，最后整个功率再由第一级中心轮直接传递到第三级的行星架上，由第二级中心轮传递给第三级内齿圈上，第三级通过将第一、二级的功率经行星轮合成由中心轮输出到第四级进行输出。设计的增速箱的三维图如图1所示。

2 行星轮系瞬态接触分析

2.1 行星轮系模型处理

设计的增速箱在前三级均采用了行星轮系，且第一级为低速级，会承受到较大的载荷和冲击，以此为研究对象，进行接触动力学研究。由于斜齿行星轮系结构比较复杂，在分析中采用UG进行几何建模。

斜齿行星轮系的几何模型如图2(a)所示。太阳轮分度圆直径为730.43 mm，行星轮分度圆直径为1 069.57 mm，内齿圈分度圆直径为2 869.56 mm，将建立好的模型导入到ANSYS Workbench中进行分析。该模型比较复杂，直接分析不仅对计算机要求较高，而且计算量会非常大，耗时耗力。笔者主要是查看行星轮系轮齿动态接触状态，重点是齿与齿之间的接触变化，故对其中的轴承进行省略，对行星架进行了简化。将均匀分布的3个行星轮只保留1个参与计算，简化结果如图2(b)所示。

齿轮材料为20CrMnMo，参数为:弹性模量为200 GPa，泊松比为0.3，密度为7 850 kg/m3。行星轮系参数为：模数为25，太阳轮的齿数为28；行星轮的齿数为41，个数为3；内齿圈齿数为110；螺旋角为16.597 8°。

2.2 刚柔混合建模技术

瞬态啮合对建模中的精确度要求非常严格，很小的误差都会导致接触特性很大的不同，甚至结果不收敛无法计算，所以建模过程中一定要提高建模精度，并且保证齿轮的装配准确无误。

刚柔混合建模是指在分析一个装配体时，有些部件不参与或者影响可以忽略，但是其又不可以被删除时，将其处理成刚性部件，使其不参与运算以减小计算量。通过外部节点与刚性体之间创建运动副实现刚性体与柔性体的连接。对行星轮系的瞬态接触动力学分析不考虑行星架的影响，故可将行星架作为刚性体处理，太阳轮、行星轮、内齿圈作为柔性体。

2.3 网格划分

网格划分是建立有限元模型的重要环节，网格划分的质量对模型有限元分析结果的准确度影响较大[10]。高质量网格不仅可以得到准确的结果，同时还有助于求解的收敛。自由网格划分对于结构形式复杂的零件更容易划分网格；映射方法一般可得到较规则的网格，但如果结构复杂，划分比较困难。由于齿轮较复杂，采用自由网格划分，模型整体网格划分情况见图3，接触区域网格划分情况见图4。该模型节点数为353 413个，网格数为72 264个。

2.4 边界条件及载荷施加

在该行星轮系中，太阳轮、行星架都是绕轴线方向进行自转，内齿圈固定在齿轮箱上，行星轮既有自转又有公转，故施加的运动副有体-地连接副、固定副、体-体连接副。太阳轮与行星架添加的旋转副为体-地连接副，运动副具体添加情况见图5。这里体就是太阳轮、行星轮，太阳轮和行星架只保留绕Z轴的转动自由度；行星架与行星轮的旋转连接通过添加体-体连接副进行连接，将行星轮定义为运动件，只保留绕Z轴的转动自由度。

齿轮箱动力由第一级行星架输入，动力又经过行星轮传递给中心轮，由中心轮输出，故给太阳轮添加转动副用于输入阻力矩。由于行星轮系经过简化仅有一个行星轮，所以添加阻力矩时取扭矩的1/3。行星架通过带动行星轮绕中心轮公转，使行星轮与固定内齿圈和中心轮相啮合，从而将转矩传递给中心轮，而中心轮通过添加阻力矩，从而使力矩平衡，最终完成整个能量传递过程。

2.5 瞬态动力学计算

齿轮啮合过程分析原理依靠接触力学和瞬态动力学。

接触力学是研究两物体相互接触产生的局部应力和应变分布规律的学科。假设：①接触区发生小变形；②接触面呈椭圆形；③相接触的物体可被看作是弹性半空间，接触面上只作用有分布的垂直压力。凡满足以上假设的接触称为赫兹接触。

瞬态动力学分析也称时间历程分析，是监测随时间变化在载荷作用下的结构响应的分析方法。输入数据可以是时间函数的载荷、静载荷、瞬态载荷和简谐载荷的随意组合。输出数据是随时间变化的位移及其他导出量如应力、应变、力等。

瞬态动力分析的运动方程为：

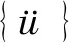
在瞬态动力分析中密度或质点质量、弹性模量及泊松比、阻尼等因素均应考虑，在ANSYS分析过程中密度或质量、弹性模量是必须输入的，忽略阻尼时可以选忽略选项。在瞬态动力学分析中，瞬态分析参数(时间步)的设置比较关键，主要设置的是求解和步长控制的设置。在步长控制中要设置步长结束时间，这里的时间并非真实时间，而是一个相对的时间，但是设置的时间越大，求解的时间就越长，需要的计算机空间就越大，因此设置合理的步长结束时间有助于缩短求解的时间。本次分析中设置的求解时间为0.1 s，最小时间步长为0.002 s，最大时间步长为0.005 s，打开了大变形以保证求解的收敛性。

3 接触应力结果分析

接触应力随时间的变化情况如图6所示。从图6中可以看出，在初始一段时间，接触应力波动较大，而且在第5个时间步出现了最大值，在之后的时间段里波动逐渐减小，最终趋于稳定。在0.1 s时的接触压力云图如图7所示。由图7中可以看到，接触压力发生在齿轮的齿面上，图案呈现椭圆状，在啮合过程中会同时有3个轮齿进行啮合，每个轮齿面上都出现了椭圆形状，而且这些椭圆大小相似。所以，当齿轮齿面发生失效时会以片状进行脱落。经过分析可以得到，此次设计的复合行星轮系的接触应力130 MPa远小于理论计算的许用应力值850 MPa，故该设计满足要求。

应用Von Mises应力对齿轮进行强度校核，故分析时只要查看行星轮与太阳轮啮合过程中的最大应力是否小于许用应力即可判断设计是否合理。0.1 s时的等效应力云图和行星轮等效应力云图分别如图8、图9所示。从图8和图9中可以看到，在轮齿啮合过程中除了齿根处出现应力集中，其他接触部分未出现应力集中现象，而且应力分布分散合理。在图8中可以明显地看到，出现应力集中的3处分别位于3个轮齿的齿根处，而且位置不在同一处，按图8的放置可以将出现最大应力在3个轮齿的上、中、下3个位置，由此可知该设计的应力被很好地分布于不同的轮齿上的不同位置，避免了应力集中在一个轮齿上。从图9中可以看到，在齿根处出现的最大等效应力为214.6 MPa，通过瞬态分析得到的应力值小于计算的许用应力值447.85 MPa，该设计合理，满足结构设计要求。通过最终分析对比，可以预测该行星轮系在工作中最先出现破坏的是发生齿根断裂，接触压力带来的破坏要远小于齿根弯曲断裂带来的影响。

4 结论

(1)设计了具有四级增速的功率分流式行星结构5.5 MW增速箱，能够使得输入的大功率进行两路分流，有效降低齿轮承受载荷，减小整体体积。以第一级行星轮系为研究对象，建立了多体刚柔混合行星轮系有限元模型，采用Workbench 中Transient structural模块完成瞬态动力学分析。经过对比可知，有限元分析接触应力值130 MPa远小于许用接触应力值850 MPa，所以，设计的齿轮满足设计要求。

(2)通过对行星轮系的瞬态动力学分析，能够得到齿轮在运行过程中的应力随时间的变化关系，能够找出齿轮在运行过程中的薄弱之处，有利于对其薄弱之处进行修改，大大提高设计的可靠性，为大功率风电增速箱的设计提供理论和方法的支撑。