基于康复训练中力信号的人体参与度建模

耿安鸿，李伟达，李娟，张虹淼

(苏州大学 江苏省先进机器人技术重点实验室，江苏 苏州 215021)

0 引言

我国人口老龄化程度快速上升，脑卒中成为全球第二大、中国第一大致死性疾病[1]。偏瘫患者数量逐年递增，医学研究表明通过康复训练可逐步恢复或提高患者的步行能力，这使得康复训练机器人得到了日益广泛的研究和发展[2]。但在康复训练中，被动的训练对患者康复效果有限，而患者在主动参与康复训练时，康复效果显著提高[3]。因此，主动康复训练方法是康复训练机器人研究中的关键问题。

美国特拉华大学HAMNER S R等人对正向动态神经肌肉骨骼进行了建模[4]，提出基于肌电信号的肌肉活跃度算法，可以从肌电信号预测肌肉力的大小；燕山大学史小华等人通过采集下肢肌电信号，提取肌电信号的时域特征量，识别患者的运动意图，驱动康复机器人完成康复训练[5]。但由于肌电信号会受到空气湿度、电场等外部干扰以及肌肉疲劳、肌肉表面汗液等内部干扰，使得采集到的肌电信号不稳定，并且采集过程较为繁琐。因此，DUSCHAU Wicke A等人提出在康复训练中采用阻抗控制方法，在康复机器人的预期活动路径周围设置阻力，使得患者在预期路径内可以自由活动，超出范围时则会受到阻力[6]；哈工大李晓飞采用基于人机接触力的阻抗控制进行主动训练，实现了等助力或者等阻力的康复训练[7]。

上述研究可在一定程度上实现主动康复训练，但现有的方法无法对患者主动参与程度进行评估和量化，不利于实现患者的主动康复训练。

基于以上问题，本文提出一种基于人机接触力的人体主动参与程度评估模型，通过人与机器人之间的接触力获取人体的主动参与度，可为康复机器人应用中的主动康复训练提供基础。首先，利用人体肌电信息获取人体的肌肉活跃度，由于肌肉的活跃度可直接反映人体的运动状态，因此可建立肌电信息与人体参与度的关系；同时分析这一过程中人机接触力的变化，即可建立人机接触力与人体参与度的模型。这种方法可避免实际应用中的肌电信号干扰较大且准备工作复杂、使用不便等缺点，直接通过人机连接处的接触力获得人体的参与度，有很好的实用性。

整体建模流程如图1所示。

图1 人体参与度建模流程

1 康复训练实验系统

实验所用的床式下肢康复训练机器人模型如图2所示，其基于人体下肢髋、膝、踝关节的运动对应关系，进行了机构的多参数运动学优化，优化后的结构可模拟人正常的步态运动[8]。下肢康复训练机器人，安装有2个腿部连接机构与1个腰部连接机构，用于与人体连接。

图2 下肢康复训练机器人三维图

在腿部连接机构中，沿腿部轴向方向安装了2个一维力传感器，可测垂直于人体腿部方向的人机接触力，如图3所示。腰部连接机构内均匀分布着3个力传感器，可测垂直于人体腰部方向的人机接触力，如图4所示。

图3 腿部柔顺人机连接机构

图4 腰部柔顺人机连接机构

利用上述康复训练机器人，共进行了36组步态训练实验，其中9组主动跟随，18组半跟随，9组不跟随。主动跟随为实验者主动发力，跟随床体进行步态训练，半跟随为实验者处于半发力状态，不跟随为人体不发力，完全靠床体带动进行步态训练。使用其中19组用于参与度的建模过程，17组用于参与度模型的检验。实验系统如图5所示，同时采集了人体下肢相关肌肉的肌电信号以及腿部和腰部人机连接处的力信号。实验分类及实验数据组成如表1、表2所示。

图5 人体参与度建模实验系统

表1 实验分类 单位：组

实验分组实验分类主动跟随半跟随不跟随合计训练集数量59519测试集数量49417

表2 实验信号组成 单位：个

2 基于肌电信号的人体参与度建模

2.1 肌电信号采集

使用美国某公司MyoSystem-1400A型的表面肌电采集仪和MRMP 1.06 Master Edition软件对人体腰部及下肢肌肉进行肌电信号采集。

控制人体膝关节弯曲的主要有股二头肌、股薄肌、腓肠肌、缝匠肌、半膜肌与半腱肌; 控制膝关节伸展的主要有股直肌、股中肌、股外肌与股内肌。控制踝关节的主要为胫骨前肌。

电极片粘贴位置如图6所示。选择图6中的腰部肌肉2腰部多裂肌和右腿肌肉3股直肌，肌肉4股外肌，肌肉5股内肌，肌肉6胫骨前肌，肌肉15股二头肌，肌肉16腓肠肌[9]。

图6 电极片粘贴位置

2.2 肌电信号处理

原始的肌电信号为电压值，需要对采集到的肌电信号进行预处理，进行带通滤波去除低频噪声，此处采用四阶巴特沃斯滤波[10]， 对滤波后的肌电信号进行标准化；对标准化后的肌电信号进行低通滤波，由于肌肉中钙离子运动、肌肉动作电位沿肌肉的传输、肌肉和肌腱的粘弹性等情况，和这些相比，肌肉产生的力具有更低的频率。因此，为了使肌电信号与肌力相关，需要滤除高频分量。最后，利用微分方程求活跃度：

(1)

式中：X为肌肉活跃度；U为经过处理后的肌电信号；A为非线性形状因子，范围为0～-3，其中A= -3是高指数关系，A= 0是线性关系，此处取-3。

图7为人体主动发力跟随床体运动与不发力时的肌肉活跃度对比。肌肉开始运动的时候会剧烈放电，因此，从第2个周期开始对肌电信号开始分析。

图7 人体不同状态时肌肉活跃度对比

2.3 肌电信号权重分析

下肢运动中，主要有7块肌肉参与，因此需要对各肌肉的活跃度进行权重赋予，以获得总的下肢的活跃度。主成分分析法是一种客观赋权法，根据各指标间的相关关系或各项指标值的变异程度来确定权数,避免人为因素带来的偏差[11]。这里采用主成分分析法进行肌电信号的权重赋值。首先对n次实验的7个肌肉活跃度进行标准化处

理，可用以下矩阵表示：

(2)

对矩阵式(2)进行标准化处理：

(3)

求协方差矩阵Z并进行特征分解得

Z=UΛUT

(4)

得到Z的7个非负特征值λ1，λ2，…，λ7，这7个特征值即为主成分的方差，即

ΔZt=λi

(5)

定义λ1≥λ2≥…≥λ7，其中Λ为Z的特征值组成的对角阵；U为Z的特征向量按列组成的正交阵，构成了新的矢量空间，作为新变量(主成分)的坐标轴。

确定主成分个数：

(6)

当ηm>80%时，可认为主成分数目为m。

在本文中，经过计算，前两个主成分Z1与Z2贡献率相加为96.13%：

Z1=0.41X1+0.06X2+0.41X3+0.42X4+0.39X5+0.40X6+0.42X7

(7)

Z2=0.21X1+0.87X2-0.14X3-0.2X4+0.21X5-0.30X6+0.09X7

(8)

将式(7)与式(8)相加，得到整体肌肉活跃度M为

M=78.01Z1+18.12Z2=35.83X1+20.50X2+29.65X3+28.85X4+34.24X5+25.83X6+34.03X7

(9)

选择实验中肌肉活跃度最高的一组作为参与度100，最低的一组作为参与度0，建立基于肌电信号的人体参与度模型为：

YEMG=(M-min(M))/(max(M)-min(M))×100

(10)

将19组实验数据带入式(10)，结果如图8所示。

图8 基于肌电信号人体参与度建模

图8显示了19组实验数据的基于肌电信号人体参与度建模结果。

3 基于人机接触力信号的人体参与度建模

3.1 力信号采集与预处理

采集右腿2个力传感器以及腰部3个力传感器作为力信号原始数据，由于力传感器与固定支架之间为螺纹连接，存在预紧力，因此，每次实验前进行空载实验，记录空载时各力传感器信号作为初值。之后进行载人实验，人体受力即为载人实验的力信号减去初值。

由于减去初值后的力信号依然有各种噪声干扰，因此需要对减去初值后的力信号进行预处理。本文采用滑动平均滤波的方法处理力信号[12]，滤波效果如图9(本刊黑白印刷，相关疑问请与作者联系)。可以看出滤波后曲线平滑，较好地去除了噪声。

图9 滑动平均滤波前后对比

3.2 基于力信号的参与度模型分析与建立

腰部传感器始终支撑着人体腰部及上肢质量，取平均值并不能反映人体跟随程度，而腰部受力的波动情况则能很好地反映人体的跟随情况，在人体发力明显时，腰部受力会有较大波动；人体发力不明显时，腰部受力会有较小波动。因此，对腰部各传感器的力信号计算方差，作为参与度模型的3个输入量S1、S2、S3。

使用力信号进行参与度建模并没有数值参考，因此，力信号建模原理为使用力信号的4个输入量对肌电信号参与度模型进行拟合。假设肌电信号计算的参与度YEMG与力信号计算的参与度YF线性相关，将YEMG的0～100参与度映射到YF的0～100参与度，以均方根误差作为判定标准：

(11)

式中：σ为模型的均方根误差；YEMG为肌电信号计算的参与度；YF为力信号计算的参与度；n为建模所用的数据组数。

首先进行带有常数项的线性模型linear回归[14]， 回归结果为均方根误差7.95，判定系数0.72。带有常数项的线性模型linear回归误差较大，因此，尝试使用带有常数项、线性项和平方项的purequadratic模型进行回归，均方根误差为5.18，判定系数为0.92。两种回归效果如图10所示。可以看出purequadratic型建模更为接近基于肌电信号的参与度模型，误差更小，判定系数高。

图10 两种回归方法的参与度建模结果

因此，建模使用purequadratic回归所计算出的结果，即：

(12)

3.3 基于力信号的参与度模型检验

将测试集中的17组数据分别代入肌电信号模型式(9)-式(10)与力信号模型式(11)，计算人体主动参与程度，结果如图11所示。

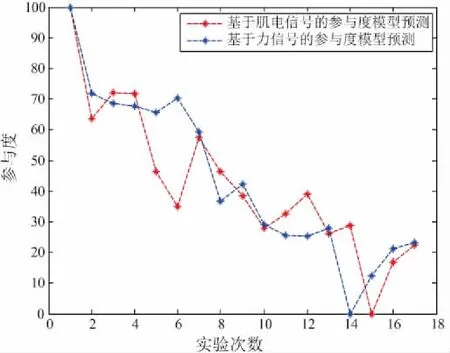
图11 两种模型预测结果

可以看出两种模型计算结果在个别组存在偏差，但整体趋势一致，因此，可在一定程度上评估人体的参与度，基于力信号的参与度模型具有一定的有效性。

4 结语

本文提出一种基于人机接触力的人体主动参与程度评估模型。首先，通过人体的肌电信号得到人体肌肉活跃度，建立人体参与度与肌电信号的关系。同时分析这一过程中人机接触力的变化，使用力信号对肌电信号得出的参与度模型进行拟合，得到基于人机接触力的参与度模型，并对此模型进行检验，检验结果两种模型计算的参与度接近，基于力信号的参与度模型具有一定的有效性。