适应不同重力环境的仿壁虎机器人运动仿真
刘琦,戴振东,王炳诚
(南京航空航天大学 航天学院,江苏 南京 210016)
0 引言
随着现代社会科技和经济的不断发展,越来越多的危险环境下需要作业,如核电站检测、油气罐壁面检查、空间站维修等,研制出能够代替人类进行危险作业的爬壁机器人成为了热点[1]。国外对爬壁机器人的研究如火如荼。美国斯坦福大学2011年提出了StickybotIII,采用基于肌腱的足部设计,能够对脚掌施加均匀负载,防止其过早脱落[2]。与竖直壁面上的爬行相比,爬壁机器人在天花板的爬行具有更大的难度,要求能在过驱动的情况下协调控制机体的运动和受力[3]。美国俄亥俄州立大学哥伦比亚分校研制的ACROBOT,可以在任何方位引力或完全零重力的表面攀爬,该机器人约1.5in宽,适合在狭窄的缝隙爬行,是用于检测国际空间站(ISS)内部和外部的原型[4]。国内对爬壁机器人的研究经过一段时间的发展,已取得一定的技术成果,部分技术已经实现产品化[5]。王田苗等人研制了采用柔性杆连接的磁吸附式仿壁虎机器人,能够在水平面和竖直表面爬行[6]。俞志伟等研制的干黏附材料仿壁虎机器人,能够实现在光滑竖直表面的爬行[7]。重庆大学提出了一种静电吸附式的仿壁虎机器人,在机器人的身体中心添加了1个旋转自由度,既能方便其转弯运动,又能消除部分由身体扭动造成的内部力矩[8]。
本文基于ADAMS仿真平台,围绕全方位三维空间无障碍运动仿壁虎机器人的研制,在已有机械结构的条件下,针对多关节冗余驱动下的运动稳定性、运动高效协调性等问题,开展了系统深入的研究。对仿壁虎机器人在不同重力环境下的运动进行了相应的仿真,基于机器人脚掌材料的黏附性能设计了足端轨迹,通过改变黏附力大小和运动步态等边界条件,得到适用于该机器人在不同重力环境下稳定爬行的静态平衡条件以及主要的干扰因素,提出在多关节冗余驱动下的稳定运动控制和高效协调运动控制的策略,将对仿生机器人技术的研究有着重要的指导意义。
1 方法
1.1 仿真对象
本文所仿真的对象是仿壁虎机器人样机[3],其三维结构如图1所示,机身尺寸为251mm×122mm×76mm;大腿长度46mm,小腿长度46mm,质量458g。机器人每条腿有3个自由度,分别由3个舵机驱动,作为抬腿、迈腿和外摆关节。脚掌处的球关节设计为机器人的每条腿增加了3个被动自由度,弥补了腿部舵机在空间上自由度的限制;各脚掌和球关节之间添加有复位弹簧作为脚掌的柔性结构,这一设计可以调节脚掌的刚性预压,使脚掌和接触面完全接触且预压相对均衡。

图1 仿壁虎机器人的三维结构模型
1.2 仿真过程
仿真环境中大地坐标系为O-xyz,x轴正方向为机器人的侧向,y轴正方向为机器人的法向,z轴正方向为机器人切向即前进方向。结合生物运动规律和机器人的机械结构特点,设计仿壁虎机器人在光滑表面上爬行所需的驱动数据:脚掌黏附力、足端轨迹和机器人运动步态。采用机械系统动力学分析软件ADAMS分别模拟重力为g、0、-g(g=9.8m/s2)的环境。测量机器人的运动学数据包括质心位移、抬腿高度等。动力学数据包括足端接触力等,作为评价机器人稳定运动的标准。
1) 脚掌黏附力
理论上在机器人脚掌施加黏附力可使机器人附着在爬行表面上,且脚掌产生的侧向力可以平衡由于机身扭动产生的惯性力[9]。在0重力和-g重力环境下模拟仿壁虎机器人的爬行时,需要在机器人的脚掌处人为施加载荷来模拟干黏附材料脚掌的黏附力。当脚掌与接触面接触时黏附力产生,当脚掌离开接触面时该脚掌的黏附力也随之消失。根据仿壁虎机器人实物所使用的脚掌材料聚乙烯硅氧烷(polyvinylsiloxane, PVS )的黏、脱附测试结果[10],可以抽象出抛物线来替代黏附力曲线。
2) 单腿足端轨迹
由于仿壁虎机器人的四肢分布具有中心对称性,因此可以将左右两侧对应的脚掌模型作统一分析。为获取机器人4条腿12个关节的转动角度参数,可以采用D-H参数法结合Matlab/SimMechanics工具箱搭建机器人单腿的
运动学逆解模型[11],只需产生1条前腿和1条后腿的关节角度,根据统一坐标系将数据进行对称计算。
根据脚掌黏附材料PVS法向黏附力较大、切向黏附力较小的特点[12]设计足端轨迹,再通过足端轨迹来逆解出各个关节所对应的角度。图2是一个分段式的足端轨迹规划,该分段函数中自上而下4个方程分别对应图中曲线的a、b、c、d部分,其中横轴代表足端在机器人前进方向的位移,纵轴代表足端在竖直方向上的位移,其分段函数表达式为:
(1)

图2 机器人足端运动轨迹示意图
3) 步态规划
机器人的步态规划可以简单认为是4条腿足端轨迹的规律性摆动的组合。机器人运动过程中,单腿在1个步态周期内抬起处于悬空时的状态称为摆动相,落下支撑机身时的状态称为支撑相;单腿支撑相时间占整个步态周期时间的比值称为步态占空系数;机器人的质心在1个步态周期内沿着机身前进方向移动的距离称为步距;腿在摆动过程中可以达到的最高高度称为抬腿高度。当步态占空系数在0.5左右时,机器人一般采用的是对角步态,当步态占空系数>0.75时,机器人一般采用的是三角步态。
壁虎在不同倾斜角度的表面爬行时,速度差异明显,且步态也不相同[13]。据此规划了仿壁虎机器人在不同重力环境下光滑平面上的爬行步态,其步态时序如图3所示。
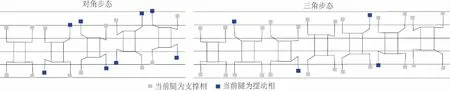
图3 对角步态和三角步态时序图
2 结果及分析

2.1 3种重力环境下对角步态的仿真
实验所设计的对角步态(占空系数df=0.6),运动周期T=5s,单腿跨距E=40mm,抬腿高度h=20mm。g重力下的仿真结果作为对照组,未在机器人脚掌施加法向黏附力曲线,0重力和-g重力下,分别采用峰值为2N和10N的抛物线作为机器人脚掌的法向黏附力曲线。仿真结果如表1。为了更直观地分析机器人运动的稳定性,选取机器人4个运动周期的质心位移曲线和左前脚的三维接触力曲线作运动学和动力学分析,如图4。

表1 3种重力环境下机器人采用对角步态的仿真结果

图4 3种重力环境下的对角步态仿真
从仿真结果可得,仿壁虎机器人在3种重力环境下爬行时,法向质心波动和侧向偏移量较小;前、后腿抬腿高度在3种重力环境下保持一致。g重力下,前、后脚掌法向接触力的平均峰值分别为2.25N和2.60N,略大于机器人的自重;0重力下,前、后脚掌法向接触力的平均峰值等于施加在脚掌的黏附力峰值;-g重力下,接触力的最大值比施加在脚掌上载荷的最大值少4.5N。此差值为每个对角脚掌平分的机器人自重以及脚掌的黏附力,侧向和切向的摩擦力与g重力和0重力环境下相比明显增大,实际上已经超出了当前脚掌面积的干黏附材料的承受能力,证明在-g重力环境下,仿壁虎机器人不适宜采用对角步态。
2.2 3种重力环境下三角步态的仿真
仿真所采用的三角步态(占空系数df=0.8),运动周期T=5s,单腿跨距E=30mm,抬腿高度h=20mm。0重力和-g重力下,分别在脚掌处施加了2N和10N的法向黏附力。仿真结果如表2、图5所示。
仿壁虎机器人在3种重力环境下爬行时,法向质心波动较小但质心偏移量很大。g重力下,各脚掌的法向接触力峰值约为机器人自重的1/3,接触力曲线不平滑,抬腿高度低,符合仿壁虎机器人匍匐爬行的姿态;0重力下,前、后脚掌的法向接触力大小接近所施加的黏附力大小2N,切向的摩擦力会随着黏附脱附过程发生波动,方向不固定。-g重力下,由于重力的拖拽,使得抬腿高度增大,步态的占空系数低于0.8;与使用对角步态在倒置表面的爬行情况相比,三角步态的法向接触力输出平均增加了1~3N,说明三角步态所需的法向黏附力确实比对角步态小,适合用作机器人在-g环境下的爬行步态。

表2 3种重力环境下机器人采用三角步态的仿真结果

图5 3种重力环境下的三角步态仿真
2.3 仿真局限性及合理性
在ADAMS仿真软件中柔性脚掌被默认为是刚体,因此脚掌与接触面开始接触或脱离的瞬间会发生刚体碰撞产生较大冲击力,使机器人脚掌的接触力曲线在开始黏附和脱附时刻会出现毛刺或者波动[14],并且由于黏附接触模块相关的仿真研究尚未有重大进展,本文仅定义了法向黏附力的大小,未定义脚掌切向和侧向的黏附力,仅依靠脚掌和接触面间的摩擦力无法满足机身不偏移。
机器人的运动协调表现为:质心无偏移、接触力曲线毛刺少、前后腿抬腿高度一致、足端在支撑相的速度方向一致等。本文中采用对角、三角这2种最主要的运动步态来进行机器人的步态规划,并统一以g重力环境下机器人的运动作为对照组。由结果可知,脚掌的法向黏附力对机器人自重带来的惯性影响起到了抵消作用,配合具有预压力的足端轨迹,机器人的运动稳定性得到了保障;同一运动条件下,对角步态在1个步态周期内的运动速率比三角步态高,为了在稳定黏附的基础上提升整机运动效率,机器人在g和0重力下更适用于对角步态,在-g重力下更适用于三角步态。
3 结语
本文主要研究了仿壁虎机器人在3种重力环境下稳定爬行的条件,根据生物学规律和机器人的结构和材料特性设计了脚掌黏附力、足端轨迹和步态,并基于ADAMS仿真平台的运动学和动力学数据,证明了设计的可行性和合理性,得到了机器人在不同重力环境下稳定运动时所需的条件,为机器人实物的足端轨迹设计、步态规划和脚掌结构设计提供了参考。

