基于对比度Harris的快速鲁棒图像配准算法

吴一全， 谢芬

(1.南京航空航天大学 电子信息工程学院，江苏，南京 211106;2.中国地质科学院 矿产资源研究所国土资源部成矿作用与资源评价重点实验室，北京 100037;3.成都理工大学 国土资源部地学空间信息技术重点实验室，四川，成都 610059;4.兰州大学 甘肃省西部矿产资源重点实验室，甘肃，兰州 730000)

图像配准是在不同条件下对同一对象获得的两幅图像校准的过程，这两幅图像可能取自不同的时间，源于不同的拍摄角度或不同条件的组合等[1-5]. 它被运用在遥感图像拼接、医学影像融合、运动估计等领域. 图像配准算法主要可分为基于区域的配准和基于特征的配准. 基于点特征的图像配准算法[6-8]因其计算速度较快、鲁棒性较强而受到关注. 其中基于Harris配准算法定位较为准确、计算速度也快、算法易于实现，但其有两个主要缺陷：① 不具有尺度不变性；② 需要事先根据经验设定角点检测的阈值，较大的阈值会使得角点数目检测得过少；较小的阈值则检测过多的角点，运算量很大，对后续图像配准造成不利影响. 为了解决基于Harris配准算法的尺度敏感问题，许佳佳[9]通过尺度不变特征变换(scale invariant feature transform, SIFT)描述Harris算法获得的角点进行配准. 该算法建立高斯尺度空间，使提取的角点具有尺度不变性，再使用Forsnter算法对角点进行精定位，但算法原理较为复杂. 高飞等[10]则提出了基于Harris-Laplace和信息熵的配准算法(entropy Harris)，然而该算法需要确定分块图像的信息熵，计算量较大，且每层图像角点检测的全局阈值和局部阈值都需要根据其所在尺度角点响应的局部极大值计算，这使运算量进一步增加. 另一方面，为了解决基于Harris配准算法的阈值自适应问题，现有的研究主要采取两条途径：提取图像显著性区域作为候选检测区域[11-12]；或根据区域显著性的不同自适应确定角点检测的阈值[13-15]. 李小昌等[11]计算分块区域的熵值，组成熵值矩阵，然后使用K-means算法根据熵值将熵矩阵分为3类，去掉熵值最小的一类，直接在显著性区域检测角点，但计算每块区域的熵值会耗费大量时间. 吴鹏等[12]首先使用区域检测算法构建图像的显著图，提取显著性区域作为候选检测区域，然后采用Harris算法检测角点，可进一步提高基于Harris配准算法的速度，但配准的精度有待提高. 何郴日等[13]使用谱残差理论确定每块区域的显著性，自适应地确定角点检测的阈值，但是谱残差计算复杂性较高. 周志艳等[14]提出了一种基于标准差Harris的配准算法(Std Harris)，依据图像像素灰度值的均值及标准差对其归一化，自适应地确定角点检测的阈值，但缺乏尺度不变性. 张见双等[15]提出了基于局部标准差Harris的配准算法(local Std Harris)，使得提取的角点分布均匀，但其配准的精度有待提高，对不同类图像配准结果差异较大，自适应程度较低.

鉴于上述不足，本文则提出了一种基于对比度Harris的快速鲁棒图像配准算法. 首先，将图像分为3×3个不重叠的块，依据中心像素与其邻域像素灰度值的差异计算每块图像的对比度，自适应地确定其角点检测的阈值，并通过“灰度相似性”删除伪角点；然后，使用Harris算法于建立的尺度空间上检测角点；接着，通过改进的归一化互相关(normalized cross correlation, NCC)对提取的角点粗配准；为了进一步加快剔除误配点的速度，先通过几何约束(斜率和距离约束)剔除一部分显著的误配点，再采用随机抽样一致性(random sample consensus, RANSAC)对剩余的点对进行精配准；最后，将本文算法与基于Harris的配准算法(Harris)、基于Harris-Laplace和信息熵的配准算法(entropy Harris)、基于标准差Harris的配准算法(Std Harris)以及基于局部标准差Harris的配准算法(local Std Harris)进行比较，验证本文算法的优越性.

1 基于对比度Harris的自适应角点检测算法

针对传统Harris算法对尺度敏感且需事先根据经验设定角点检测阈值的缺点，现提出一种基于对比度Harris的自适应角点检测算法. 首先，将图像分成若干块，计算每块的对比度，自适应地确定其角点检测的阈值；然后，依据“灰度相似性”，预先剔除伪角点；最后，构建尺度空间,并通过Harris算法提取角点. 算法流程图如图1所示.

1.1 自适应确定阈值及预先剔除伪角点

在对图像分块之后，按照中心像素与其邻域像素灰度值的差异计算每块图像的对比度，它表示该块图像的显著性. 根据计算所得每块图像对比度的不同即可自适应地确定角点检测的阈值. 对比度较小的区域设置较小的阈值才能检测到角点，而对比度较大的区域设置较大的阈值才不至于使检测的角点出现聚簇现象. 通过对比度自适应地确定块图像角点检测的阈值，可使得提取的角点数量适中，分布均匀. 文献[15]使用局部标准差自适应确定角点检测的阈值，使得检测的角点分布均匀，计算速度较快，但也存在不足之处：① 在块图像中采用同一像素均值计算标准差，如果块图像的像素灰度变化明显，会使计算出的局部标准差存在较大偏差；② 没有考虑图像的不同特性，仅根据经验选取统一的阈值参数. 对于特性不同的两类图像，会使在一类图像中检测到的角点分布均匀，而在另一类图像中检测不到角点或者出现角点聚簇现象. 现针对文献[15]方法的不足进行改进.

自适应阈值确定步骤如下.

Step 1 计算每块图像的对比度D.

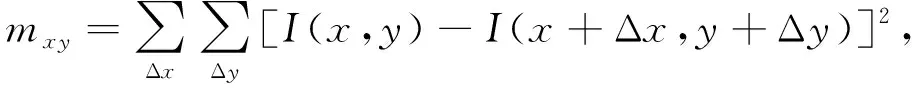
(-1≤Δx≤1, -1≤Δy≤1).

(1)

式中：I(x,y)和I(x+Δx,y+Δy)分别为中心像素灰度值和其邻域像素灰度值；h和w分别为块图像的高度和宽度.

Step 2 对块图像的对比度进行归一化.

(2)

Step 3 根据归一化对比度设置阈值.

(3)

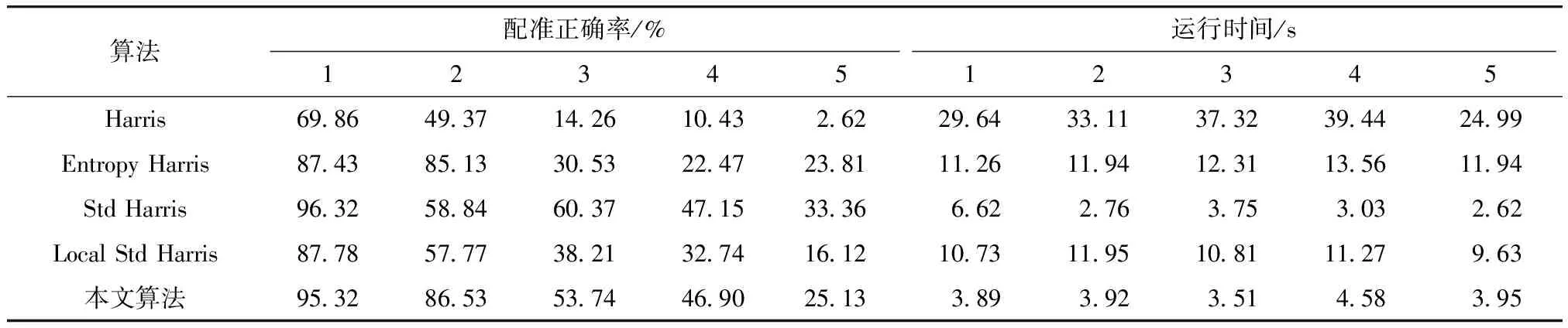
式中:0≤D≤1/2、1/2

为了减少后续角点检测时间，引入“灰度相似性”[16]，预先剔除部分伪角点. 将中心像素与其8邻域像素的灰度值I(x,y)和I(x+Δx,y+Δy)之差的绝对值，与预先给定的阈值T进行比较，若小于阈值即判定为相似点. 再依据中心像素邻域相似点的数目确定该中心像素点是否为角点.

(4)

(-1≤Δx≤1,-1≤Δy≤1且Δx≠0,Δy≠0).

式中，

d(x+Δx,y+Δy)=

(5)

当2≤N(x,y)≤6，此像素点为候选角点.

1.2 尺度空间中Harris角点检测算法

通过建立高斯尺度空间，使提取的角点具有尺度不变性. 文献[17]指出建立多层尺度空间耗费大量时间，本文结合其方法构建不同尺度的4层图像. 具体步骤如下.

Step 1 构建图像高斯尺度空间.

(6)

式中：“⊗”为卷积符号；I(x,y)为中心像素灰度值;G(x,y,sσn)为尺度因子sσn的高斯核;I(x,y,sσn)为与尺度因子sσn对应的尺度空间图像，s一般取0.7，σn=εσn-1，n=1,2,3，ε∈[0.6,1.2].

Step 2 计算角点响应函数(corner response function, CRF).

根据传统Harris算法的响应函数，得到尺度空间Harris算法的响应函数.

传统Harris算法通过计算窗口沿着不同方向平移后图像的灰度变化，寻找角点响应的局部极值来确定角点. 设中心像素(x,y)小窗口的平移量是(Δx,Δy)，其灰度值的变化c(x,y,Δx,Δy)为

c(x,y,Δx,Δy)=

∑wx,y[I(x+Δx,y+Δy)-I(x,y)]2=

(7)

式中:I(x,y)为图像像素灰度值；wx,y为加权函数；式(7)近似为

(8)

式中：Ix(x,y)和Iy(x,y)分别为I(x,y)在x方向和y方向的偏导数. 加入尺度空间后，将式(9)重新定义为

M(x,y)=(sσn)2G(x,y,σn)×

(10)

式中：Ix(x,y,sσn)和Iy(x,y,sσn)分别为I(x,y,sσn)在x方向和y方向的偏导数.

根据式(11)计算角点响应CRF,

CRF=det(M)-α(trace(M))2.

(11)

式中:det(M)为矩阵的行列式；trace(M)为矩阵的迹;α∈[0.04,0.06].

Step 3 在中心像素周围邻域内，计算其响应在局部的最大值；然后根据式(3)确定阈值Th，当局部的最大值比阈值大，将此中心像素点确定为候选角点；最后在尺度空间下，比较候选角点和其在相邻两尺度的局部响应，若候选角点的局部响应大，则为待配准角点，否则舍弃.

2 基于几何约束剔除显著的误配点

首先将原始图像减去其经过平滑滤波后的图像，补偿每幅图像的亮度差异，同时可以使得相关性运算速度加快，然后再根据改进的NCC[18]粗配准提取的角点.

INCC=

(12)

使用改进NCC粗配准后仍然会出现较多的误配点对，如果接着采用RANSAC[19]剔除误配点对，迭代次数较多，计算复杂度较大，也会严重影响配准正确率. 为此，在粗配准后首先依据几何约束去除掉一部分明显的误配点对后，再通过RANSAC算法精配准，减少参与RANSAC算法运算的数据量，提高其运行的速度及配准正确率.

几何约束(斜率和距离约束)具体步骤如下.

使用改进NCC配准后获得的Np对粗配准点对为

A={al=(pi,qj)},

i=1,2,…,m1;j=1,2,…,m2.

式中:al为基准图像及待配准图像第l组配准点对;l=1,2,…,Np；pi(xpi,ypi)、qj(xqj,yqj)分别为基准图像、待配准图像的配准点；xpi、ypi分别为pi的横、纵坐标;xqj、yqj分别为qj的横、纵坐标；m1和m2分别为粗配准后两幅图像的角点数.

Step 1 计算第l组配准点对斜率的大小.

(13)

式中|·|表示绝对值，l=1,2,…,Np.

Step 2 利用K-means将斜率大小分为3类，删除其中数量最少的一类.

Step 3 通过斜率约束后，计算基准图像、待配准图像配准点间的距离.

设经过斜率约束删选后的配准点对为

第lc组基准图像、待配准图像配准点间的距离为

(14)

Step 4 使用K-means将上述计算的距离分为3类，删除数量最少的一类.

3 实验结果与分析

为了验证本文提出的基于对比度Harris的快速鲁棒图像配准算法的优越性，进行了大量的实验. 首先给出基于对比度Harris的自适应角点检测算法的实验结果，并与Local Std Harris[15]进行比较；然后使用斯坦福大学提供的仿射协变特征数据集(affine covariant feature database)进行图像配准实验. 该数据集包括JPEG压缩(800×640)、图像模糊(1 000×700)、视角变化(1 000×700)、光照变化(900×600)、尺度变化(765×512)和旋转变化(800×640)等6种情况. 每种情况都有6幅变化程度不同的图像. 将本文算法与Harris、 Entropy Harris[10]、Std Harris[14]以及Local Std Harris[15]等4种同类配准算法进行对比实验. 实验环境：CPU为Intel Core i5-3210M 2.5 GHz，4G内存，64位Win10操作系统，Matlab R2016b.

为了体现本文提出的基于对比度Harris的自适应角点检测算法可以自适应地确定角点检测的阈值且使得提取的角点分布均匀，以3组矿产遥感图像为例加以说明. 图2(a)～(c)为文献[15]算法的检测结果，图2(d)～(f)为本文基于对比度Harris的自适应角点检测算法检测的结果. 文献[15]算法使用相同的阈值参数k检测上述3组图像的角点，而本文算法随着图像的不同自适应地确定阈值参数k. 由图2可看出，本文算法在不同类图像上检测的角点都分布均匀，而文献[15]算法对第1组图像检测的角点分布均匀，但对另外两组图像检测的角点仅分布在局部区域. 原因就在于，本文提出的算法使用尺度空间下角点的局部最大响应值作为阈值参数，而基于局部标准差 Harris角点检测算法使用固定的经验值作为阈值参数. 因此，本文算法自适应程度更高，检测效果更好.

下面针对斯坦福大学提供的仿射协变特征数据集中的6种情况进行图像配准实验和性能评价. 以配准正确率及运行时间为评价指标，验证本文提出的基于对比度Harris的快速鲁棒图像配准算法的优越性. 配准正确率R定义为

R=NR/NT.

(15)

式中:NT为粗配准点对数；NR为使用几何约束、RANSAC算法精配准后的点对数.

JPEG压缩、模糊、视角、光照、尺度和旋转变化图像与基准图像配准的正确率和算法运行时间列于表1～表7中. 表1是针对不同JPEG压缩程度图像与同一视场基准图像采用5种算法配准的正确率及运行时间对比结果. 由数据集中Jpeg压缩图像类可以看出，随着压缩程度逐渐加大，图像的颜色逐渐变暗，并有明显的像素斑块出现. 由表1可知，对JPEG压缩图像，5种配准算法鲁棒性都很好，且本文提出的算法所需运行时间最短.

表1 不同JPEG压缩程度图像与基准图像配准的正确率及运行时间

注：1～5表示JPEG压缩程度

表2 不同程度模糊图像(I)与基准图像配准的正确率及运行时间

注：1～5表示模糊(Ⅰ)程度

表3 不同程度模糊图像(II)与基准图像配准的正确率及运行时间

注：1～5表示模糊(Ⅱ)程度

表4 不同视角变化图像与基准图像配准的正确率及运行时间

注：1～5表示视角变化程度；“—”表示不能进行配准

表5 不同光照变化图像与基准图像配准的正确率及运行时间

注：1～5表示光照变化程度

表6 不同旋转变化图像与基准图像配准的正确率及运行时间

注：1～5表示旋转变化程度

表7 不同尺度变化图像与基准图像配准的正确率及运行时间

注：1～5表示尺度变化程度

表2和表3是针对不同程度模糊图像与同一视场基准图像采用5种算法配准的正确率及运行时间对比结果. 可以看出，Harris、 Entropy Harris、Std Harris以及Local Std Harris在图像模糊增大到一定程度时不能很好地配准，配准的正确率很低，而本文算法配准正确率虽然也会随着模糊程度增加而下降，但是仍然保持在相对较高的水平，且本文提出的算法运行时间相对其他4种同类算法具有明显优势.

表4是针对不同视角拍摄的同一视场图像采用5种算法配准的正确率及运行时间对比结果. 对于多视角图像进行配准需要检测局部视角不变的角点，本文建立尺度空间，在每层尺度图像上提取角点，并选取相邻尺度间局部响应的最大点作为候选角点，对于视角变化具有一定的鲁棒性. 可以看出Entropy Harris和本文算法对于视角变化的图像配准正确率较高，其他3种算法配准正确率很低，甚至不能配准; 同时，本文算法的运行时间非常短.

表5是针对不同光照拍摄的同一视场图像采用5种算法配准的正确率及运行时间对比结果. 可以看出，基于Harris的配准算法配准的正确率较低，其他4种算法对光照变化都有很好的鲁棒性. 光照变化可以建模为：像素灰度值I(x,y) 变换为aI(x,y)+b，后4种算法在计算过程中为了克服光照变化都对图像块像素灰度值进行了归一化，因此配准的正确率很高，而基于Harris的配准算法没有进行归一化，所以配准的正确率较低. 本文提出的算法和Local Std Harris运行时间较短.

表6是针对不同旋转角度的同一视场图像采用5种算法配准的正确率及运行时间对比结果. 图像旋转的角度分别为：5°,10°,30°,60°,90°. 可得出，各算法配准的正确率随着旋转角度的不断加大都在逐渐减小.

表7是针对不同尺度的同一视场图像采用5种算法配准的正确率及运行时间对比结果. Harris、Std Harris以及Local Std Harris没有建立尺度空间，提取的角点不具有尺度不变性，因此，当对存在尺度变化的图像进行配准时，正确率较低，甚至不能进行配准. Entropy Harris以及本文算法都是在尺度空间上检测角点，匹配的正确率较高，而且本文提出的算法整体运行时间最短.

由表1～表7可以看出，对于JPEG压缩、模糊、视角、光照、旋转及尺度变化图像，本文提出的算法整体配准正确率较高，运行时间较短，有明显优势. 其主要原因就是本文算法可以大幅减少配准的角点对数，角点数目减少比例平均可以达到50.98%，大大缩短了配准时间，而且本文提出的算法在尺度空间检测角点，鲁棒性较强.

4 结 论

本文提出了一种基于对比度Harris的快速鲁棒图像配准算法. 首先将图像分成若干块，依据对比度自适应地确定其角点检测的阈值，并通过“灰度相似性”剔除伪角点；建立高斯尺度空间，使Harris算法提取的角点具有尺度不变性；通过改进的NCC算法对角点粗配准，并采用几何约束(斜率和距离约束)和RANSAC算法对粗配准后的角点精配准. 大量实验结果表明，与Harris、Entropy Harris、Std Harris以及Local Std Harris相比，本文算法对于JPEG压缩、模糊、视角、光照及尺度变化图像具有较好的鲁棒性，配准正确率更高，自适应程度更强，而且可以大幅减少图像配准的时间.