基于单流道瞬态仿真的旋转流体机械伪集总叶片法研究

闫清东， 柯志芳， 魏巍， 李晋

(1. 北京理工大学 车辆传动国家重点实验室, 北京 100081; 2. 北方车辆研究所, 北京 100072)

液力变矩器是一种复杂的流体传动机械，同时也是液力机械传动中的重要组成部分. 主要由泵轮、涡轮和导轮三个部件组成. 有增扭变矩，吸能减振，在提高舒适性的同时延长传动部件的寿命的作用.

液力变矩器的工作与内部流体的工作状态密切相关，Dong等[1]早在1998年便开始使用高频五孔探针和高频测速装置测量并得到了液力变矩器内部大量的流场信息. 也有用压力探针传感器实验探究了汽车用液力变矩器内部的气蚀信号，并对所得流场的压力信号进行频谱分析，进一步得到了内部流场的相关信号均有规律振荡的规律；或使用非侵入式或者非接触式测量方法开展实验研究[2-3],李晋等[4]先后用激光多普勒速度计(laser Doppler velocimetry，LDV)开展了非接触式的变矩器内流场实验并获取了大量的变矩器内部速度场信息；此外Kubota等[5]用粒子图像测速法(particle image velocimetry，PIV)也成功开展对变矩器内部流场的实验探究,同样获取了内流场丰富的速度场信息. 通过以上的实验探究发现，变矩器内部流场的非稳态运动规律呈现较强的周期性，且流动状态与泵轮，涡轮以及导轮的相对位置有密切的关联，即存在较强的叶轮交互效应.

随着计算流体力学的发展，逐渐能够通过建立并解算变矩器内流场仿真模型来研究和解释叶轮交互效应在内的内流场复杂现象. 对于变矩器的流场仿真模型，目前主要有单流道仿真模型(SSM)和全流道仿真模型(FSM)[6]，前者通过模型周期性的特点，将不同叶轮的模型简化为含有单个或者几个叶片区域的流道模型；后者则为建立含有变矩器全部叶片的全流道模型，该模型能将叶轮交互效应对变矩器性能的影响考虑进去[7]，其计算结果的误差往往比单流道更低；但同等网格精度条件下，全流道模型的网格数量比单流道要多得多，并且全流道模型的网格质量更难控制，因此计算成本会高，更加复杂；此外，由于全流道模型结果对叶轮交互效应引起的各叶轮叶片的转矩等参数虽然有变化，但差别甚微，难以开展叶轮交互效应的深入研究[8].

为减小计算所需的时间和资源，同时保持非稳态流场仿真计算的精度，保留交互效应在内的内流场特征，本文提出一种基于单流道瞬态仿真模型的叶轮交互效应分析方法，以充分利用单流道瞬态仿真计算中的时序关系及其对应的不同叶轮空间位置关系对内流场特性深入研究. 此方法的结果最后与实验结果进行了对比，以保证该方法的准确性和可靠性.

1 仿真模型的建立

仿真模型为基于某一款循环圆直径为400 mm的液力变矩器开展，其泵轮、涡轮和导轮叶片数分别为ZP=22，ZT=24和ZS=20. 工作介质为CD15W40号高强度液压油，其80 ℃下的密度和动力黏度分别为860 kg/m3和0.019 Pa·s. 由于变矩器的工作温度的变化范围相对较窄，因此温度对其影响可忽略[9]，所以本算例不考虑温度的影响，即假设没有传热.

1.1 网格设置

该模型的单流道三维流场模型是由3D造型软件Pro/ENGINEER Wildfire 5.0完成，然后导入到商业软件ICEM CFD 15.0进行网格划分. 各流域的网格主要采用六面体结构化网格，流域的主要部位如图1所示.

最终的网格由372,550个元素和227,300个节点组成. 其他数量的网格也进行过计算，不过结果表明本算例所选用的网格是权衡计算精度和计算成本的结果如图2所示.

1.2 求解器设定

该算例采用的是非稳态不可压流场的瞬态CFD分析，边界条件主要如图1所示进行设定，交界面采用了Transient Rotor-Stator交界面模型，可探究不同叶片位置对变矩器结果产生的影响，节角则利用各叶轮叶片数量决定，算例采用的湍流模型为SST模型，可对湍流模型中的空化初生以及流场分离等流场特征进行高精度预测；此外采用隐式的二阶迎风格式对对流项进行解算[9]，收敛条件设置为残差(RSM)小于10-4，更小的残差会导致计算时间和计算成本的增加，而设定值对于转矩等参数的收敛已经足够，同理，单个时间迭代次数设置为10.

1.3 仿真时间和时间步长

表1 不同仿真工况下的主要参数，nP=2 000 r/min

Tab.1 Parameters for the different simulation conditions，nP=2 000 r/min

inT/(r·min-1)tP/mstT/msCPCTttot/s0.24001.3646.2555120.0750.48001.3643.12555240.0750.61 2001.3642.08355360.0750.81 6001.3641.56355480.075

为得到泵轮和涡轮相对导轮在不同位置时叶片的转矩值，在此将单个泵轮流道和单个涡轮流道进行等分，并用XPS和XTS分别表征泵轮叶片和涡轮叶片相对导轮的位置(如图3所示). 根据采样定理，采样频率需要大于最高被采集频率的2倍，工程实用采用2.5～3.0倍，而变矩器中存在的最高被采频率应为泵轮叶轮频率，即fmax=fPbmax=ZPnP/60，而采样频率为fs=XPSXTS/ttot≥fmax，由此可得XPSXTS>120.

此外为了使采样点在空间分布也更均匀，此处假设泵轮和涡轮中分布点的距离相等，即

(1)

上述边界条件下的方程(1)的最小可行解为XPS=12，XTS=11，其意义在于，XPS=0和XTS=0为初始位置，泵轮和涡轮单个流道分别等分为12和11个间隔点，最终间隔点分别为XPS=12和XTS=11的位置(如图3所示). 为遍历计算不同泵轮位置对应的涡轮位置上的变矩器流场结果，总时间步数应为XPSXTS=132，由此可得到时间步长应为Δt=ttot/(XPSXTS)=0.568 ms. 此时采样频率fs=1 760 Hz>2.4fmax，满足采样需求.

2 伪集总叶片法

2.1 单流道瞬态结果

单个叶片的转矩值可通过提取单流道瞬态仿真结果得到. 此处以变矩器设计工况点，即泵轮转速nP=2 000 r/min, 速比i=0.6为例进行说明. 该工况下由本文所提方法得到的泵轮、涡轮以及导轮单个叶片随时间的转矩值如图4所示. 可以看出各叶片转矩会有不同程度的波动，表现出强烈的振荡特性，这种振荡特性，正是由于泵轮和涡轮转动过程中相对导轮会发生相对位置的变化，不同位置上的转矩不同，因而导致这种周期性变化.

由于单流道仿真的结果只有单个叶片的转矩结果，假设同一个叶轮的不同叶片转矩一致，则可得到不同时刻下叶轮所受到的转矩值为

Tim,SSM(t)=ZTBl(t).

(2)

此种方法忽略了同一时刻叶轮中不同位置叶片相对导轮位置的影响，因此结果会有一定的偏差，下面介绍伪集总叶片法以改善此偏差.

2.2 不同相对位置下的状态结果

单流道瞬态仿真结果中得到了不同时刻各个叶轮上的单个叶片的转矩. 由泵轮、涡轮和导轮的转动角度及其时序关系，结合各自叶轮的节角大小，可确定泵轮和涡轮叶片相对导轮叶片不同位置时的转矩，进而再充分利该结果中所得的不同位置下的泵轮叶片转矩，最后可通过样条插值得到整个叶轮各个叶片的转矩，具体过程如下.

首先由单流道瞬态仿真结果可知，选定的泵轮和涡轮的叶片旋转角度分别为

(3)

式中：θP(t,j)，θT(t,j)分别为泵轮，涡轮叶片的旋转角度；t为时间；j为叶片编号. 根据瞬态仿真结果叶片的时序关系，可以确定其相对导轮的相对位置为

(4)

结合图3得到的各叶轮的转矩值与时间的关系，以及各个时刻内叶轮的位置关系，可以得到各叶轮的叶片转矩与相对导轮的不同泵轮位置XP及不同涡轮位置XT的关系：

(5)

以图4中的工况为例，式中求解得到的变矩器单个泵轮、涡轮和导轮叶片的转矩值分别如图5所示.

可以看出其转矩值与两个位置有较强的周期性和规律性. 通过样条插值可以得到任一时刻整个叶轮中第j个叶片的转矩TPB(j) 和TTB(j)：

(6)

对叶轮的不同叶片的转矩进行求和，即可利用单流道瞬态仿真结果，得到包含叶轮交互效应的变矩器叶轮转矩Tim,PLSM：

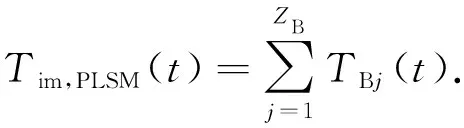
(7)

该方法中并非真实建立了全流道模型，而是利用单流道瞬态仿真结果，结合叶片相对导轮不同位置关系推导得到的“全流道”模型仿真结果，因此称为伪集总叶片法(PLSM). 此方法既能得到变矩器单个叶片的转矩值的脉动特性，同时又结合泵轮和涡轮叶片相对导轮叶片的相对位置的影响，对叶轮中不同叶片的转矩值进行精确求解，进而得到更加精确的叶轮转矩结果，不仅修正了单流道假设各个叶片转矩相等的而造成的偏差，而且又避免了全流道模型过高的求解成本，降低了设计难度.

3 结果与分析

3.1 伪集总叶片法结果

同时对各个速比工况下3个叶轮叶片的转矩均进行提取和整理，以其平均值为转矩基准值，以转矩的方差为转矩的波动指标，可得到不同速比工况下的各个叶片所受转矩的变化情况如图6所示.

可以看出，单叶片转矩中，涡轮和导轮所受转矩均随着速比的增大而减小，其中涡轮由97.9 N·m减小至32.0 N·m，导轮则从57.9 N·m减小至0.1 N·m，最高速比时已经接近耦合器工况；而泵轮则仅有小幅减小的趋势，从49.9 N·m小幅度减小到40.5 N·m. 此结果与稳态仿真结果以及实验结果相一致.

对于转矩脉动的幅度，随着速比的增加，泵轮单叶片扭矩的波动在计算时间内大幅降低，其方差由11.4降至1.3，表现出愈加平稳的趋势；而导轮有着相反的趋势，随着速度比增加，其波动值从1.4轻微增加至2.1，说明高速比下导轮内流场的不稳定性有所增加；涡轮与前两者表现都不太一致，在速比不大于0.6的情况下，涡轮的波动值基本保持不变，基本维持在4.3左右，而速比继续增加后，该波动值下降至2.5，也表现出高速比下扭矩值趋于稳定的特点.

通过PLSM中的方程可计算得到各个叶轮的所有叶片的转矩值. 仍以设计工况点，即泵轮转速nP=2 000 r/min，速比i=0.6为例，对单个工况的结果进行进一步分析，其各个叶轮转矩结果如图7(a)所示，与之对应的是由式(2)得到的SSM法各叶轮扭矩结果如图7(b). 与SSM的结果相比可以看出，PLSM得到的叶轮扭矩波动较小，几乎看不到的交互作用信息，说明叶轮内各个叶片的扭矩结果会产生综合作用，使得叶轮扭矩并没有太大的波动，这也说明全流道仿真结果并不适合用于叶轮交互效应的深入研究. 此外，在实际工作条件下，由叶片交互引起的扭矩波动与PLSM法得到的扭矩波动一样不明显，印证了本方法与实际更为接近，因此比SSM结果更准确、可靠.

3.2 性能对比

图8表明了两种方法得到的变矩比K和效率η与原始数据的对比结果. 结果表明，SSM和PLSM都过高预测了所有速度比的变矩比，但误差均小于5%. 随着速比的增加，SSM和PLSM的误差分别从3.81%下降到2.33%和从4.37%到1.66%. 整体而言，除了速比为0.2外，PLSM的变矩比误差均小于SSM的预测误差，表明PLSM对变矩比预测有着更高的精度；对于效率而言，SSM和PLSM同样也都过高预测了所有速度比下变矩器的效率，不过误差同样在5%以内.

对于泵轮转矩系数λ而言，PLSM和SSM对其预测结果与实验结果相差不大，不过由于SSM中转矩波动较大，使得SSM的误差范围大比测量结果大得多，PLSM则更小，如图9所示，与实验测量结果更为符合.

3.3 计算成本

计算结果表明，对于计算同一种工况的结果，PLSM采用的是和SSM一样的单流道模型，其计算成本要比全流道仿真模型(FSM)的小. 以计算速比为0.6，泵轮转速为2 000 r/min的工况计算结果为例，PLSM模型的网格数量仅为73万，而FSM模型的网格数量高达229万，使用同一工作站计算，前者耗时138.6 s，后者为189.1 s，可见PLSM方法比FSM方法计算成本更低.

4 结 论

基于D400变矩器的单流道瞬态仿真结果，针对不同泵轮和涡轮叶片相对导轮叶片的位置，会有不同转矩结果的现象，提出了PLSM方法来求解叶轮转矩以及变矩器原始特性，同时利用PLSM中包含的单流道叶片转矩的时域特性进行频域分析，以进一步分析变矩器的叶轮交互效应. 经分析论证，得到如下结论：

① 各个叶轮的单个叶片扭矩结果强烈依赖于泵轮和涡轮叶片相对于导轮叶片的相对位置，导致各叶轮的每个叶片以及整个叶轮的转矩会存在波动；

② 整体而言，SSM对预测不同速比下各叶轮转矩的变化趋势比PLSM具有更好的一致性，但PLSM法有着比SSM更高的精度，且误差均可在控制在5%以内，表明该方法可靠；

③ 计算成本方面PLSM比采用全流道模型的FSM有着更低的计算成本，更利于叶片的设计与快速评估，因此具有重要的理论指导与实践意义.