考虑测量噪声的车辆自适应巡航控制系统纵向跟车研究
黄菊花, 邹汉鹏, 刘明春
(南昌大学 机电工程学院,江西,南昌 330000)
车辆自适应巡航控制系统(adaptive cruise control,ACC)利用车载传感器探测前方行驶环境,并根据计算的期望值来自动调整车速,提高驾驶安全性和舒适性,被认为是最具商业化落地的辅助驾驶系统之一,可以显著改变动态交通环境[1-2].
目前,ACC控制系统的研究主要集中于跟踪性能、安全性能和舒适性能等方面. 上述性能主要通过前后两车的车速、加速度和两车之间的距离等参数进行评价. 控制算法方面包括PID、滑模变结构控制(sliding mode variable structure control,SMC)、模型预测控制(model predictive control,MPC)等主流算法,文献[3-4]中采用模糊PID控制器来调整前后车车速误差、间距误差等参数,系统响应迅速,动作灵敏,但是控制系统存在一定的振荡,鲁棒性不佳;文献[5-6]中采用改进型SMC实现自适应巡航控制,消除了传统SMC的抖动问题,系统具备良好的鲁棒性,但是,该控制算法未能同时优化跟踪性能、安全性能和舒适性能;文献[7-8]中采用MPC算法,优化了自适应巡航控制系统的跟踪性能、驾乘舒适性和燃油经济性等性能,系统具有良好的鲁棒性,但是未考虑真实驾驶环境中的测量噪声和环境干扰等因素. 在上述的研究中,真实驾驶环境中的测量噪声被忽略,可能导致所设计的控制器在真实驾驶环境中的控制效果不佳,降低ACC控制系统的性能,更有可能导致动态交通环境的恶化. 文献[9]针对带测量噪声的系统,设计状态观测器来估算系统状态,并设计反馈校正模型预测控制器对系统进行控制,该方法对本文所提出的存在测量噪声的自适应巡航控制系统值得借鉴.
基于此,为了提升带测量噪声的ACC的控制性能,本文设计卡尔曼滤波器对测量噪声进行滤波处理;采用反馈校正机制对跟车预测模型进行改进,降低参数不完全确定和外部干扰对模型精度带来的影响,并采用向量松弛因子对硬约束进行软化处理,避免优化求解过程中出现无可行解的情况;最后,将所设计的MPC控制器转化为带约束的二次规划问题,根据MPC滚动优化的特点,将控制量作用于被控对象,实现自适应巡航控制.
1 ACC系统纵向跟车动力学建模
ACC系统在跟车过程中,两车的间距误差、速度误差能够反映自车追踪性能的好坏,自车加速度是驾乘舒适性的重要指标. 综合考虑车辆和车间纵向动力学特性的耦合关系,建立如图1所示的纵向跟车动力学模型.
自车和前车运动学关系为
(1)
式中:Δd为前后车间距误差;Δv为车速误差;d、ddes分别为车间实际间距、期望车间距;vx、vpx分别为自车速度、前车速度.
本文中,采用固定车间时距,即
ddes=thvx+d0,
(2)
式中:th为车间时距;d0为静止车间距离.
自车期望加速度axdes到实际加速度ax之间,采用一阶时滞环节表示,时滞系数为τax,则
(3)

(4)
本文所建立的纵向跟车动力学模型,以自车期望加速度axdes为控制量,优化求解出期望加速度,并作用于实际车辆,实现自车的自适应巡航;因此,本文的重点就是求解存在测量噪声的ACC控制系统的自车期望加速度axdes.
2 反馈校正模型预测控制器设计
考虑车辆参数不完全确定、传感器测量噪声干扰的影响,本文采用如图2所示的基于反馈校正的模型预测控制器来处理真实环境中ACC系统纵向跟车.

2.1 卡尔曼滤波器
(5)
(6)
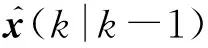
(7)
最后,根据式(8)计算当前最优状态估计的协方差P(k),用于下一时刻的迭代计算.
(8)

2.2 反馈校正跟车预测模型
受车辆参数不完全确定和外部干扰的影响,跟车预测模型与其实际状态之间不可避免地存在着一定的偏差,采用反馈校正法补偿跟车模型的预测误差,可提高跟车预测模型的鲁棒性.
定义k时刻跟车系统的状态与跟车预测状态之间的误差为
(9)
借助式(4)可得到
Bu(k-1)+Gd(k-1),
(10)

BΔu(k)+Gd(k)+He(k),
(11)
式中:Δu(k)为k时刻的控制增量;H为误差校正矩阵,且H=diag(h1,h2,h3).
借助式(4)、(11),可推导出以预测时域p、控制时域m的反馈校正跟车预测模型的矩阵形式:
Y=Sxx(k)+Suu(k-1)+SΔuΔu(k)+
Sdd(k)-Shx(k|k-1),
(12)
其中:
2.3 性能指标及I/O约束处理
为提高ACC的性能,本文考虑追踪性能、舒适性能、跟车安全条件这三类性能指标和约束条件.
① 追踪性能指标.
当前车稳态行驶时,车间间距误差和速度误差应该收敛于0,对该目标采用二次型表示为
JT=wΔdΔd2+wΔvΔv2,
(13)
式中:JT为追踪性能指标;wΔd、wΔv分别为间距误差、速度误差的权重系数.
前车动态行驶时,间距误差和速度误差应处于一个合适的范围之内,采用不等式约束来界定间距误差、速度误差的范围:
Δdmin≤Δd≤Δdmax,
Δvmin≤Δv≤Δvmax.
(14)
式中:Δdmin、Δdmax分别为车间距误差的上下界;Δvmin、Δvmax分别为速度误差的上下界.
② 舒适性能指标.
一方面,在跟车过程中,驾驶员期望缓加速、缓减速,从而保证乘坐舒适性,故采用输入的期望控制增量的二次型来定义舒适性的指标.
(15)
式中:JC为舒适性能指标;wΔaxdes为期望加速度增量权重系数.
另一方面,车辆实际纵向加速度、期望纵向加速度、期望加速度的增量保持在一定的范围之内:
(16)
式中:ax min、ax max分别为加速度数值的上下界;Δaxdes为期望加速度的增量;Δax min、Δax max分别为期望加速度增量的上下界.
③ 安全跟车条件.
综合碰撞时间(TTC)和固定安全车距设计的安全跟车条件为
d≥ds=max{tTTCΔv,ds0},
(17)
式中:ds为跟车过程中期望车辆间距;tTTC为碰撞时间;ds0为最小跟车安全距离.
综上,可得到如下的性能指标函数和约束条件:
J=JT+JC=wΔdΔd2+
(18)
(19)
(20)
d≥ds=max{tTTCΔv,ds0}.
(21)
对目标函数(式(18))进行预测型转化,可得
(22)
在本文中,式(21)为安全距离约束,该约束应当不予软化,以保证行车安全;式(19)(20)为舒适性和追踪性能的约束,适当放开该约束虽然会导致舒适性和追踪性能变差,但是不影响ACC系统的正常工作,因此,为避免出现无可行解的情况,这两个约束是可以适当放开的. 采用向量松弛因子对约束(19)和(20)进行软化,并进行预测型转化,可得
(23)
(24)
asy(k+i)≥
ds(k)-ddes(k),i=1,2…p.
(25)
式(23)~(25)中:
Δumin(k+i)=Δax min;Δumax(k+i)=Δax max;
umin(k+i)=ax min;umax(k+i)=ax max;
ddes(k)=τhvx+d0;
ε1≥0,ε2≥0,ε3≥为向量松弛因子;
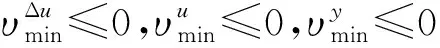

被软化的约束不能被无限放大,因此,在目标函数中增加代价函数,对松弛因子进行限制,即:
(26)
2.4 滚动优化
本节将2.3节中所建立的性能指标函数和约束条件,转化为带约束的二次规划问题;在k时刻求解出一系列控制量,并将控制量的第一分量作为实际的控制输入,作用于被控对象;在k+1 时刻重复上述过程,实现MPC控制器的滚动优化特性. 令:
Ep(k+1|k)=
R(k+1)-Sxx(k)-Suu(k-1)-
Sdd(k)+Shx(k|k-1),
则目标函数(26)可转化为
(27)
其中:
Γy=diag[QQ…Q];ΓΔu=diag[RR…R].
约束条件(23)(24)(25)转化为矩阵型为
(28)
式中:
Π=Sxx(k)+Suu(k-1)+Sdd(k)-Shx(k|k-1).
综上式(27)(28),优化问题转化为求解带有约束的在线二次规划问题,即:
(29)
在每一个采样周期内,利用式(29)进行MPC控制器求解得到一系列的控制输入增量和松弛因子
(30)
u(k)=Δu*(k)+u(k-1).
(31)
进入下一个采样时刻后,重复上述过程,通过在线优化求解将实现ACC控制系统的滚动优化.
3 控制系统仿真实验及分析
本文所设计的反馈校正模型预测控制器的参数见表1.
表1 反馈校正模型预测控制器参数
Tab.1 Parameters of feedback correction model predictive controller

参数数值参数数值th/s1.5υymax[0.010.010.01]d0/m5υymin[-0.01-0.01-0.01]tax/s0.355Δvmax/(m·s-1)2Ts/s0.1axmin/(m·s-2)-1.5p60axmax/(m·s-2)1.5m50Δdmin/m-5wΔd0.001Δdmax/m5wΔv0.001Δvmin/(m·s-1)-2wΔaxdes100γ-diag[111]tTTC/s-2.5Qdiag[0.050.020.001]ds0/m5Rdiag[0.180.151.00]υΔumin-0.01ξkξkΔdξkΔvξkax[]TυΔumax0.01ξkΔd0.01randn(1,1)υumin-0.01ξkΔv0.01randn(1,1)υumin0.01ξkax0.01randn(1,1)
为了验证本文所设计的控制器有效性和优越性,本节引入滑模变结构控制算法作为对比实验. 滑模变结构控制算法具有抵抗外界干扰、系统响应迅速等优点,文献[11]采用等速趋近律来设计滑模控制器实现自适应巡航系统的控制,但是,在稳态跟车时,加速度波动较大,降低了乘坐舒适性;因此,本文设计了基于指数趋近律离散滑模控制器来作为对比实验. 所设计的离散滑模变结构控制器的趋近律、控制率分别为式(32)~(34)所示.
s(k+1)-s(k)=-qTs(k)-
εTsgn(s(k)),
(32)
u(k)=-(SB)-1[SAx(k)-
(1-qT)s(k)+εTsat(s(k))],
(33)
(34)
离散滑模变结构控制器的具体参数见表2所示.

表2 离散滑模变结构控制器参数
3.1 前车急加速急减速工况

由图3、图4可知,三种控制方案都能够实现跟踪前车速度,前车加速或减速时,自车也能够快速地响应,跟踪上前车的速度,当前车稳态行驶时,速度误差最终收敛于0;由图5可知,采用MPC和KFMPC方法所得到的间距误差是优于KFSMC方法的,这提高了自车跟车安全性;由图6可知,KFMPC方法相比较于MPC方法,有效地减小自车实际加速的波动,这说明卡尔曼滤波器很好地滤除干扰信号,提升了控制系统的鲁棒性能,同时也提高了乘坐舒适性能;相比较于KFSMC方法,KFMPC方法使得自车加速度更加平滑,这有利于提高乘坐舒适性.
综上图3~图6,KFMPC方法在抵抗测量噪声方面比MPC方法更优,提高了控制系统的鲁棒性;KFMPC方法比KFSMC方法控制效果更优,提高了跟车安全性能与乘坐舒适性能.
3.2 dSPACE在环仿真实验
选取校园道路中的一段工况,用行车记录仪记录前车车速,导入到Simulink中,并基于dSPACE设计在环仿真实验,在环仿真实验结果如图7~图10所示.
由图7~8可知,三种控制方法都能够跟踪前车速度变化;由图9可知,KFMPC和MPC控制方法在间距误差控制方面,是优于KFSMC控制方法的,这提高了自车跟车安全性能;由图10可知,KFMPC方法相比较于MPC方法,有效地减小自车实际加速的的波动,这说明卡尔曼滤波器很好地滤除测量噪声,提升了控制系统的鲁棒性能,同时也提高了乘坐舒适性能;相比较于KFSMC方法,KFMPC方法使得自车加速度更加平滑,这有利于提高乘坐舒适性.
综上图7~10,采用KF MPC控制方法,在真实的校园环境中进行在环仿真实验,所得到的结果是优于其他两种控制方法的. 相较于MPC,KF MPC控制方法有效提高了控制系统的鲁棒性能和乘坐舒适性;相比较于KF SMC,KF MPC控制方法提高了自车跟车安全性能和乘坐舒适性.
4 结 论
本文考虑了存在测量噪声的车辆和车间纵向动力学特性的耦合关系,建立了纵向跟车动力学模型,基于该模型所选取的状态变量能够较好地反映ACC系统的控制性能.
所设计的卡尔曼滤波器能较好地消除噪声干扰的影响,并估算带测量噪声的状态变量;所设计的目标函数考虑了动态跟车、期望驾乘感受和跟车安全等约束条件,能较全面地描述车辆的跟踪性能和舒适性能;在基于反馈校正的模型预测控制中,将ACC控制算法转化为带约束的二次规划在线求解问题,所引入的向量松弛因子可有效避免优化求解过程中由硬约束导致的无可行解的情况,提高了求解最优结果的可靠性.
基于Matlab/Simulink,设计了对比实验,验证了本文的控制方法的有效性和优势性;基于dSPACE/Simulink设计了dSPACE在环仿真实验,验证了真实校园工况下,KF-MPC方法在跟车安全性、舒适性方面具有更好的优势.

