软聚类节点分裂层次模型

罗森林， 孙志鹏， 潘丽敏

(北京理工大学 信息与电子学院，北京 100081)

分类决策树算法，如ID3[1]、CART[2]和C4.5[3]，训练速度快，输出结果可解释性强，在实际生产生活中有广泛的应用. 但传统的节点分裂方法和判定方法，生成的模型存在结构冗余且过拟合等问题，限制了决策树算法判定效果的进一步提升，解决上述问题对于提高决策树性能具有重要的意义.

优化决策树节点分裂算法是提升决策树算法判定效果的有效途径. Deng等[4]对分裂属性添加了惩罚项，在保证分类精度同时降低了属性冗余度. Chandra等[5]DCM节点分裂方法，提高了分裂子节点中样本纯度，简化了树的结构. Hu等[6]将香农信息熵和优势粗糙集相结合，提出了排序互信息(rank mutual information，RMI)方法用于进行节点分裂，有效增强了决策树对次序类别数据的判别效果. 陈建凯等[7]优化了排序互信息计算方法，大大提高了决策树生成效率. 引入随机选择方法[8]或Tsallis信息熵[9]可以一定程度上缓解由于分裂算法贪心思想导致的局部最优解问题，提高模型效果.

此外采用组合模型方法也可以提升决策树判定效果. 利用bagging[10]或boosting[11]方法将多个决策树结合起来构成组合模型，可以克服单个树的过拟合问题. 采用模型树(logistic model tree，LMT)方法[12]，用逻辑回归模型替代决策树叶子节点，可以一定程度上缓解决策树不稳定且容易过拟合的问题.

通过优化节点分裂算法或改变树形结构的方式，可以有效地提升决策树算法效果，但是忽略了两个问题：①节点分裂每次在部分属性上采用线性方法实现，限制了对样本子空间的划分方式，需要多次分裂才能处理复杂的非线性分类问题，增加了模型结构的复杂度；②决策树采用硬分裂方法划分样本空间，由于决策树本身的树形结构，若上层节点划分出现错误，极易对最终判定结果产生影响，即存在误差迁移问题.

针对上述问题，本文提出了一种软聚类节点分裂层次模型(soft clustering node split hierarchical model，SCNSHM). 通过软聚类节点分裂方法对样本空间高效划分，有效精简模型结构，采用层次结构判别方法，将所有叶子节点处决策模型输出结果加权求和对新样本进行类别预测，有效缓解了决策树的误差迁移问题. 多组实验结果表明，本文提出的SCNSHM方法具备最高的F1值，且模型结构更为精简，泛化能力强.

1 算法原理

SCNSHM包括软聚类节点分裂、决策模型构建和层次结构判别3个部分. 其中软聚类节点分裂和决策模型构建用于训练层次结构模型，层次结构判别用于计算样本类别概率，原理如图1所示. 首先采用软聚类节点分裂算法替代传统决策树的节点分裂算法构建树形结构，然后在树形结构的各个叶子节点处分别训练决策模型完成层次结构模型构建，最后根据生成的层次结构模型，采用层次结构判别方法完成对新样本类别概率预测.

1.1 软聚类节点分裂

传统决策树在处理复杂非线性分类问题时，树形结构生成效率低下，存在结构冗余，容易造成模型过拟合. 使用聚类分析和支持向量机相结合的方法可有效提高分类准确性，降低训练复杂度[13]. 软聚类节点分裂方法结合了k-means和支持向量机(support vector machine，SVM)算法，学习过程中可以实现高效的非线性节点分裂，k-means聚类结果为SVM提供伪标签，对原数据中的标签噪声及错分样本进行修正.

软聚类节点分裂方法首先依据数据本身固有特点，利用k-means方法将数据聚拢成不同特点的聚类簇.k-means对数据的相似性大小度量计算公式如下：

(1)

式中:qik为第i个样本的第k维属性；qjk为数据集中第j个样本的第k维属性；dij为两样本间的欧式距离.

k-means只能将单个样本隶属于某个聚类簇，交界附近的样本容易被强行划分为某一聚类簇，这个问题通过计算样本属于不同聚类簇的概率来解决.

样本属于不同聚类簇的概率通过SVM方法计算. 假定训练集为

{(X1,y1),(X2,y2),…,(XN,yN)}.

然后采用SVM计算样本属于不同聚类类别概率.

SVM是一种最大化间隔分类器，目标是寻找可以分隔不同类别样本的分类超平面，同时该超平面满足最大化样本和超平面间隔的限制条件. 对于任意两个聚类类别构建SVM判定模型：

(2)

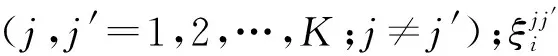
(3)

式中‖X-X′‖2表示两个向量之间的欧式距离，σ可以表示为

(4)

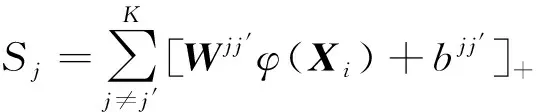
(5)

1.2 决策模型构建

根据生成的树形结构，在各个叶子节点处分别构建决策模型，可以在保证判别效果的同时，生成精简的层次结构模型，如图2所示.

叶子节点处决策模型均采用全训练集通过逻辑回归算法训练获得，训练过程中注意每个训练样本权重不同，结果表示当前节点下训练样本属于不同样本子空间的概率，如图2中样本Xi，在顶层根节点处软聚类节点分裂算法输出结果为g1(Xi,W)、g2(Xi,W)、g3(Xi,W)，分别表示样本Xi属于3个不同叶子节点的概率. 样本添加权重后的逻辑回归损失函数可以表示为

(1-yi)lg(1-hθ(Xi))].

(6)

其中β(Xi)表示样本权重大小，如图2中左侧叶子节点处样本Xi权重为

β(Xi)=g1(Xi,W).

(7)

hθ(Xi)为需要构建的决策模型即

hθ(Xi)=1/[1+exp(-θTXi)].

(8)

式中θ即为所求的逻辑回归决策模型中的权重系数.

最后依次对各个叶子节点构建决策模型的损失函数进行优化，完成层次结构模型的构建.

1.3 层次结构判别

层次结构判别从叶子节点出发，采用沿着层次结构模型向上计算的方式实现对新样本的预测. 如图3所示，在给定新样本Xj时，决策模型中输出其在不同叶子节点样本子空间下的为正样本的概率Pi(Xj,θi),i=1,2,3，非叶子节点输出结果衡量相应决策模型预测概率在最终预测结果中所占比重大小：gi(Xj,W),i=1,2,3. 决策模型输出预测概率与根节点软聚类分裂方法输出结果相乘求和,

2 实验及分析

2.1 实验目的

近年来机器学习方法被广泛应用到Ⅱ型糖尿病患病诊断中，Ⅱ型糖尿病患病与个体身体指标密切相关，其患病诊断是一个典型的复杂非线性分类问题，因此为了验证本文提出算法SCNSHM的判定效果，所有对比实验均在 Ⅱ 型糖尿病诊断应用上进行.

对比实验在两个数据集上实现，分别将SCNSHM与CART、C4.5和ID3决策树算法判定效果进行对比分析，说明SCNSHM在保证模型分类效果基础上可以有效精简模型结构.

2.2 评价指标

通过对比SCNSHM方法与其他决策树算法在糖尿病数据上的分类效果，验证方法的有效性. 其中分类效果采用F1-measure值作为评价指标为

(10)

式中:R为正样本召回率;P为正样本的准确率，其计算公式分别如下:

R=tp/N+,

(11)

(12)

式中：tp为预测正确的正样本个数；fp为预测错误的负样本个数；N+为真实正样本个数.

2.3 实验数据

实验数据为两组糖尿病数据，两组实验数据均包括性别(SEX)、年龄(AGE)、身高(HEIGHT)、体重(WEIGHT)、腰围(WAIST)、总胆固醇(CHOL)、甘油三脂(TG)、收缩压(SBP)、舒张压(DBP)、高密度脂蛋白(HDL)、空腹血糖(GLU)和负荷后血糖(OGTT)共12维属性，其中负荷后血糖属性为标签，负荷后血糖异常为正样本，负荷后血糖正常为负样本. 实验数据数据集1来源于美国国家健康与营养体检调查(national health and nutrition examination survey,NHANES)公开数据库，共6 497例样本，其中正样本1 186例，负样本5 311例；数据集2来源于北京医院老年研究所健康体检数据，共7 917例样本，其中正样本1 943例，负样本5 974例.

2.4 实验过程

实验将数据集随机均分为5份，选取其中4份作为训练集，采用5折交叉验证方法进行参数选择. 同时为了避免随机选择训练集对实验结果的影响，依次将5份数据分别作为测试集，其余数据作为训练集，利用参数选择获得的最优参数构建判定模型，并在测试集上测试模型判定效果.

模型超参数均采用网格搜索法系统地遍历多种参数组合，通过5折交叉验证获得最佳效果. 其中数据集1上SCNSHM方法参数为k-means聚类个数4，SVM判别模型参数C=0.1、γ=10；数据集2上k-means聚类个数5，SVM判别模型参数C=100、γ=100.

2.5 实验结果及分析

表1展示了两个数据集上对比实验结果，表2展示了在数据集1上，SCNSHM方法和CART方法所构建模型的最终判别规则. 实验结果显示，SCNSHM方法的判别效果在两个数据集的测试集上均为最佳，数据集1测试集上SCNSHM方法的F1值为0.53，比CART、ID3和C4.5的分别大15%、15%、6%；数据集2测试集上SCNSHM方法的F1值为0.38，比CART、ID3和C4.5的分别大27%、12%、8%. 在保证准确率的同时，SCNSHM方法显著提高了召回率，可以筛查出更多的糖尿病患病人群. 在模型结构方面，SCNSHM方法构建的模型均具有最精简的结构(其中数据集1上SCNSHM方法构建模型深度为2，叶子结点有4个；数据集2上SCNSHM方法构建模型深度为2，叶子结点有5个，与3个对比算法相比，明显精简了模型结构). 观察表2所展示的判别规则也可发现，SCNSHM方法构建的判别规则独立性更高，分裂间隔更大且更精简. 在相同算力情况下，训练过程的耗时增加主要由SVM的二次时间复杂度造成，但在模型的测试过程，其计算时间将仅由规则集的复杂度决定. 由此可知，SCNSHM方法在训练过程中，软聚类节点分裂将一定程度上提高模型训练的时间成本，但在测试及应用过程中，模型相较对比算法具有更快的判别速度.

表1 对比实验结果Tab.1 Results of contrast experiment

注：F1为F1-measure值；L为模型结构深度；n为模型叶子结点个数

表2 NHANES数据集模型复杂度对比Tab.2 Comparisons of model complexity on NHANES dataset

注：规则按照符合该条规则的样本数量排序

SCNSHM方法具有最高的F1值且模型结构最精简，在各个叶子节点处构建决策模型，采用层次结构判别方法，将不同叶子节点输出判别概率加权求和，即使上层节点出现判别错误时，仍然可以通过其他叶子节点的输出结果进行补偿，因此可以有效避免出现误差迁移问题，有效提高模型判别效果.

3 结 论

本文提出的SCNSHM方法通过软聚类方法进行节点分裂，在叶子节点构建决策模型，并利用层次结构判别方法对样本进行加权预测，克服了决策树算法结构冗余、误差迁移的问题. 具体来说，首先利用k-means对样本进行聚类，以聚类类别为伪标签构建SVM模型进行分类，构建层次结构模型，然后依据所得层次结构模型，计算样本权值，在叶子节点处训练逻辑回归模型，完成判定模型的构建，最后利用层次结构判别方法实现对新样本的预测. 经过实验表明，SCNSHM相比于CART、ID3和C4.5算法，在更精简的结构上实现了更好的分类效果.