数形结合思想在数学教学中的应用


【摘要】本文论述数形结合思想在小学数学课堂教学中的应用策略,提出应用数形结合思想实现数学知识的真理解,促进数学知识的深思考,突破数学知识的实障碍以及引发新体验等教学建议。
【关键词】小学数学 数形结合 数学思考
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2020)02A-0141-02
“数”和“形”是学习数学、研究数学最重要的两个元素,也是学生学习数学的基础。通过具体的“形”,可以帮助学生理解抽象的“数”,达到以形助数以形解数的目的。在以往的课堂教学中,一部分教师割裂数形之间的关系,影响了知识内化的进程,给学生的数学学习带来了困难,无形之中挫伤了学生学习数学的热情,打击学生学好数学的信心,甚至让学生产生厌烦的心理,这极不利于学生的发展。因此,教师应遵循学生的认知规律和学习需求,将抽象、深奥的数学知识变成可视、可感的事物或图形,丰富学生的感性经验,让学生获得清晰的表象,进而学会数学思考。
一、数形结合实现“真理解”
算理和算法是计算教学相互依存、相互促进的两个方面。算法是具体的计算方法,重在解答“怎么算”的问题,而算理是对算法的解释,重在解答“为什么这样算”的问题。学生对算理的理解难度较大,需要感性经验的支撑,教师可以利用数形结合的方法,让学生经歷“具象化”“形象化”和“再创造”的过程,实现对算理的深层理解和对算法的正确掌握,更好地提升学生的计算能力,为后续学习数学奠定坚实的基础。
在教学《两位数减两位数的退位减法》时,教师出示例题:操场上有55名男生和19名女生在跳绳,跳绳的男生比女生多多少人?学生依据题中的数量关系列出算式55-19,但在竖式计算时应该怎么算学生难以理解。于是,教师让学生拿出小棒进行操作,引导学生将摆小棒的过程与列竖式计算的过程有机结合,从而帮助学生更好地理解笔算退位减的算理。首先拿出5捆小棒和5根小棒,然后从中拿去1捆小棒和9根小棒,学生在拿的过程中发现5根减9根不够减,只好拆开一整捆小棒,将10根小棒和原先的5根合起来,用15减9等于6。也就是说5减9不够减时,应向十位退一当10,与5合起来是15,15减9等于6,在个位写6,剩下4捆减1捆,等于3捆(即4个十减去1个十,得到3个十),在十位写3,合起来是36。显然,这样的教学过程,有助于丰富学生的表象,让学生对算理的理解更加透彻,记忆更加深刻。
上述案例,教师巧妙设计“拿”小棒的过程,让学生明确了“从十位上退1”的原因和“十位上少了1”的道理,真正让学生在操作中明理,在明理中成法。
二、数形结合促进“深思考”
数学中的公式、定义、规律等内容表述严谨而抽象,学生很难透彻理解,影响了数学知识体系的构建。例如,在进行“空间与几何”相关内容的教学时,教师可以渗透数形结合思想,让学生更加深入地探究图形的知识,实现数与形的转化,让难以理解的数学知识变得简单、明朗,进而强化学生对所学知识的理解,提高学生的数学综合能力。
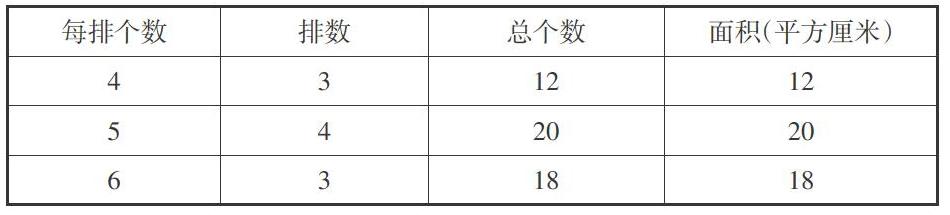
在教学《长方形和正方形的面积》时,教师让学生用边长1厘米的小正方形拼成长方形,然后观察所拼成的长方形中一排摆了几个,摆了几排,它的面积与所拼长方形的长、宽之间有什么关系。有的学生一行摆了4个、摆了3排;有的学生一行摆了5个、摆了4排;还有的学生一行摆了6个、摆了3排……于是,教师引导学生将相关的数据整理到下面的表格中:
接着教师让学生观察表格,看有什么发现。学生发现每排有几个,长方形的长就是几厘米,有几排,长方形的宽就是几厘米,总个数是多少,面积就是多少平方厘米。在此基础上,教师再让学生思考如何计算长方形的面积。因为学生有了先前的感性认识,所以他们很快发现长方形的面积是每排个数与排数的乘积,顺利地推导出长方形的面积计算公式:长×宽。这样的学习过程,充分尊重了学生的学习需求,通过数形结合,让学生利用小正方形拼长方形的方式进行探究,促进了学生的深入思考,无形中提升了课堂教学效益。
三、数形结合突破“实障碍”
数学是一门研究“数”与“形”的学科,而数轴是体现数形结合思想的重要内容,所有的有理数,在数轴上都可以找到唯一的点与它相对应,形成由小到大的数列。借助数轴,可以把“数”与数轴这个“形”有机地融合在一起,使抽象的数变得有形可依,从而帮助学生更好地发现数与数之间的内在关系。例如,在教学比较数的大小时,教师可以引导学生利用数轴来比较,从而帮助学生更好地建立数感,培养学生的数学综合能力。
在教学负数的相关知识后,教师让学生比较以下几组数的大小:①-3和0;②2和-5;③-3和-1。第①、②组,学生依据所学知识“正数都大于0,负数都小于0”,轻松地得出了结果。但比较“-3和-1”时,很多学生都认为-3>-1,显然学生受旧知识的影响,产生了“负迁移”。此时,教师并没有马上给予评价,而是利用数轴来帮助学生理解:
学生依据数轴上数的排列特点,右边的数总比左边的大,越往左,数就会变得越来越小,而越往右,则数越来越大。由数轴可知,-1在数轴上位于-3的右边,所以-1>-3。这样的教学过程,将原本抽象的数化成直观的图形,这样在无形之中降低了学习难度,帮助学生深刻地理解并掌握了比较两个负数大小的方法,体验了数形结合的价值。
四、数形结合引发“新体验”
尽管“形”具有形象、直观的优势,但也有不足之处,那就是不便于表达。在数学课堂中,很多学生在学习平面图形的相关知识时经常产生混淆,也有学生表现为学习新的图形知识后,再现旧知时容易出错,出现负迁移的现象。面对这样的教学现状,教师可以将复杂的“形”用简洁的“数”表示出来,问题就会变得简单、明了,从而让学生更好地体验“数”的抽象化魅力,更好地区分易混淆的概念,进而更准确、严谨地把握好“形”的特点。
在教学长方形和正方形的面积后,很多学生有这样的认知:面积大的图形,周长一定大;周长大的图形,面积一定大。显然这是不对的,其原因在于学生没能正确区分周长和面积的本质内涵。于是,教师安排了以下的体验活动:用12个边长1厘米的小正方形拼成长方形,可以怎样拼?周长和面积分别是多少?汇报时,列出下表:
然后让学生观察表格后认真思考:这3个长方形,什么相同?什么不同?为什么?在学生交流后,教师抛出这样的问题:用长16厘米的绳子,围成长和宽都是整厘米的长方形,可以怎样围?周长和面积分别是多少?汇报时,列出下表:
待学生汇报后,教师让学生观察表格,然后说一说有什么规律。这样的学习活动,让学生在体验中认识到:周长与面积是不同的两个概念,周长长,面积不一定大,周长相等,面积也未必相等。
上述案例,在学生的认知出现错误时,教师通过数形结合的方式,加强学生的体验,让学生在体验过程中触及概念的本质,使学生的认知从模糊走向清晰,更好地加深了对所学知识的理解。
总之,数形结合可以将抽象思维和形象思维有机地结合起来,实现抽象的数学知识和具体形象、表象之间的转化,灵动学生的思维。教师应注重数形结合思想的挖掘,使得“数量关系”与“空间形式”珠联璧合,真正扬“数”之长,取“形”之优,推动学生实现可持续发展。
作者简介:翁瑜梁(1974— ),女,广西浦北人,大学专科学历,一级教师,钦州市道德模范先进个人,主要研究方向:小学数学教育教学。
(责编 林 剑)

