等时降线问题的求解*
邢家省,吴 桑
(1.北京航空航天大学数学与系统科学学院,北京 100191;2.数学、信息与行为教育部重点实验室,北京 100191)
多位数学家对等时降线问题或等时降落问题[1-4]进行了原创性的研究.历史文献中,关于等时降线问题的解法都较复杂,限制了其广泛传播,因此有学者[5-6]充分利用现代成果给出了严密简洁的解法.笔者拟将质点沿光滑曲线从一定高度下滑所需时间的问题[3,7-8]转化为积分方程求解的问题,并对积分方程做阿贝尔积分变换,再利用积分换序方法进行求解.
1 质点沿光滑轨道下滑所需时间
建立xOy坐标系,Ox轴正向水平向右,Oy轴竖直向上,设A点坐标为(x1,y1),B点坐标为(x2,y2),x1 或者 设曲线L的最低点在Ox轴上,质点在曲线L上高度为h处从静止开始下滑,到最低点所需时间[3-8]为 (1) 设常数H>0.实际降线问题是从有限高度下落的,所以降线问题可归结为如下积分方程和微分方程问题[1-4]: (2) 积分方程问题是给定函数T(h),寻找函数f(y),使得(2)式成立.(2)式被称为阿贝尔积分方程[1,4]. 则有 h(x)=g(x) 0 证明对于任意固定的0 由于φ(x),f(x)∈C(0,H],且在(0,H]上可积,因此 由于 因此 证明 证毕. 引理3[5-6]设f(x)在(0,H]上连续可积,令 (3) 则有 证明对(3)式两边作阿贝尔积分变换[4-6],利用引理1的结果可得 利用引理2的结果可得 证毕. 引理4[5-6]设f(x)在[0,H]上一阶导数连续,且f(0)=0,令 φ(0)=0, 则有:(ⅰ)φ(x)在[0,H]上一阶导数连续,且 φ′(0)=0. 证明(ⅰ)当0 由于当0 再令 利用引理1的结果可得h(x)=g(x),0 利用引理2的结果可得 于是 从而 证毕. 显然,引理3比引理4的条件少,利用引理3更容易解决等时降线问题. 等时降线的积分方程的求解,即T(h)为常数T时的求解.此时,积分方程为 (4) 对(4)式利用引理3 的结果,可得 (5) (5)式就是积分方程(4)的解. 在等时降线情况下,利用(3)式可得如下常微分方程: (6) 令t=2θ,则有 这正是倒摆线的方程形式.由此可知,等时降线是倒摆线[1-8].文献[2]中对倒摆线具有等时性给出了计算验证. (7) 积分方程的问题是给定函数T(h),寻找函数f(y),使得(7)式成立.(7)式被称为阿贝尔积分方程[1,4].阿贝尔运用拉普拉斯变换方法[1,4]给出了(7)式的求解过程. 利用广义积分的计算方法[9-18]可得 所以 由于 因此由拉普拉斯变换的性质[8-12]可得 (8) (8)式即为(7)式的求解公式. 当T(h)=T(T为常数),也即等时降线情形时,利用(8)式可得 于是 从而得到等时降线情形的微分方程 (9) 对(9)式进行求解,可知等时降线是一条倒摆线.2 质点从有限高度下落的降线问题的阿贝尔积分方程
3 有限区间上的阿贝尔积分方程的求解
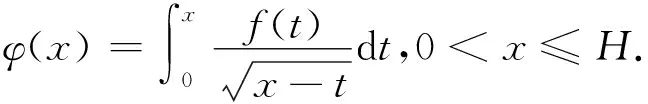
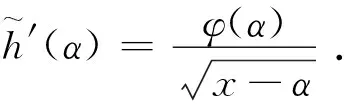


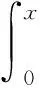
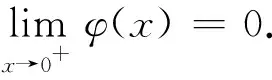
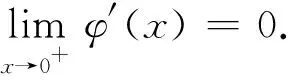
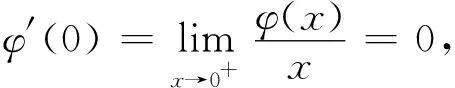
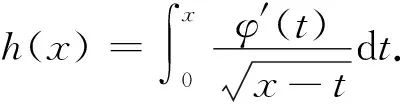

4 等时降线的阿贝尔积分方程的求解
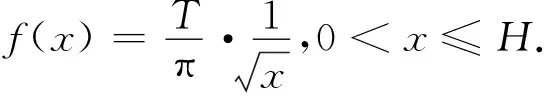
5 等时降线是倒摆线的证明
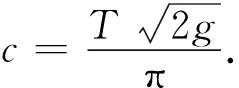
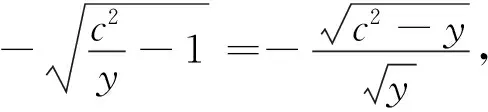

6 阿贝尔关于等时降线问题的求解



