含参DC复合优化问题值函数的Fréchet次微分*
肖程凤,胡玲莉
(吉首大学数学与统计学院,湖南 吉首 416000)
1 问题的提出
约束优化问题在最优化理论中占重要地位.许多学者研究了目标函数是凸或DC函数、约束条件是任意多个(可能无限)凸或DC不等式的约束优化问题,得到了相应的Farkas引理、Lagrange对偶及最优性条件等结论[1-6].
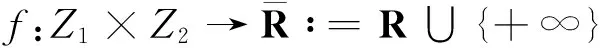
(1)
其中几何约束为
F(x)∶={y∈Y:(x,y)∈C},
(2)
不等式约束为
G(x)∶={y∈Y:ft(x,y)≤0,t∈T}.
(3)
当φ为单位算子时,Dinh等[6]在f,g,ft(t∈T)是下半连续函数、C是闭集的情况下,通过闭性条件建立了含参DC优化问题值函数的Fréchet次微分的上估计;方东辉等[7]在函数不一定下半连续、集合不一定是闭集的情况下,利用弱于文献[6]中闭性条件的约束规范条件建立了值函数Fréchet次微分的上估计.受这些研究的启发,笔者拟引入新的约束规范条件,建立(1)~(3)式中定义的值函数的Fréchet次微分的估计式.
2 记号与定义
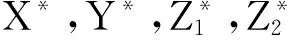
Z⊕∶={x*∈X*:〈x*,x〉≥0,∀x∈Z},
凸子集D在点z0∈D的法锥定义为
N(z0;D)∶={x*∈X*:〈x*,z-z0〉≤0,∀z∈D}.
对于X上的子集族{St:t∈T},约定∩t∈ØSt=X.
设f是X上的广义实值函数,定义f的有效定义域、上图和共轭函数分别为
domf∶={x∈X:f(x)<+∞},
epif∶={(x,r)∈X×R:f(x)≤r},
f*(x*)∶=sup{x*,x-f(x):x∈X} ∀x*∈X*.
显然,epif*是弱*闭集.当f是凸函数时,f在点x∈domf的次微分定义为
∂f(x)∶={x*∈X*:f(x)+〈x*,y-x〉≤f(y),∀y∈X}.
当∂f(x)≠Ø时,称f在点x次可微.特别地,由法锥定义可知N(x;Z)=∂δZ(x),∀x∈Z.一般地,f∶=f(x,y)在点(x,y)相应的偏次微分分别表示为∂xf(x,y)和∂yf(x,y).设Ω⊆X×Y,点(x,y)∈Ω,则法锥N(x;Z)相应的投影分别为
NX((x,y);Ω)∶={x*∈X*:∃y*∈Y*s.t.(x*,y*)∈N((x,y);Ω)},
NY((x,y);Ω)∶={y*∈Y*:∃x*∈X*s.t.(x*,y*)∈N((x,y);Ω)}.
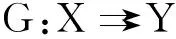
domG∶={x∈X:G(x)≠Ø},
gphG∶={(x,y)∈X×Y:y∈G(x)}.

φ(tx1+(1-t)x2)≤Ktφ(x1)+(1-t)φ(x2),
则称函数φ是K-凸函数.设φ:X→R∪{±∞}是实值延拓函数,x0∈domφ且满足|φ(x0)|<+∞.根据文献[8],定义φ在点x0的ε次微分为
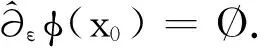
(4)
3 值函数Fréchet次微分估计
设

M(x)∶={y∈F(x)∩G(x):μ(x)=(f∘φ)(x,y)-g(x,y)}.
若无特殊说明,均假设dom(f∘φ-g)∩A≠Ø,domM≠Ø.用T(x0,y0)表示点(x0,y0)∈X×Y的活动指标集,即T(x0,y0)∶={t∈T:ft(x0,y0)=0}.定义(x0,y0)∈gphM和y*∈Y*的KKT乘子集为
(5)
为了研究含参DC复合优化问题的值函数的Fréchet次微分的上估计式,引入以下约束规范条件:
定义1(ⅰ)设点(x0,y0)∈dom(f∘φ-g)∩A,若
(6)
则称系统{f,φ,g,δC;ft:t∈T}在点(x0,y0)满足F-(BCQ)条件.
(ⅱ)设点(x0,y0)∈A,若
则称系统{δC;ft:t∈T}在点(x0,y0)满足(BCQ)条件[9].
(ⅲ)设点(x0,y0)∈A∩φ-1(domf),若
(7)
则称系统{f,φ,δC;ft:t∈T}在点(x0,y0)满足(CBCQ)条件[10].
引理1[10]假设存在点(x0,y0)∈φ-1(domf)∩intA,使得f在φ(x0,y0)处连续,或存在点(x0,y0)∈φ-1(domf)∩A,使得f在φ(x0,y0)处连续且φ在(x0,y0)处连续.若系统{δC;ft:t∈T}在点(x0,y0)满足(BCQ)条件,则系统{f,φ,δC;ft:t∈T}在该点满足(CBCQ)条件.
命题1设(x0,y0)∈A,若系统{f,φ,δC;ft:t∈T}在点(x0,y0)满足(CBCQ)条件,则系统{f,φ,g,δC;ft:t∈T}在该点满足F-(BCQ)条件.
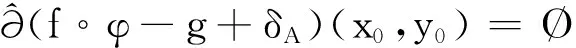
又(7)式成立,故
于是(6)式成立,结论得证.
由引理1和命题1可得以下推论:
推论1假设存在点(x0,y0)∈φ-1(domf)∩intA,使得f在φ(x0,y0)处连续,或存在点(x0,y0)∈φ-1(domf)∩A,使得f在φ(x0,y0)处连续且φ在(x0,y0)处连续.若系统{δC;ft:t∈T}在点(x0,y0)满足(BCQ)条件,则系统{f,φ,g,δC;ft:t∈T}在该点满足F-(BCQ)条件.
定理1若系统{f,φ,g,δC;ft:t∈T}在点(x0,y0)∈gphM满足F-(BCQ)条件,则对于∀γ>0,有
(8)

μ(x)-μ(x0)-〈u*,x-x0〉+γ‖x-x0‖≥0 ∀x∈x0+ηB.
(9)
注意到点(x0,y0)∈gphM,则有μ(x0)=f(φ(x0,y0))-g(x0,y0).对于任意点(x,y)∈A,有μ(x)≤f(φ(x,y))-g(x,y).结合(9)式可知,对于任意点(x,y)∈A∩((x0+ηB)×Y),有
f(φ(x,y))-g(x,y)-f(φ(x0,y0))+g(x0,y0)-〈u*,x-x0〉+γ‖x-x0‖≥0.
(10)
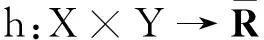
h(x,y)∶=f(φ(x,y))-g(x,y)-〈u*,x-x0〉+γ‖x-x0‖,
则由(10)式可知
h(x0,y0)≤h(x,y),∀(x,y)∈A∩((x0+ηB)×Y).
由(4)式可得
(11)
注意到点(x0,y0)是集合(x0+ηB)×Y的内点,故该集合的示性函数在点(x0,y0)连续,从而
(12)
根据函数h的定义和文献[1]中的命题2.2,可得
(13)
结合(11)~(13)式和系统{f,φ,g,δC;ft:t∈T}在点(x0,y0)满足F-(BCQ)条件,可得
(u*+x*,y*)+N((x0,y0);C)+
注意到对于∀t∈T,有
∂ft(x0,y0)⊆∂xft(x0,y0)×∂yft(x0,y0),
N((x0,y0);C)⊆NX((x0,y0);C)×NY((x0,y0);C),
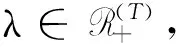
结合(5)式可知
故(8)式成立.证毕.
由定理1可得如下推论:
推论2设x0∈domM,y0是含参DC复合优化问题
min(f∘φ)(x0,y)-g(x0,y)
s.t.y∈F(x0)∩G(x0)
(14)
(15)
由定理1、命题1、推论2和引理1,可得以下结论:
推论3若系统{f,φ,δC;ft:t∈T}在点(x0,y0)∈gphM满足(CBCQ)条件,则对于∀γ>0,(8)式成立.

推论5设(x0,y0)∈gphM∩φ-1(domf)∩intA.若函数f在φ(x0,y0)处连续,系统{δC;ft:t∈T}在点(x0,y0)满足(BCQ)条件,且
则对于∀γ>0,(8)式成立.
注1令φ为单位算子,则(1)式可以转化为文献[7]中的值函数,即
此时,本研究中的F-(BCQ)条件转化为文献[7]中的F-(BCQ)条件,即
由此可知,定理1推广了文献[7]中的结论.

