高温作用后砂岩物理力学性质阈值温度的确定——基于机器学习算法*

龙沁圆，梅 钢，田 红，徐能雄

(1.中国地质大学(北京)工程技术学院，北京 100083；2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

高温后岩石的物理力学性质与温度的相关性研究一直是岩石力学领域的重要研究课题.高温后岩石的多项物理力学参数均发生不同程度上的改变.Wang等[1]通过对马鞍山花岗岩的研究发现其波速、变异系数、渗透率随温度变化存在阈值.吴晓东等[2]发现热处理过程中岩石波速、渗透率和孔隙度等物理性质的变化存在一个突变温度域.支乐鹏等[3]推断110 ℃左右为花岗岩一个阈值温度，在这个温度之前，温度对花岗岩产生负损伤，花岗岩强度增强；推断600～800 ℃为花岗岩另一个阈值温度，超过这个温度花岗岩的力学性能会发生显著变化.杨礼宁等[4]发现砂岩的峰值强度在400 ℃上下有明显变化.李学成等[5]发现砂岩的渗透率在100～280 ℃内呈现缓慢下降趋势，渗透率在阈值温度280 ℃后，可增大数倍到数10倍，最高增幅达46倍.熊健等[6]发现四川盆地下志留统龙马溪组富有机质页岩的加热过程中存在一个阈值温度，阈值温度范围在300～400 ℃，随着温度的增加，页岩样品纵横波时差降低，而纵横波衰减系数增大，页岩样品单轴抗压强度降低，弹性模量下降，泊松比变化规律不明显.其他文献[7-9]也表明，一些岩石存在阈值温度，阈值温度附近岩石的物理或力学特性会发生显著变化.众多学者对于岩石的物理力学参数的研究多数为温度与单一参数的关系，但是岩石的物理力学性质之间还存在着非线性关系.

田红等[10]对黏土岩、砂岩、闪长岩、花岗岩均进行了大量实验，提供了不同种类岩石较为全面的物理力学特性的数据，拓展了人们对高温作用后岩石物理力学特性的认识，为处理和解决许多工程所涉及的高温岩土问题提供了定性分析和定量计算基础.

基于田红等[10]所著的《高温作用后岩石物理力学特性》中第四章砂岩的物理力学实验数据，通过机器学习的方法，采用SVM和K-Means的方法来解决此类高维度、非线性、小样本的问题，提出二分类法确定阈值温度，找出高温后砂岩物理力学性质的阈值温度，并对这种方法的合理性和准确性进行验证.研究内容主要包括以下三点：(1)采用K-Means的方法，找出砂岩样本的阈值温度区间；(2)采用相关性分析的方法，对用二分类法确定阈值温度区间的合理性进行验证；(3)采用SVM的方法，对用二分类法确定阈值温度区间的准确性进行验证.

1 阈值温度区间确定的二分类法

1.1 阈值温度

岩石的阈值温度指的是在这个温度范围内岩石的物理力学特性会发生显著变化，即在阈值温度附近岩石密度、纵波波速和弹性模量等物理力学性质参数变化幅度最大.

本研究所寻找的阈值温度区间，是指阈值温度存在的区间.通常，限于物理实验的成本和实验数据的数量，阈值温度不能完全精确地被确定，而只能确定一个区间，在这个区间进一步进行实验，可以缩小区间范围，最终可以确定精确的阈值温度.

1.2 二分类法

砂岩的物理力学性质在阈值温度上下有显著区别.根据温度不同，采用二分类法将砂岩的物理力学性质分为两类，其温度区间的界限就是该砂岩的阈值温度区间.

1.3 基于K-Means的阈值温度区间确定方法

1.3.1K-Means简介K-Means算法[11]主要用来解决聚类问题，是一种典型的无监督机器学习算法.它可以发现K个不同的簇，每个簇的中心采用簇中所含值的均值计算而成，每一个簇通过其质心，即簇中所有点的中心来描述.其基本思想为：首先随机确定K个初始点作为质心，将数据集中的点分配到距离最近的质心所对应的簇，将质心移动到这个簇所有点的平均值处，重复上述过程，直到质心不再移动，最终就得到了数据集的K个中心点.

1.2.2 阈值温度区间的确定 在对实验数据进行分析前，并不确定该样本的阈值温度是否存在以及阈值温度的区间，即并不知道分类的方法，进而无法对得到的样本数据进行分类.而K-Means是一种有利于聚类的算法，非常适合在不知如何进行分类时可以辅助找到分类的方法.

文献[10]中表4-3和4-4中编号2-0-1至10-20-3的74组样本数据(除编号8-20-3)的物理化学指标，笔者把质量和体积的变化数据处理为质量变化率和体积变化率，不考虑高度和直径的相关数据，在Pycharm上编程，输出结果见表1.

表1 K-means聚类算法下温度二分类法输出结果

从表1可以看出，温度存在明显分界.“1”类与“0”类的分界对应编号为4-20-3和6-0-1的两组数据，温度分别为400 ℃和600 ℃，表明根据400～600 ℃这一温度区间把样本数据分为两类的效果较好，即该砂岩的物理力学性质在这个温度区间上下有显著区别，这说明该区域岩体确实存在阈值温度，且区间为400～600 ℃，使得同一区域的同一种岩石的物理力学特性在温度≤400 ℃和温度≥600 ℃会存在显著差异.上述过程就是采用二分类法确定砂岩阈值温度区间的主要思路.

2 阈值温度区间的合理性验证

2.1 阈值温度上下的物理力学单特征量研究

高温下会使得岩石的物理力学特征发生改变，砂岩在高温作用后，其主要物理特征如密度、波速、体积变化率、质量变化率等皆会发生不同程度的改变.其主要力学特征如峰值应力、峰值应变、弹性模量等也会发生不同程度的改变.表2和表3分别列出不同温度下砂岩岩样物理特征和力学性质数据平均值.

表2 不同温度下砂岩岩样物理特征数据平均值

表3 不同温度下砂岩岩样力学性质数据平均值

从表2～3可以看出：该砂岩在400～600 ℃上下的物理和力学性质有显著差异，在这个区间内岩石的物理力学特性变化幅度最大，400～600 ℃这个区间符合1.1节中对阈值温度区间的定义，即400～600 ℃确实为该砂岩的阈值温度区间.

如果把阈值温度作为对该砂岩分类的分界线，那么可以将砂岩成功分成两类.相反，如果可以把岩样的物理力学性质根据温度分成两类，那么其分界区间即为阈值温度区间.即根据二分类法确定阈值温度是合理且可行的.

2.2 样本在三维空间的物理力学性质主要特征量分布特征研究

由于密度是岩石物理性质的主要表现，波速和弹性模量可以代表岩石的主要化学特性，故选用这三个因素研究岩样在三维空间的分布特征，可以看出岩样的三个要素在三维空间具有明显分界，即可以根据阈值温度将岩样的物理力学性质数据分为两类，也可以通过对岩样的物理力学性质的二分类法确定岩石的阈值温度区间.

将实验的74组数据在三维空间中投点(图1).从正面图、俯视图、侧面图均可以看出两种温度的砂岩在三维空间中呈按区域分布的特点，且假设400～600 ℃中存在阈值温度成立，可见阈值温度以上的砂岩物理力学特性在空间上分布比较集中，而阈值温度以下的砂岩物理力学特性则较为分散.左上方的蓝色点为误差数据，根据上一章的研究也可验证是编号为6-15-2的岩样出现较大偏离，可能是实验误差的影响.

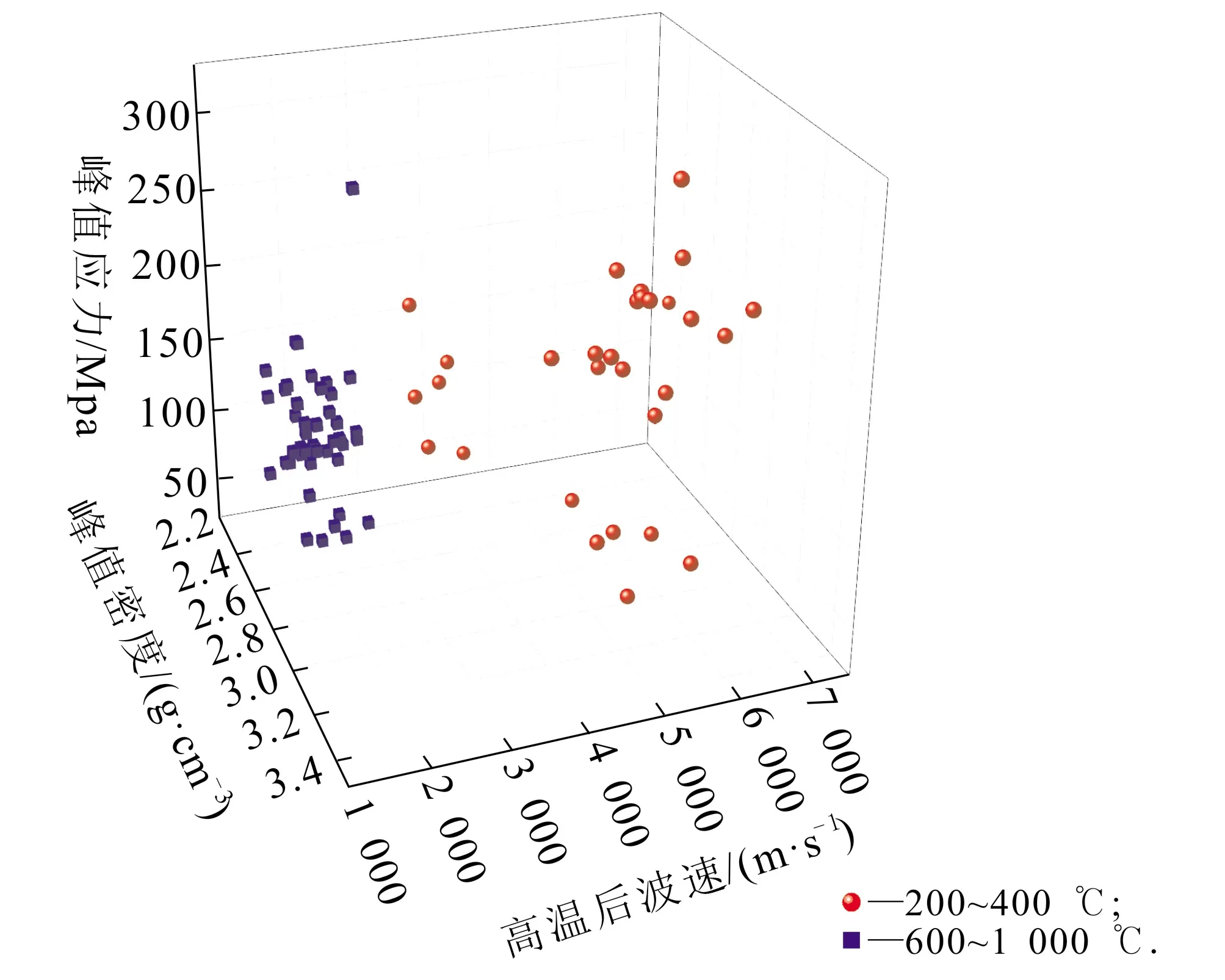
图1 样本在三维空间的物理力学性质主要特征量的分布特征

从散图1可以看出，左上角存在一个蓝色方体，即分类阈值温度以上的岩样数据分布到了分类阈值温度以下的空间区域，从表1也可以看出，第41位的岩样数据被分类为“1”类，而其周围的数据都为“0”类.深入研究发现，这一数据对应三维空间的点即为上述分布错误的左上角方体点，这个点对应的数据即为异常样本数据(表4).

表4 三维投影图异常样本数据整理

上述结果表明：

(1)该砂岩样本确实存在阈值温度且区间为400～600 ℃；

(2)阈值温度上下的砂岩物理力学特性具有可区分性.将实验所测数据的密度、波速、弹性模量这三个主要因素在空间投点，阈值温度上下的砂岩三要素在空间中是按区域分布的.

(3)阈值温度区间以下的样本物理力学特性分布比较分散，阈值温度区间以上的样本物理力学特性分布比较集中；

(4)砂岩在阈值温度上下的物理力学性质有显著差异，即如果把阈值温度作为对该砂岩分类的分界线，可以将砂岩成功分成两类.相反，如果可以把岩样的物理力学性质根据温度分成两类，那么其分界区间即为阈值温度.即根据二分类法确定阈值温度是合理且可行的.

3 阈值温度区间的准确性验证

3.1 SVM简介

支持向量机理论(Support Vector Machine，SVM)是一种十分有效的分类算法，其以统计学习理论为基础，以追求结果风险最小化为目的，有利于小样本、高维度的数据分析[11].在解决线性可分问题时，SVM算法采用大间距分类法，找到一个分隔超平面，将数据正确分类，并使样本点距离超平面的间隔最大；在解决线性不可分问题时，引入松弛系数和惩罚系数来解决噪声数据；在解决非线性问题时，通过一个非线性映射，把样本空间映射到一个高维甚至无穷维的特征空间中，使得在原来样本空间中的非线性可分问题转化为特征空间中的线性可分问题，为了避免高维空间中复杂的点积运算，SVM采用核函数来构建最优决策函数.

3.2 基于SVM算法的二分类法准确性验证

基于文献[10]中表4-3和4-4中编号2-0-1到编号10-20-3的74组样本(除编号8-20-3)的物理化学指标的实验数据，笔者把温度为200～400 ℃的数据标为一类，温度为600～1 000 ℃的数据标为二类，在Pycharm上编程.

运行编写的SVM程序，输出结果为0.987 5，即根据阈值温度区间将该砂岩进行二分类的分类准确率为98.75%，可见此方法具有很高的准确性，那么将岩样进行二分类法从而确定阈值温度是可靠且准确的.在样本数据中去除异常样本数据后，再次运行编写的SVM程序，得到的分类准确率为100%.

如果采用SVM算法，仅对阈值温度区间上下的岩样物理特性进行二分类研究，改写相关代码，那么得出分类准确率为100%，可见该砂岩的物理特性在阈值温度上下有显著区别.如果仅对阈值温度区间上下的力学特性进行二分类研究，那么得出分类准确率为96.25%，可见该砂岩力学特性在阈值温度上下亦存在明显区别，但程度低于物理特性.

3.3 基于SVM算法的其他分类法准确性比较

3.3.1 温度全分类法 将样本按照温度五类200，400，600，800，1 000 ℃分类，即按照样本本身的实际温度进行全分类，其分类准确率仅为53.75%，即每个温度作用后的砂岩物理力学特性不具有显著差异，说明此分类方法不适用于该砂岩.

3.3.2 温度三分类法 将K-means算法程序进行局部改写，可以将样本按照温度≤400 ℃，400～600 ℃，≥600 ℃分为3类，结果见表5.

表5 SVM算法下温度三分类法结果

从表9可以看出，温度三分类法结果比较无序，说明此法不适用该砂岩，也说明该砂岩在实验的温度范围内不存在两个阈值温度.通过SVM算法验证温度四分类法，发现其与三分类法类似，均不适用于该砂岩分类.

3.3.3 其他二分类法 使用200～400 ℃，600～800 ℃，800～1 000 ℃三种区间将样本进行二分类，分类结果见表6.

表6 SVM算法下温度其他二分类法结果

由表6可知，三种二分类法的准确率均低于基于400～600 ℃阈值区间的二分类法，说明用阈值温度将岩体进行二分类的准确性最高，反证了前述温度区间均不是该砂岩的阈值温度，因此若能找到二分类准确率最高的分类方法，其所采用的分类区间即为岩样的阈值温度，再次验证了利用二分类法确定岩样的阈值温度是可行的.

4 结论

通过采用机器学习的方法，针对高温作用后某砂岩样本的物理力学实验数据，提出可以用于确定该砂岩物理力学性质阈值温度区间的二分类法，并通过K-Means、SVM算法验证该二分类法的合理性和准确性.主要结论如下：

(1)基于K-Means算法的聚类结果表明，该砂岩存在阈值温度，区间为400～600 ℃.

(2)基于相关性分析的方法，验证了采用二分类法确定砂岩阈值温度区间的合理性；同时发现，阈值温度上下砂岩的物理力学性质存在显著差异，体现为阈值温度区间以下的岩石物理力学性质较为分散，而阈值温度区间以上的岩石物理力学性质较为集中.

(3)采用SVM算法进行准确性验算，结果表明，含异常数据时二分类法准确率为98.75%，去除异常数据后准确率可达100%，说明采用二分类法确定砂岩阈值温度区间的准确性高.

值得注意的是，本研究的样本数据仅74组，且本研究对温度的分类局限于200，400，600，800，1 000 ℃，虽然可以确定阈值温度在400～600 ℃区间内，但是无法得到完全准确的阈值温度.后续研究工作中可以进行更多实验，以进一步缩小阈值温度区间范围最终确定精确的阈值温度.