分形集上的加权Iyengar型不等式

时统业, 董芳芳

(海军指挥学院, 江苏 南京 211800)

1 预备知识

设 f(x)是[a,b]上的凸函数, 则有

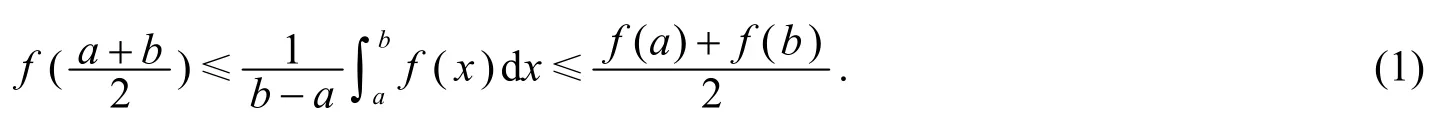
式(1)称为Hermite-Hadamard 不等式[1].

文[2]将式(1)加权推广为

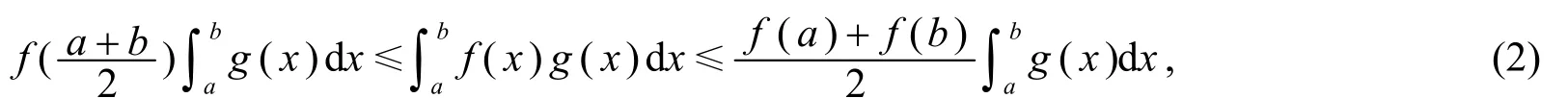
其中 f(x) 是[a,b]上的凸函数, g(x)是[a,b]上正的可积函数, 并且 g(x)关于对称.式(2)称为Hermite-Hadamard-Fejér 不等式.

定理1[3](Iyengar 不等式) 设f是[a,b]上的可微函数, 且存在常数M,使得对任意x∈[a,b]有|f′(x)|≤M, 则

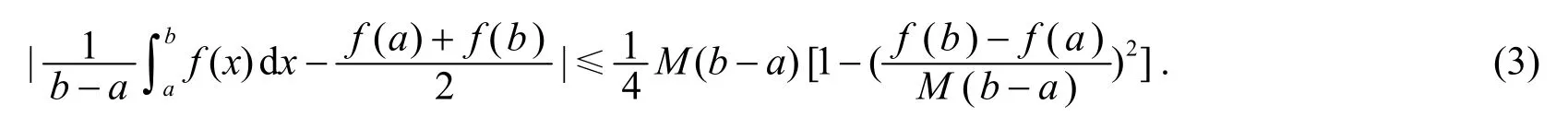
文[4]将式(3)推广为式(4).

定理2[4]设f(x)在[a,b]上可导,f′(x)在[a,b]上可积, 且在[a,b]上满足γ≤f′(x)≤Γ, 则有

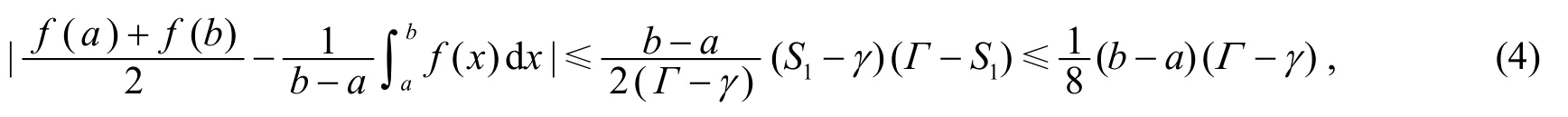
其中S1=

定理3[5]设f(x)在[a,b]上可导,f′ (x)在[a,b]上可积, 且满足γ≤f′(x)≤Γ,g(x)是[a,b]上正的可积函数, 且g(x)关于对称, 则有

近年来, 分形理论在科学工程领域有非常广泛的应用.文[6, 7]系统阐述了建立在分形空间上的局部分数阶微积分的相关理论.设 ℝα(0＜α≤1)是分形实线的α型集合,aα,bα,cα∈ℝα, 则在这个分形集中有如下运算律:

1)aα+bα∈ℝα,aα bα∈ℝα;

2)aα+bα=bα+aα=(a+b)α=(b+a)α;

3)aα+ (bα+cα)=(aα+bα)+cα;

4)aα bα=bα aα=(ab)α=(ba)α;

5)aα(bα cα)=(aα bα)cα;

6)aα(bα+cα)=aα bα+aα cα;

7)aα+ 0α=0α+aα=aα,aα1α=1α aα=aα.

下面使用Gao-Yang-Kang 的方法来描述局部分数阶的导数和积分.

定义1[6,7]设f:ℝ →ℝα是不可微函数, 如果对任意ε＞ 0, 存在δ＞ 0, 使得当|x-x0|＜δ时, 有|f(x) -f(x0)|＜εα, 则称f在点x0处局部分数阶连续.若f在区间I⊆ℝ 上局部分数阶连续, 则记为f∈Cα(I).

定义2[6,7]设f∈Cα(a,b), 则f在点x0处的局部分数阶导数定义为

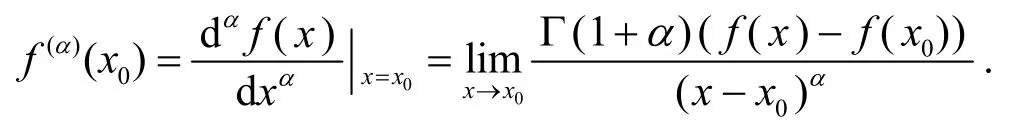
若对任意x∈I⊆ℝ 时存在f(α)(x), 则记为f∈Dα(I).

定义3[6]设f∈Cα[a,b],f在点[a,b]上的α阶局部分数阶积分定义为

其中a=t0＜t1＜…＜tN-1＜tN=b, Δtj=tj+1-t j(j=0,1,…,N-1), Δt=max{ Δt1, Δt2,…, ΔtN-1}.

规定当a=b时,当a＞b时,若对任意x∈[a,b]存在则记为

在闭区间上局部分数阶连续的函数是局部分数阶可积的.局部分数阶定积分有与黎曼定积分类似的性质, 如线性性质、区间可加性、比较性质、绝对不等式、牛顿-莱布尼茨公式、换元法、分部积分法等[6～8].

引理1[6](1) 设则特别地, 若f(x)恒为常数c, 则有

(2) 设f,g∈Dα[a,b]且f(α)(x),g(α)(x)∈Cα[a,b], 则

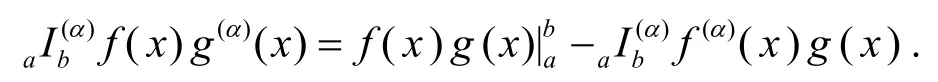
引理2[8]设f∈Cα[a,b], 0＜α≤1, 积分上限函数定义为则Π∈Dα[a,b], 且对于任意x∈[a,b]有Π(α)(x)=f(x).

引理3[9](局部分数阶微分中值定理) 设函数F(x)在[a,b]上连续, 在(a,b)上α阶局部分数阶可微, 则对于任意x0,x∈[a,b],x0＜x, 存在ξ∈[x0,x], 使得

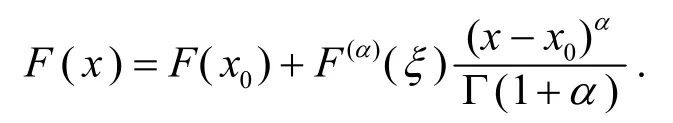
文[10]给出分形集上的广义凸函数的概念, 并建立了广义凸函数的Hermite-Hadamard 型不等式, 推广了凸函数的Hermite-Hadamard 型不等式.

定义4[10]设区间I⊆ℝ, 函数f:I→ℝα, 若对任意u,v∈I和任意λ∈[0,1], 有

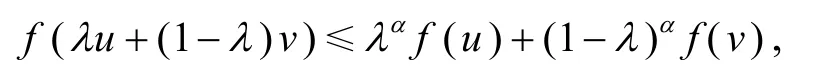
则称f是I上的广义凸函数.

定理4[10](广义凸函数的Hermite-Hadamard 型不等式) 设f:[a,b]→ℝα是[a,b]上的广义凸函数,则有

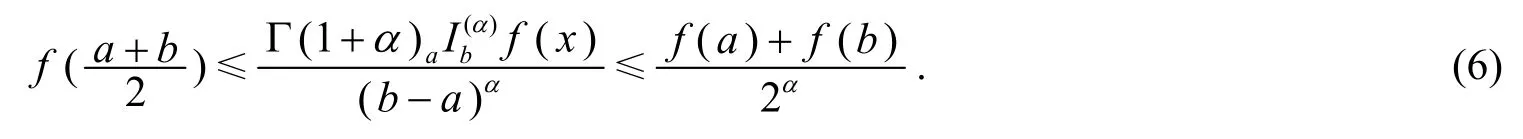
文[11]给出了式(6)的加权推广.

定理5[11](广义凸函数的Hermite-Hadamard-Fejér型不等式) 设是[a,b]上的广义凸函数,g:[a,b]→ℝα是非负的局部分数阶可积函数且关于对称, 则有

有关局部分数阶的不等式还可参阅文[12～15].本文仿照文[16]的方法, 将Iyengar 不等式(4)推广到分形集上.为证明本文的主要结论, 需要下面引理:

引理4[17]设f∈Dα[a,b],g∈Cα[a,b].若对任意x∈[a,b], 有则有

2 主要结果

定理6 设区间I⊆ℝ,I°是I的内部,f:I°→ℝα,a,b∈I°,a＜b,f∈Dα[a,b], 对任意x∈[a,b]有且存在常数γ,Γ∈ ℝα,γ＜Γ, 使得γ≤f(α)≤Γ,g∈Cα[a,b], 则对任意x∈[a,b]有

其中

证明对任意ε∈[a-x,b-x], 利用引理4, 有

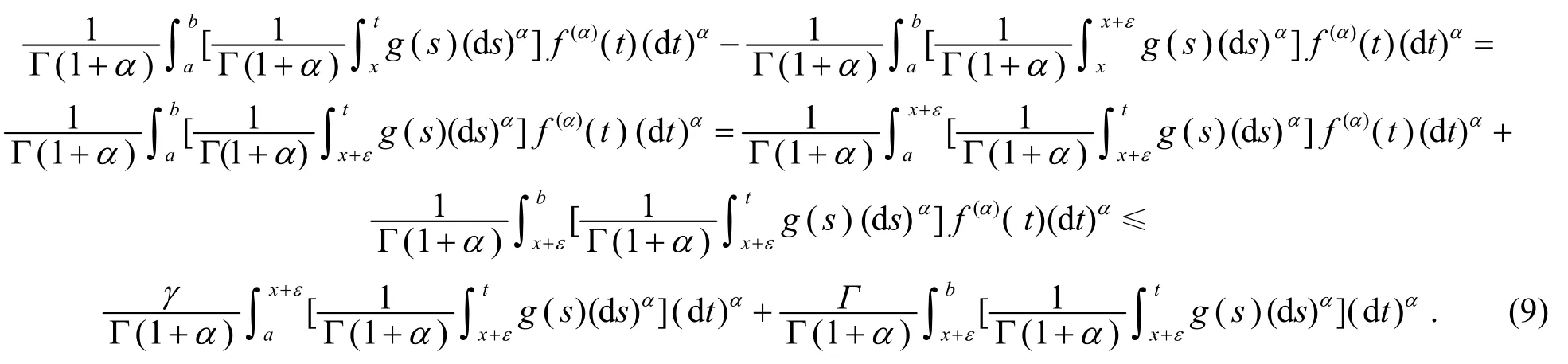
利用引理1 和引理2 得

类似得

综合式(9)～(11), 得

其中

于是有

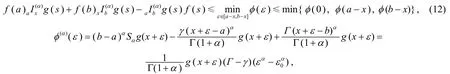
其中

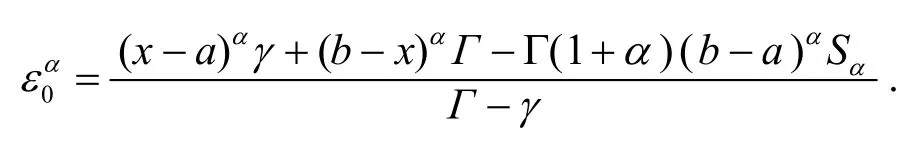
因为

而且由引理3 有γ≤Γ(1 +α)Sα≤Γ, 于是有从而有ε0∈[a-x,b-x].又因当a-x≤ε＜ε0时,当ε0＜ε≤b-x时,φ(α)(ε) ＞ 0, 故φ(ε)在点ε=ε0处取得最小值, 且

其中

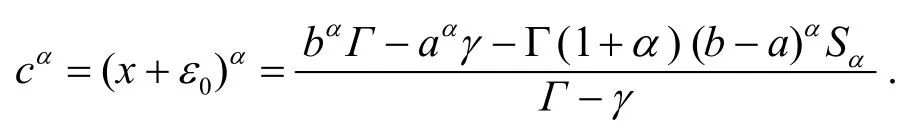
综合式(12)～(16), 则式(8)的右边两个不等式得证.

当γ≤f(α)≤Γ时, -Γ≤(-f)(α)≤-γ, 对-f应用上面结果, 则式(8)的左边两个不等式得证.

推论1 设区间I⊆ℝ,I°是I的内部,f:I°→ℝα,a,b∈I°,a＜b,f∈Dα[a,b], 对任意x∈[a,b]有且存在常数γ,Γ∈ ℝα,γ＜Γ, 使得γ≤f(α)≤Γ, 则对任意x∈[a,b]有

证明在定理6 中取 1g≡即可得证.

推论2 设区间I⊆ℝ,I°是I的内部,f:I°→ℝα,a,b∈I°,a＜b,f∈Dα[a,b], 对任意x∈[a,b]有且存在常数γ,Γ∈ ℝα,γ＜Γ, 使得γ≤f(α)≤Γ, 则有

证明在推论1 中取即可得证.

注1 式(17)给出了式(4)在分形空间上的推广.

推论3 设区间I⊆ℝ,I°是I的内部,f:I°→ℝα,a,b∈I°,a＜b,f∈Dα[a,b], 对任意x∈[a,b]有且存在常数γ,Γ∈ ℝα,γ＜Γ, 使得γ≤f(α)≤Γ,g∈Cα[a,b],g关于对称, 则有

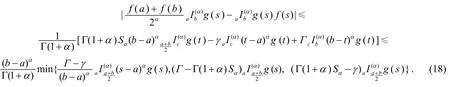
特别是, 当 1g≡时, 有

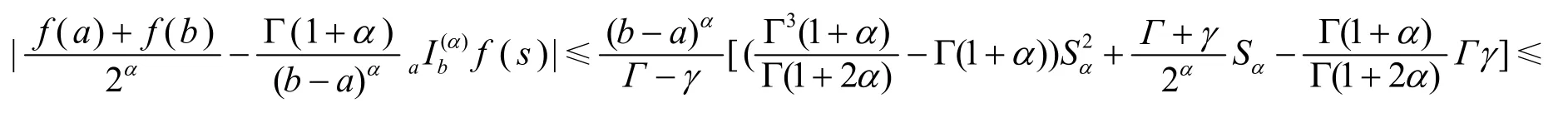
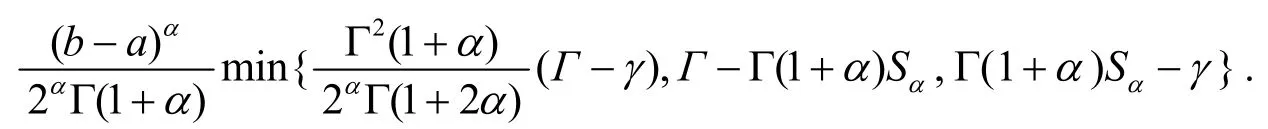
证明在定理6 中取则式(18)得证.

注2 式(18)给出了式(5)在分形空间上的推广.