利用Rüschendorf方法构造新的Copula

彭定忠, 何 帆, 刘朝才

(湖南理工学院 数学学院, 湖南 岳阳 414006)

0 引言

Copula 理论在分析变量间的相关结构时具有很多优点[1,2]: 首先, Copula 能对随机变量的边缘分布和相应的相关结构进行独立研究, 且边缘分布的选择不受限制; 其次, 由Copula 函数导出的一致性和相关性测度, 在严格单调递增的变换下不改变; 另外, Copula可用来构造灵活的多元分布.因此, Copula理论近年受到众多学者的关注, 并被广泛应用于各个领域, 例如, 金融保险[3,4]、地质统计学[5]和水文学[6～8]等.一大批构造Copula 的方法也被相继提出, 例如, 给定对角截面的Copula 的构造[9], 半线性Copula 的构造[10]和从单变量分布生成正弦Copula[11].特别地, Rüschendorf[12]发展了一种从2[0,1]内任意可积的二元函数出发构造具有均匀边缘分布的多元分布函数的方法.鉴于此, 本文主要研究通过选择适当的 f(x,y) 来构造新的Copula 函数.

1 预备知识

首先, 给出Copula 函数的定义.

定义1[1]若一个二元函数C:[0,1]2→[0,1]满足如下条件:

(Ⅰ) 对任意的变量t∈I=[0,1], 都有C(t,0)=C(0,t)=0,C(t,1)=C(1,t)=t;

(Ⅱ) 对任意的u1,u2,v1,v2∈I=[0,1], 且u1≤u2,v1≤v2, 有

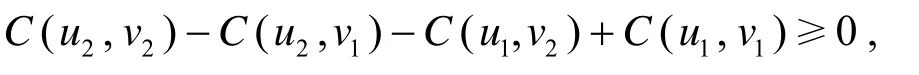
则称函数 C(u,v) 为Copula 函数.

条件(Ⅰ)称为二元函数具有有零基面(grounded); 条件(Ⅱ)称为二元函数二维递增.如果 C(u,v) 二阶可微, 那么条件(Ⅱ)等价于其中c(u,v)为C(u,v)的密度函数.

接下来介绍两种重要的由Copula 函数导出的相关性测度.

定义2[13]设X和Y是连续型随机变量, 它们具有Copula 函数 C(u,v), 则Kendall’sτ相关系数为

定义3[13]设X和Y是连续型随机变量, 它们具有Copula 函数 C(u,v), 则Spearman’sρ相关系数为

最后介绍Rüschendorf 方法.若 g(x,y) 满足

且1+g(x,y) ≥0, (x,y)∈I2, 则1+g(x,y)是某个C(u,v)的密度函数; 否则, 若g(x,y)在I2内有界, 记-a=inf[0,1]2{g(x,y)},b=sup[0,1]2{g(x,y)}, 则存在常数使 得 1+θg(x,y) ≥0, (x,y)∈I2, 此时1+θg(x,y)是某个C(u,v)的密度函数

满足式(3)和(4)的函数 g(x,y) 可按如下步骤求解:

第一步, 选择2[0,1]内任意可积的二元函数 f(x,y), 并计算

第二步, 令g(x,y)=f(x,y) -f1(x) -f2(y)+A.

2 主要结论

定理1 函数

是某个C(x,y)的密度函数, 其中

证明选取f(x,y)=6x2y, (x,y) ∈[0,1]2, 则

令

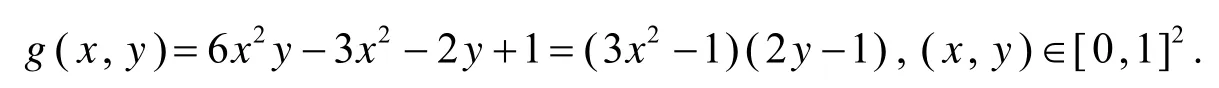
为了确定θ的取值范围, 需要求解 g(x,y) 的最值.由

解出 g(x,y) 的驻点为又

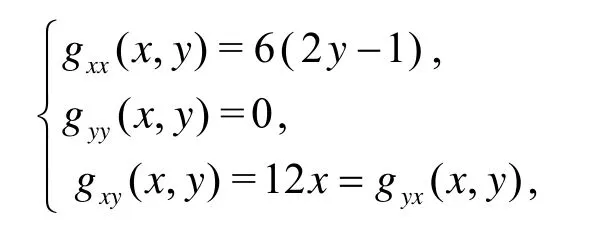
令

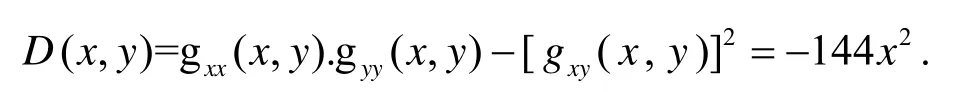
当x=0时,u1(y)=g(0,y)=1 - 2y且u1′ (y)=-2＜0, 故u1(0)=1为极大值,u1(1)=- 1为极小值;

当y=0时,v1(x)=g(x, 0)=1 - 3x2且v1′(x)=-6x, 故v1(0)=1为极大值,v1(1)=- 2为极小值;

当x=1时,u2(y)=g(1,y)=4y- 2且u2′(y)=4 ＞ 0, 故u2(0)=- 2为极小值,u2(1)=2为极大值;

当y=1时,v2(x)=g(x,1)=3x2- 1且v2′(x)=6x, 故v2(0)=-1 为极小值,v2(1)=2为极大值.

综上所述, 当 (x,y) ∈[0,1]2时, -2≤g(x,y)≤2, 则当时,

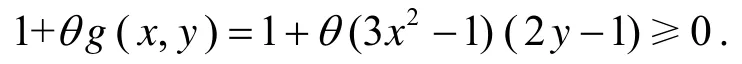
借助图1可更直观理解 c(x,y).

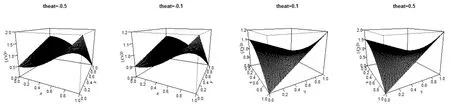
图1 c (x, y )三维视图

定理2 函数

证明由式(5)得

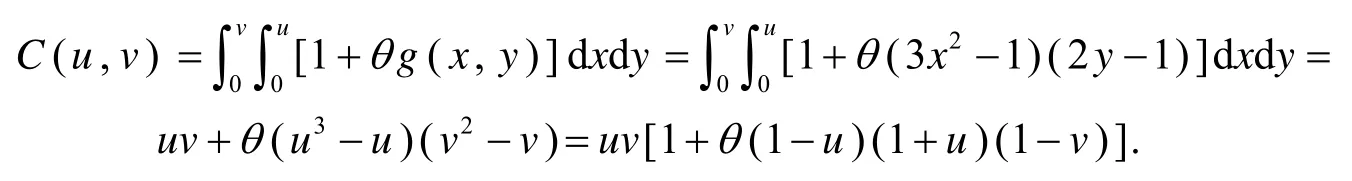
由定义1 知, 式(6)是一个Copula.

由图2可更直观理解 C(u,v), 其中实线对应 C(u,v), 虚线对应独立Copula.

图2 等值线图

注式(6)是对FGM-Copula[1](即C(u,v)=uv[1 +θ(1 -u)(1 -v)],θ∈[- 1,1])的一种推广, 同时也可看成文[14]的特殊情形.

定理3 设(X,Y) 具有式(6)所确定的Copula, 则

证明由式(6)得

将式(7)、(8)代入式(1), 得

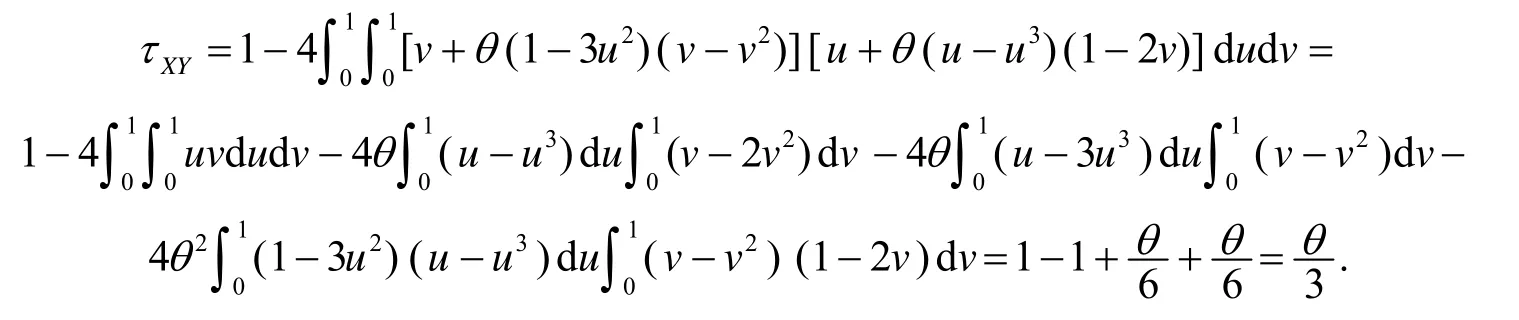
定理4 设(X,Y) 具有式(6)所确定的Copula, 则

证明将式(6)代入式(2), 得

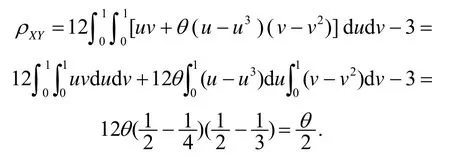
3 结束语

利用Rüschendorf 方法能从任意可积的二元函数出发构造新的Copula, 方法上具有很大的灵活性, 这为针对各种复杂的实际问题构建多元统计模型提供了一种可行方案.