具有B-D反应函数的交错扩散捕食模型中扩散的作用

柳文清，陈清婉

(闽南科技学院通识教育学院，福建 泉州 362300)

0 引 言

对于捕食-食饵模型，国内外已有许多研究，并且取得了许多有意义的成果.如解的整体存在性、稳定性、唯一性；解的局部和全局分歧及周期解等[1-4].在许多生态系统中，种群为获得赖以生存的食物和栖息环境，必然会向种群密度低的地方迁移，由于疾病的扩散、生物入侵等因素，也会导致种群不同程度的扩散.另外，种群之间的相互作用，例如种群之间的相互吸引、相互排斥，捕食者追逐猎物等也会导致种群扩散.基于以上背景，文献[5]首次提出如下具有交错扩散的种群竞争模型：

其中：d1、d2分别是u、v的扩散率；a11、a22是自扩散系数，表示种内生物竞争或避免拥挤所形成的扩散；a12>0、a21>0是交错扩散系数，表示竞争者种群之间相互作用形成的扩散.文献[6-15]进一步研究了两种群交错扩散捕食-食饵模型和互惠模型.但是带B-D功能性反应函数的交错扩散模型的研究很少见.本文考虑具有B-D功能性反应函数的交错扩散模型：

(1)

其中:u、v分别表示食饵和捕食者密度，边界条件表示系统是封闭的;r表示食饵内禀增长率;k表示环境容纳量;s为捕食者死亡率;p、q分别表示捕获率和食饵转化率;a、b表示捕食对食饵的饱和作用以及捕食者之间的相互作用.

本文的主要目的是研究系统(1)中交错扩散系数a21对系统的影响.为此，先分别讨论系统(1)的唯一正平衡点在a21=0时的局部稳定性和全局稳定性，证明了a21充分大时，正平衡点的不稳定性及交错扩散系数充分大时系统(1)非常数正平衡解的存在性.

通过简单计算，系统(1)存在唯一边界平衡点E1(k，0)，并且当满足条件

(H1)(q-sa)u*-s>0

时，存在唯一的非常数正平衡点E*(u*，v*)，其中：

1 交错扩散引起的Turing不稳定性

记Ω上的算子Δ在齐次Neuuman边界条件下的特征值序列为0=μ0≤μ1≤…≤μk≤…，U=(u，v)T，

于是系统(1)在平衡点E*(u*，v*)处的线性化问题为

Ut=ΦU(E*)ΔU+FU(E*)U.

对于i∈*，设λ是矩阵

-μiΦU(E*)+FU(E*)

(2)

的特征值，计算可得

由此得矩阵(2)的特征方程为

det[λI+μiΦU(E*)-FU(E*)]=λ2+Aiλ+Bi，i∈*，

(3)

通过计算可得

Ai=μiA11+μiA22-B11-B22，
Bi=(μiA11-B11) (μiA22-B22)- (μiA12-B12) (μiA21-B21),i∈*.

下面先证明a21=0时平衡点E*的局部稳定性和全局稳定性，再证明a21足够大时的不稳定性，以此说明交错扩散系数a21可引起Turing不稳定性.记

显然R2>1时，R1>1.

引理1当a21=0且R1>1时，系统(1)的平衡点是局部渐近稳定的.

证明：当R1>1时，有

从而Ai>0，Bi>0，此时特征方程的根均有负实部，故系统(1)当a21=0且R1>1时的平衡点是局部渐近稳定的.证毕.

定理1当a21=0且R2>1时，系统(1)的平衡点是全局渐近稳定的.

证明:构造Lyapunov函数

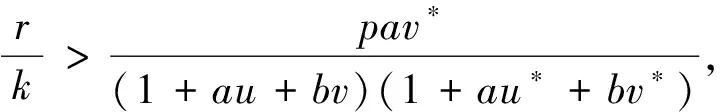
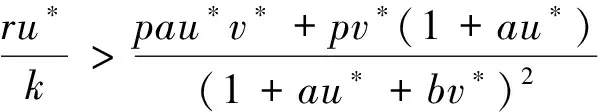
2 非常数正平衡解的存在性

考虑系统(1)所对应的椭圆方程组

(4)

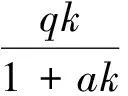
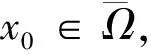
这表明

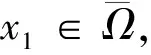
下面证明u，v的下界.因为φ1(x)满足方程

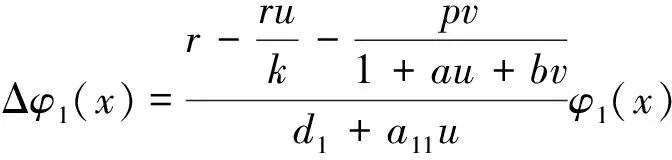
而且

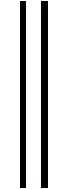
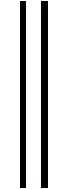
(5)

由于

再结合式(5)可得

(6)

同理存在正常数M5>0使得

(7)

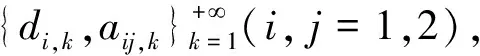
(8)

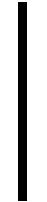
F(D，U)=U-(I-Δ)-1{[ΦU(U)]-1[F(U)+U·ΦUU(U)U]+U}=0，

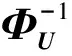
DUF(D，E*)=I-(I-Δ)-1{[ΦU(E*)]-1[FU(E*)+I]}.

记H(μi)=det{μiI-[ΦU(E*)]-1FU(E*)}(i∈*).由Leray-Schander定理，有以下引理:

引理3若对所有正整数i都有H(μi)≠0，则

由于det[ΦU(E*)]-1>0，故只需考虑det{μi[ΦU(E*)]-FU(E*)}的符号来判断H(μi)的符号.

定理3若

且存在某个奇数i∈*，有则存在正常数C*，当a21>C*时，系统(4)至少有一个非常数正平衡解.

证明:利用反证法.假设结论不成立.对t∈[0，1]，定义Φ(t，U)=((d1+a11u)u，(d2+a21u+a22v)v)T.考虑如下方程

(9)

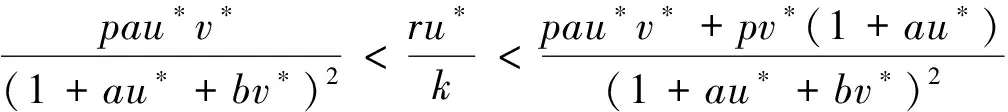
另一方面，当t=0时，由引理1的证明过程可知，当R1>1时，对所有μi≥0，H(μi)<0.故此时deg(F(D，·)，E*)=(-1)0=1.由Leray-Schander度的同伦不变性可得矛盾.这说明系统(4)至少有一个不同于E*的解.证毕.