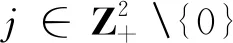带灾难的二维MX/M/1排队模型*

李俊平

(中南大学数学与统计学院,长沙，410083)

1 引言

排队模型是应用概率论的一个重要研究分支,在交通、通讯和服务性行业具有非常重要的应用. 排队模型的一般理论与连续时间 Markov链一般理论的相互结合已经成为一个非常成功和富有成果的研究领域. 在排队理论中, 成批到达和成批服务的排队模型在 Markov排队模型的理论和应用中具有重要的地位和作用. 由于其在许多领域中的广泛应用, 它吸引了众多概率论学者的关注和研究. 其中, 具有状态独立和状态依赖控制的 Markov排队模型也引起了许多学者的兴趣, 例如 Chen, Li, Hou 和 Wang[2], Chen, Pollett, Li 和 Zhang[3], Li, Zhang[12], 以及 Zhang, Li[15,16].

近来, 带有灾难的排队模型引起了许多学者的研究兴趣. 例如, Chen, Zhang, Liu 和 Rennolls[7], Di Crescenzo, Giorno, Nobile和Ricciardi[8], Economou, Fakinos[9]讨论了带灾难的连续时间马尔可夫链的瞬时分布等性质. Chen 和 Renshaw[5,6]分析了灾难对M/M/1及相关Markov排队模型的影响, Zhang 和 Li[16]把这些结果推广到了M/M/c排队模型. KrishnaKumar 和 Arivudainambi[10]讨论了灾难对初始顾客数为随机情形的 Markov 排队系统的影响. Di Crescenzo, Giorno, Nobile 和Ricciardi[8]研究了带灾难的一般的生灭过程有效灾难的首次发生时间.

在通常情况下, 当系统状态为0时就认为灾难发生了,并且系统将永远停留在状态 0, 即 0 为吸收态. 在本文中, 假定灾难发生后系统仍可以从 0 状态转移到其它正状态, 排除了灾难发生后 0 为吸收态的情况. 这种灾难称之为有效灾难, 即当系统状态不为 0 时发生的灾难. 因此, 本文不考虑系统状态为 0 时有灾难发生的情形.

本文考虑带灾难的二维MX/M/1 排队模型,给出其有效灾难首次发生时间的概率密度函数的Laplace变换的精确表达式，以及有效灾难首次发生时间的数学期望和方差及其渐近性质.

考虑一个二维排队网络系统，系统中有两个服务站点，其演变规律可直观描述如下：

(1)顾客独立地成批到达两个站点，每一批到达的顾客数是随机的，且批与批之间的到达时间间隔相互独立并服从相同的指数分布；

(2)服务规则为先到先服务，每一个顾客的服务时间相互独立且服从相同的指数分布；

(3)一个顾客接受完服务后，可以选择转移到另一个服务站点，也可以直接离开系统；

(4)外部有一个灾难流影响系统，灾难流的到达服从泊松分布，灾难一旦发生，系统中顾客立即清空.

为方便起见，我们采用如下记号：

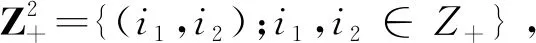
0=(0,0),e1=(1,0),e2=(0,1).

Q=Q*+Q(0)+Qc,

(1.1)

(1.2)

(1.3)

(1.4)

由于定义1.1中给出的Q是有界保守Q矩阵, 根据 Markov 链的一般理论, 存在唯一的过程, 即 Feller 最小过程, 满足 Kolmogorov 向前向后方程. 我们称这个过程为带灾难的二维MX/M/1 排队过程, 并记此过程为 {N(t);t≥0}.

特别地，若ξ=0， 即没有灾难，此时Q矩阵为

(1.5)

2 预备引理

为了研究带灾难的二维MX/M/1 排队模型, 我们引入如下发生函数:

显然,A(u),B(v)都在 [-1,1] 上有定义.

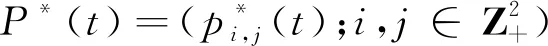
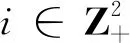
(2.2)

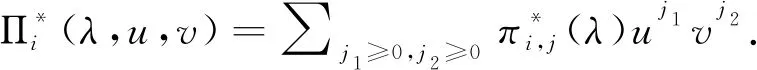
证明由 Kolmogorov 向前方程以及Q*的特殊性立得.

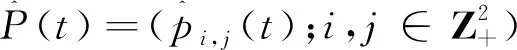
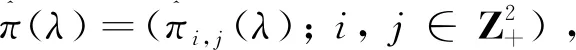
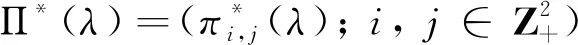
3 有效灾难首次发生时刻

本节我们来考虑过程 {N(t);t≥0} 有效灾难的首次发生时间.

(3.1)

初始条件为pj,n(0)=δj,n.

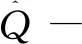
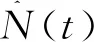
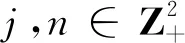
(3.2)

或者,

(3.3)

证明由于引理所涉及的Q矩阵都是有界保守的，只需证明(3.2)式定义的pj,n(t) 满足Q对应的Kolmogorov向前方程即可. 事实上，

这就证明了(3.2)式. 对(3.2)式作 Laplace 变换即可得到 (3.3)式. 证明完毕.

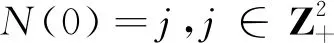
(3.4)

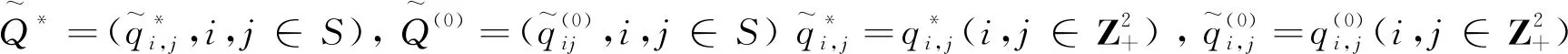
(3.5)

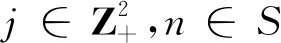
(3.6)

其初始条件为hj,n(0)=δj,n.由文献[8]知,{M(t);t≥0}和Cj,0之间有以下关系：

(3.7)

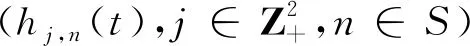
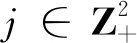
(3.8)

(3.9)

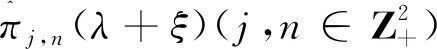
证明当j=0时, 对(3.6)后两个方程取Laplace变换, 得

(3.10)

同时，对(3.1)取Laplace变换,得

(3.11)

令

(3.12)

将(3.12)代入(3.10),并结合(3.11),可得

(3.13)

将(3.13)代入(3.12),并利用(3.3)式,可得当j=0时(3.9)成立.

一般地，当j≠0 时,

(3.14)

令

(3.15)

对(3.1)代入取Laplace变换,并把(3.15)代入(3.14),可得

(3.16)

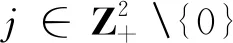
最后, 将 (3.6) 的第一个方程做 Laplace 变换, 得

因此, 由 (3.9) 立即得到 (3.8). 证明完毕.

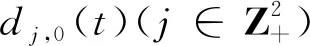
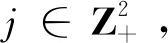
(3.17)

pj,n(t)=P(Nt=n|N0=j)

=P(Nt=n,Cj,0>t|N0=j)+P(Nt=n,Cj,0t|N0=j)

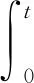
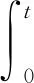
对上式取Laplace变换, 得

πj,n(λ)=ηj,n(λ)+Δj,n(λ)π0,n(λ),

接下来我们考虑有效灾难的首次发生时间Cj,0的期望和方差.

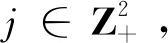
(3.18)

(3.19)

证明由于

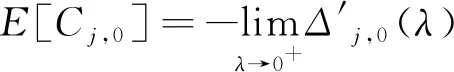
由 (3.17) 经过简单的代数运算即可得到 (3.18)和 (3.19). 证明完毕.

下面的定理给出了当ξ↓0 时平均有效灾难的首次发生时间E[Cj,0] 的渐近性质.

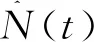
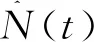
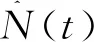
证明完毕.

最后，我们来考虑当ξ→+∞ 时平均有效灾难的首次发生时间E[Cj,0] 的渐近性质.

定理3.4我们有

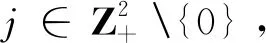
证明由于

由 (3.18) 得

利用Tauberian定理可得