具有区间时滞的中立型Luré系统的稳定性分析*

刘心歌 徐巧玲 唐美兰

(中南大学数学与统计学院,长沙,410083)

1 引言

Luré系统在液压控制、蔡氏电路、航空航天等相关的动力学系统领域中有着重要的应用,引起了国内外学者的广泛关注,同时对它们的研究也取得了丰富的成果.然而由于时滞的存在,导致Luré系统稳定性降低,进而引起相关性能下降.本文将考虑下列一类具有区间时变时滞的中立型Luré控制系统:

(1.1)

其中x(t)∈Rn,σ(t)∈Rm分别表示系统的状态和输出向量,矩阵A,A1,B,C和H是已知实矩阵,矩阵C的谱半径ρ(C)<1,φ(s)∈Rn表示在[-max{h2,τ},0]上的连续初始函数,连续可微的时滞函数h(t),τ(t)满足以下条件:

(1.2)

其中τ>0,τd<1,h,hd表示已知的常数,非线性函数f(σ(t))=[f1(σ1(t)),f2(σ2(t)),…,fm(σm(t))]T表示反馈输出向量,fi(σi(t))满足有限的扇形约束条件(其中ki为正数):

或者满足无限的开平面约束条件:

fi(σi(t))∈K[0,∞]∶={fi(σi(t))|fi(0)=0,σi(t)fi(σi(t))>0,σi(t)≠0}.

(1.4)

定义2.1([1]) 如果非线性函数f满足条件(1.3)或条件(1.4),且区间时变时滞中立型Luré系统在平衡点x(t)=0处渐近稳定,则称系统(1.1)是绝对稳定的.

本文利用Lyapunov-Krasovskii泛函(LKF)方法,建立含有区间时滞的中立型Luré时滞系统(1.1)的完全稳定性定理.

2 几个引理

引理2.1([2]) 设g1,g2,…,gN:Rm→R.若在Rm的开子集D上每个gi(t)>0,且满足

其中xij:Rm→R,xji(t)=xij(t),则有

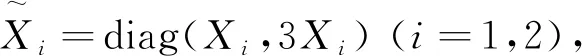
(2.1)

其中

引理2.3([4]) 设函数x:[a,b]→Rn连续,则对于任意正定矩阵R∈Rn×n,有下列不等式成立:

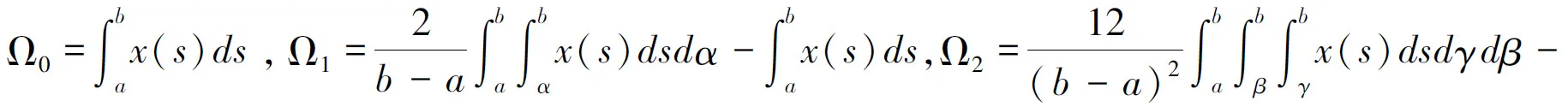
引理2.4([4]) 设函数x(s)在区间[a,b]上连续可微,则对于任意合适维数的正定矩阵R,有下列不等式成立:

其中

引理2.5([5]) 设函数x(s)在区间[a,b]上连续可微,则对任意正定矩阵R,有下列不等式成立：

其中

3 稳定性结论

为了方便分析具有区间时滞的中立型Luré控制系统的稳定性，我们引入以下记号

ei=[0n×(i-1)n,In,0n×(7-i)n,0n×m,0n×n]T,i=1,…,7，

e8=[0m×7n,Im,0m×3n]T,

ei=[0n×7n,0n×m,0n×(i-9)n,In,0n×(27-i)]T,i=9,…,27，

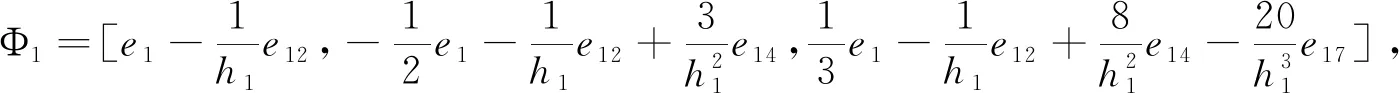
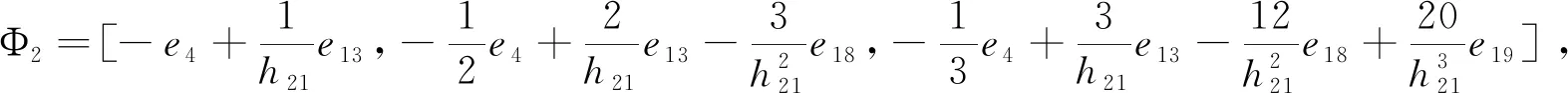
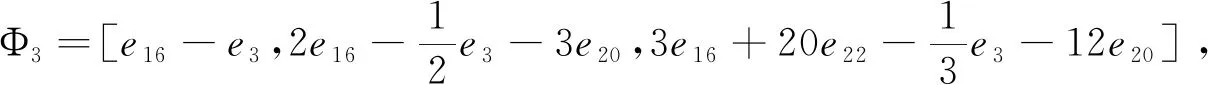
Φ5=[e3-e2,e3+e2-2e15,e3+6e15-e2-12e21],

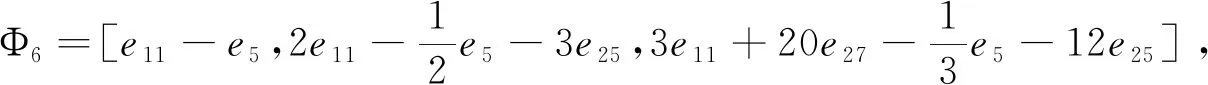
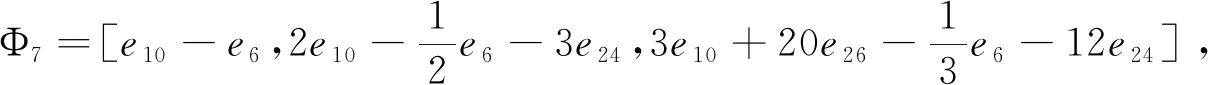
Φ8=[e6-e5,e5+e6-2e11,e6+6e11-e5-12e25],

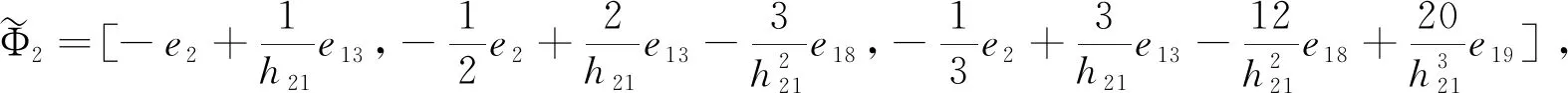
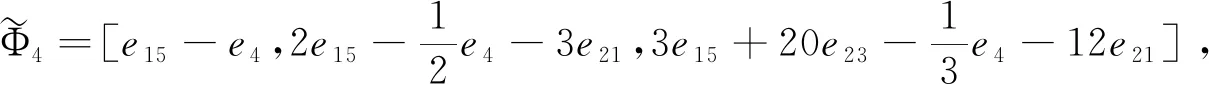
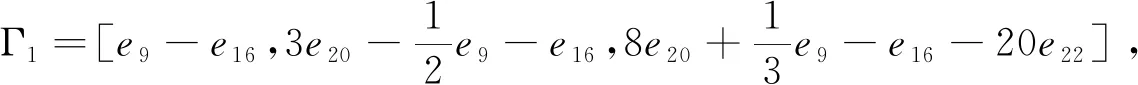
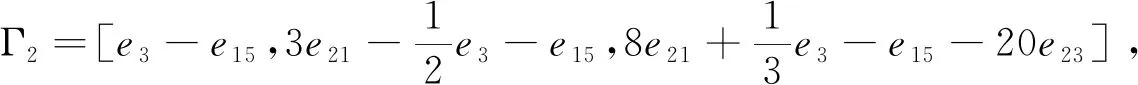
Γ3=[e9-e3,e9+e3-2e16,e9+6e16-e3-12e20],

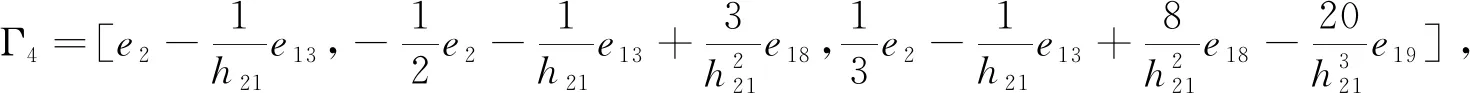
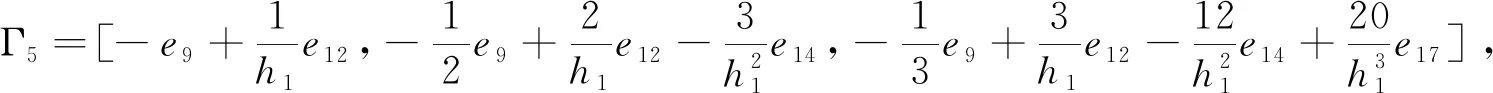
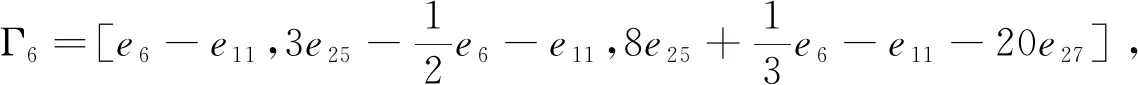
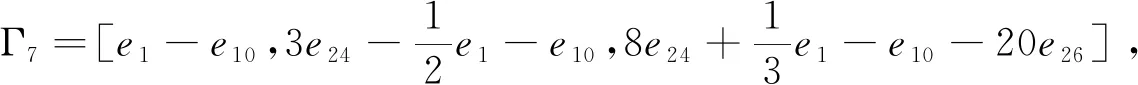
Γ8=[e1-e6,e1+e6-2e10,e1+6e10-e6-12e24],

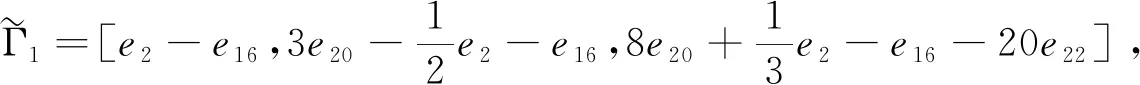
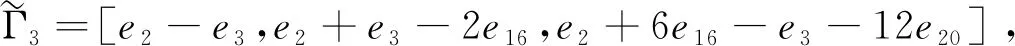
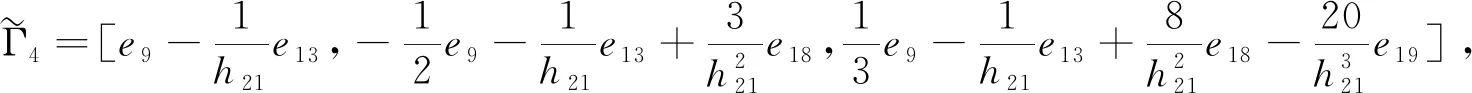
Π51=[e16,0,2e20-e16,0,12e22-6e20+e16,0],

Π52=[0,e9-e3,0,e9-2e16+e3,0,6e16+e9-e3-12e20],

Π61=[e15,0,2e21-e15,0,12e23-6e21+e15,0],

Π62=[0,e3-e2,0,e3-2e15+e2,0,6e15+e3-e2-12e21],

Π71=[e10,0,2e24-e10,0,12e26-6e24+e10,0],

Π72=[0,e1-e6,0,e1-2e10+e6,0,6e10+e1-e6-12e24],

Π81=[e11,0,2e25-e10,0,12e27-6e25+e10,0],

Π82=[0,e6-e5,0,e6-2e11+e5,0,6e11+e6-e5-12e25],

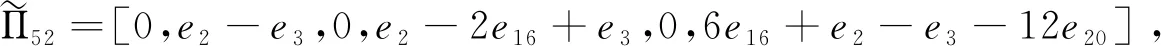
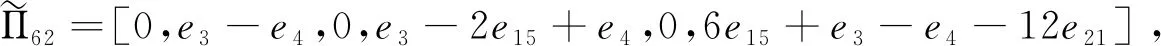
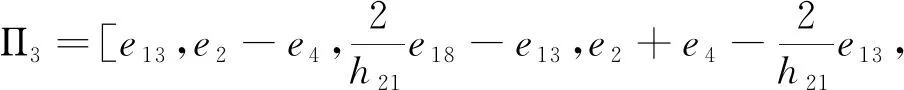
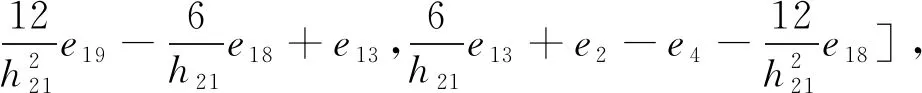
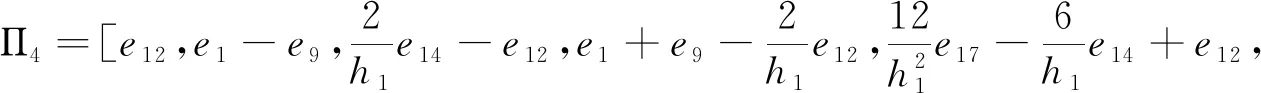
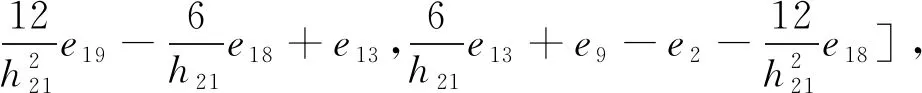
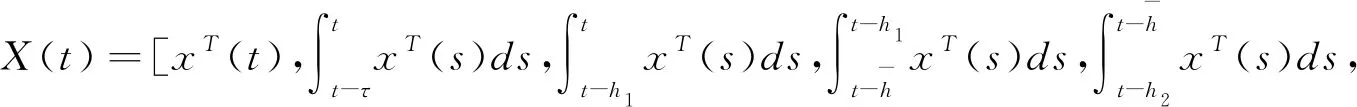
下面定理给出区间时滞中立型系统(1.1)的稳定性判据.

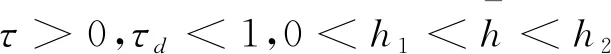
(3.1)

Ξ(h(t),τ(t))∶=Ξ1(h(t),τ(t))+Ξ2+Ξ3+Ξ4(h(t),τ(t))+Ξ5+Ξ6+Ξ7<0,

(3.2)

(3.3)

其中

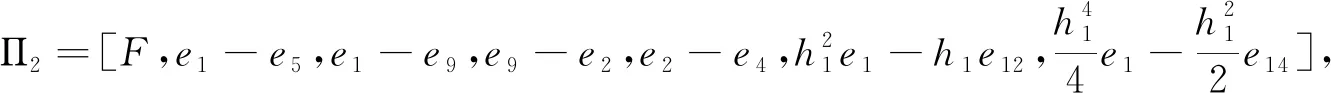
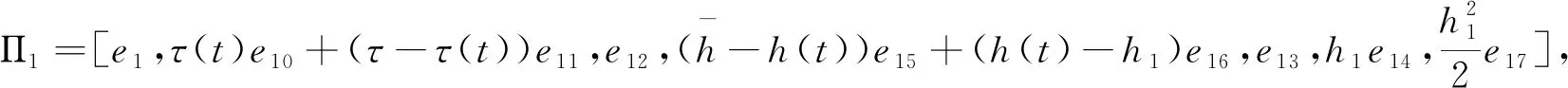
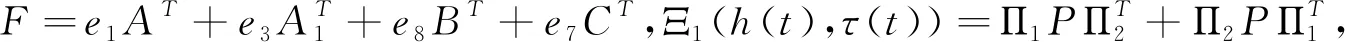
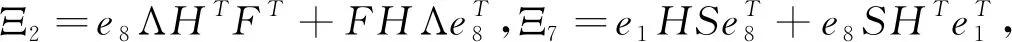
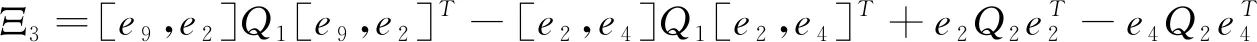
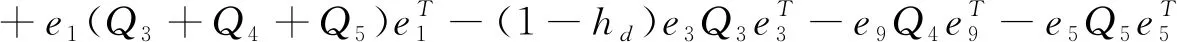
+[e1,F]Q6[e1,F]T-(1-τd)[e6,e7]Q6[e6,e7]T,

Ξ41(h(t))=Ψ1(h(t))-[Π52,Π62]M1[Π52,Π62]T,

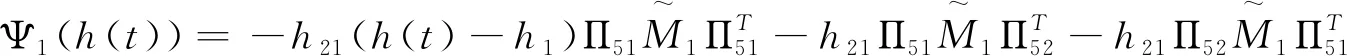
Ξ44(τ(t))=Ψ2(τ(t))-[Π72,Π82]M4[Π72,Π82]T,

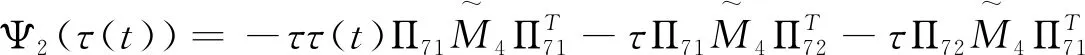
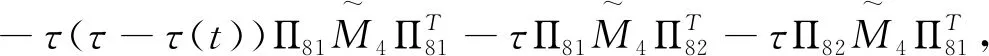
Ξ4(h(t),τ(t))=Ξ40+Ξ41(h(t))+Ξ42+Ξ44(τ(t)),

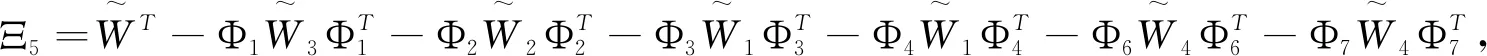
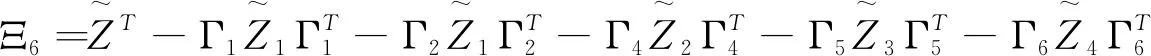
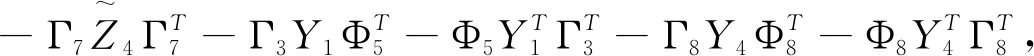
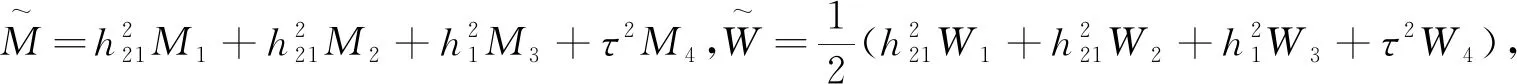
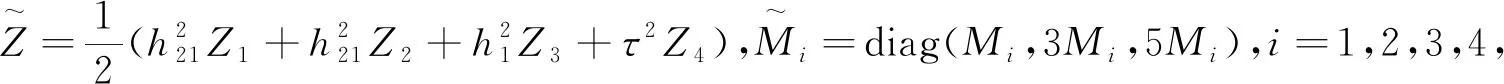
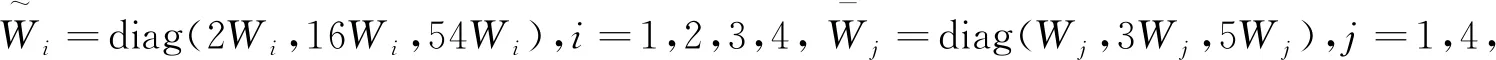
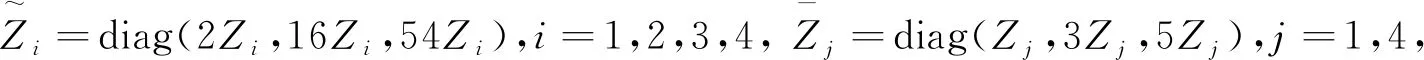
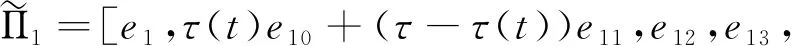
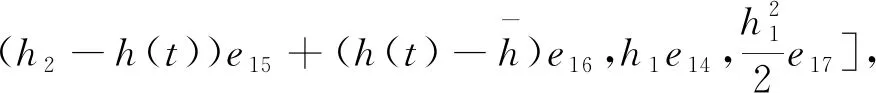
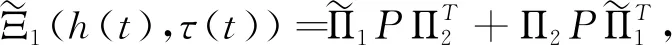
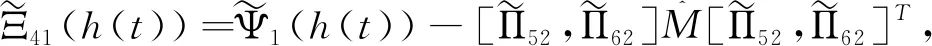
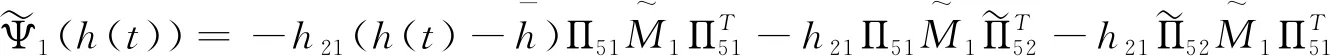
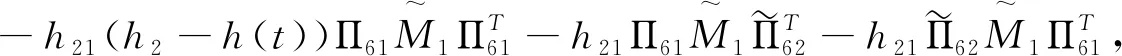
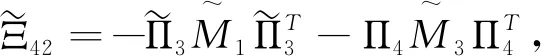
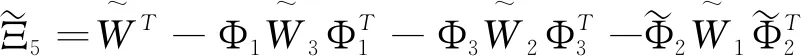
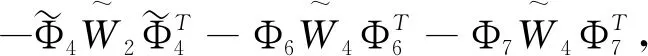
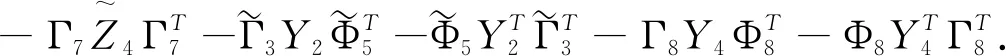
证明构造如下Lyapunov-Krasovskii泛函:

(3.4)

其中

V1(t)=XT(t)PX(t),

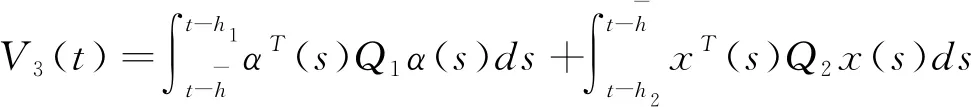
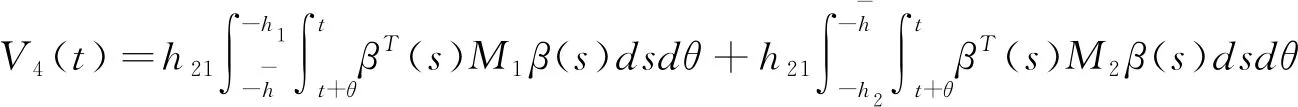
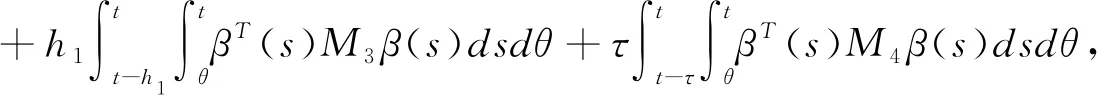
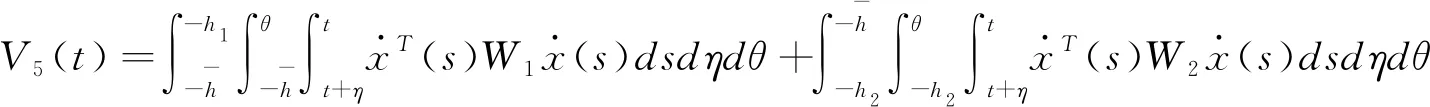
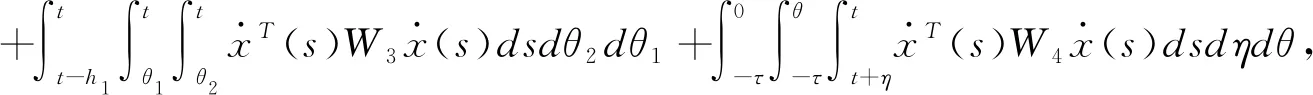
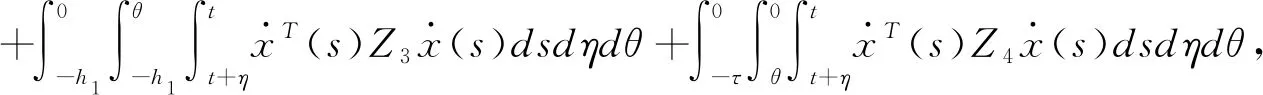
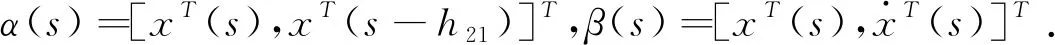
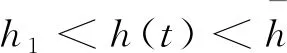
对于任意的t≥0,我们有

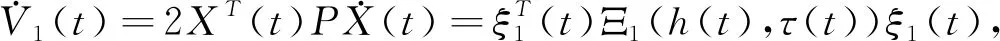
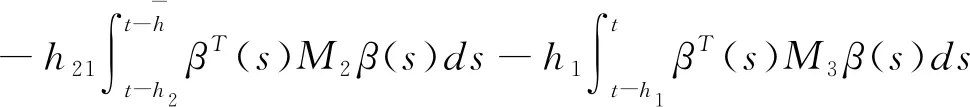
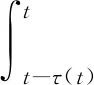
(3.5)

其中

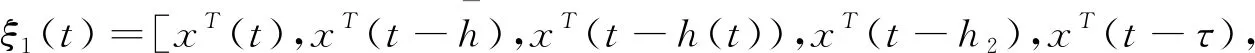
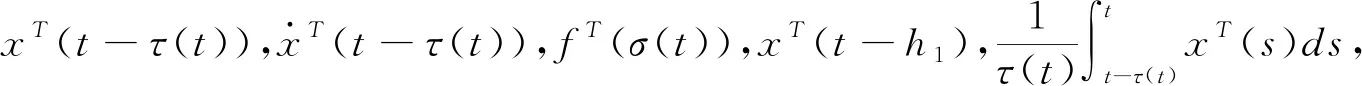
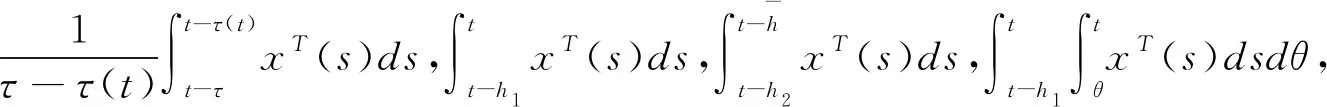
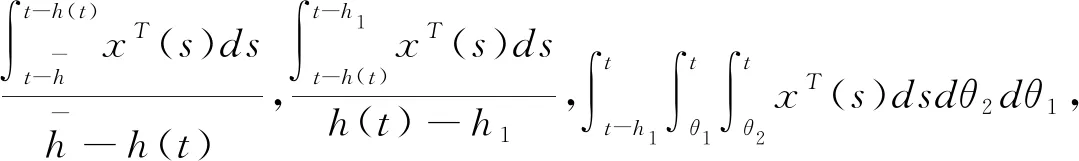
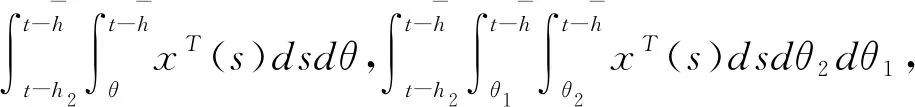
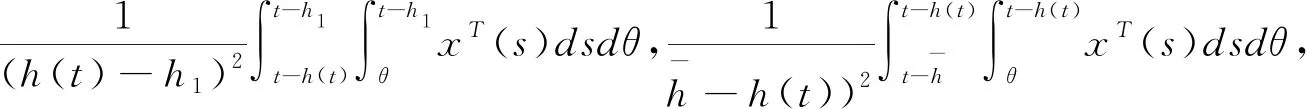
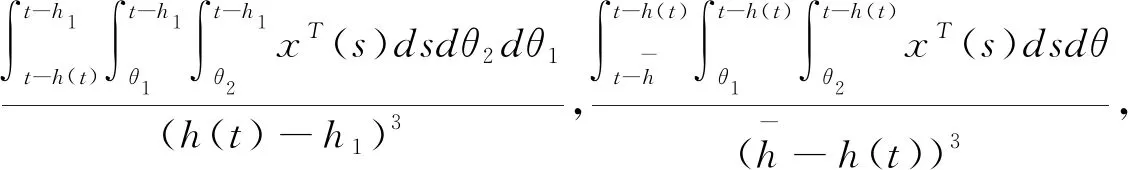
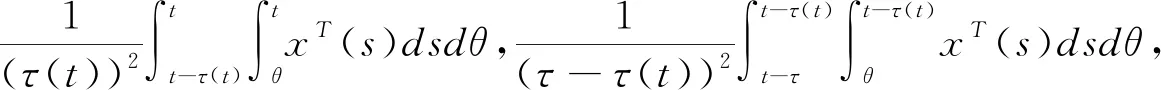
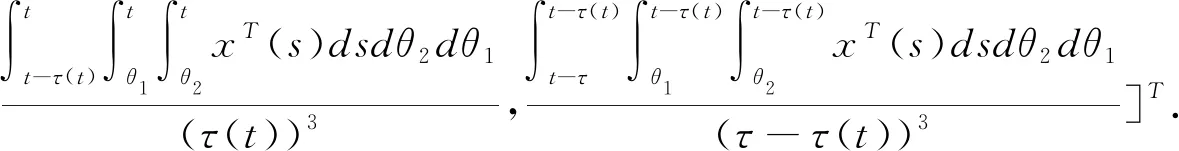
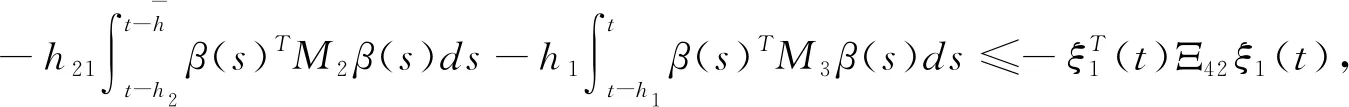
(3.6)

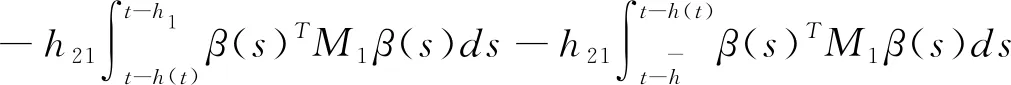
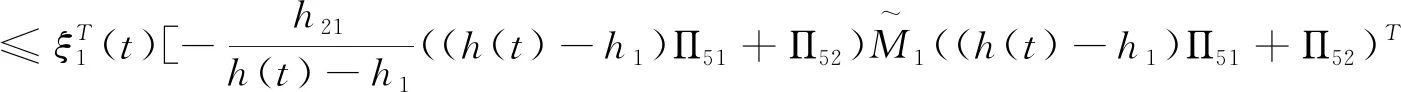
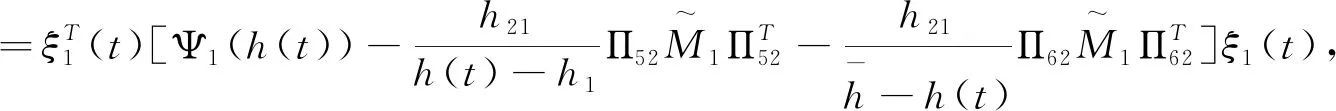
(3.7)

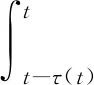
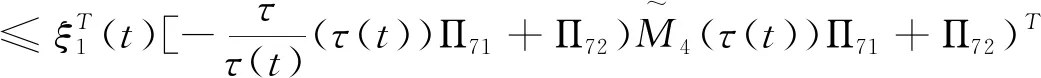
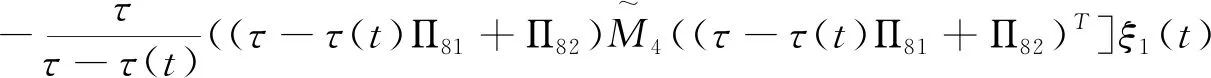
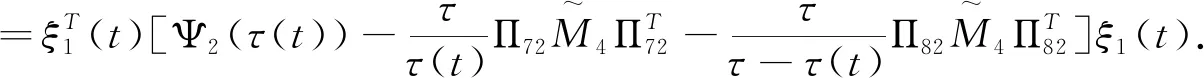
(3.8)

应用引理2.1,由(3.7)与(3.8)可得

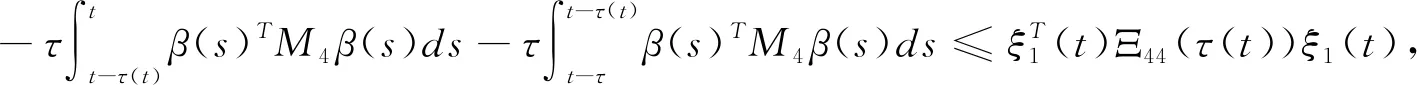
(3.9)

从而

(3.10)

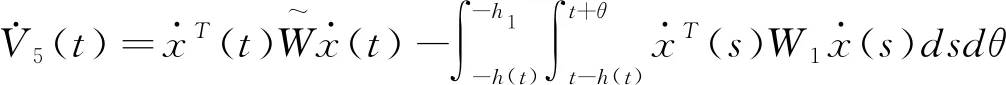
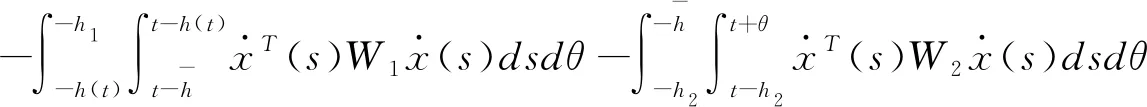
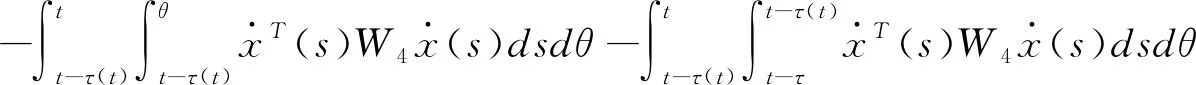
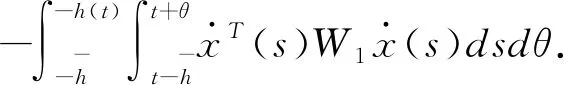
(3.11)

应用引理2.5中的第一个不等式可得

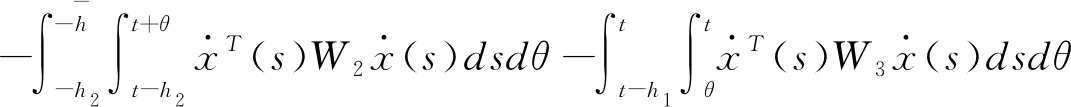
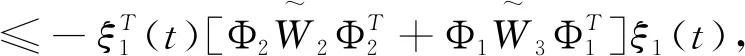
(3.12)

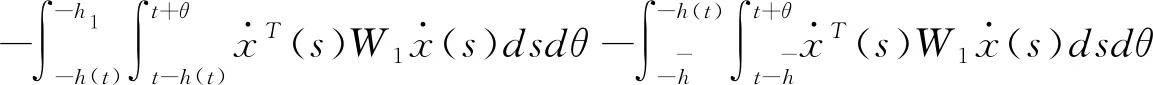
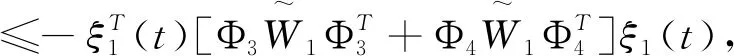
(3.13)

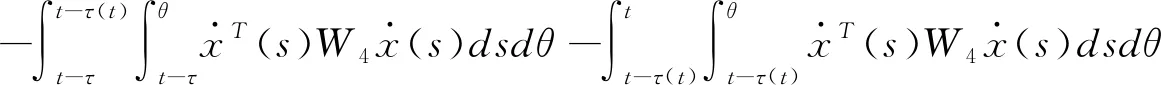
(3.14)

估计(3.11)中含W1和W4的二重积分,应用引理2.4可得

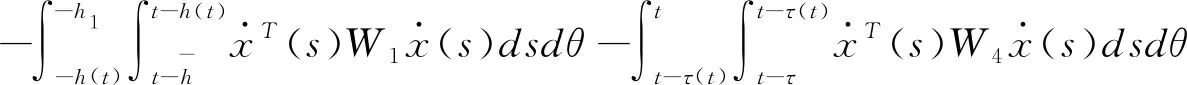
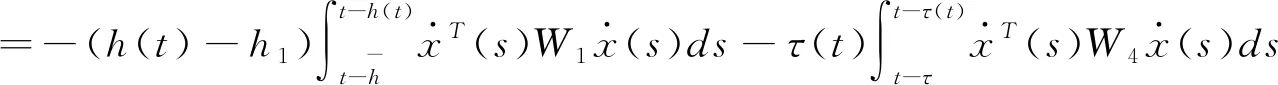
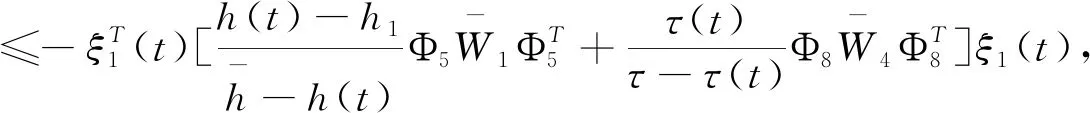
(3.15)

因此

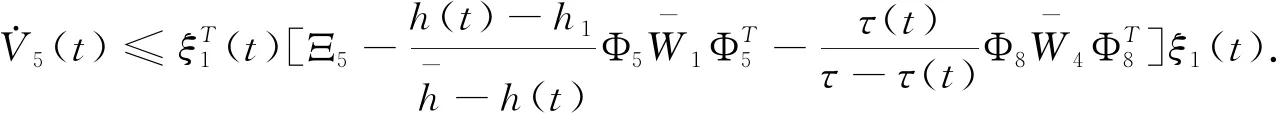
(3.16)

又

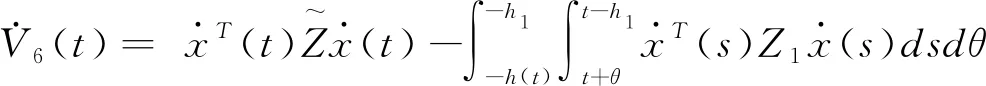
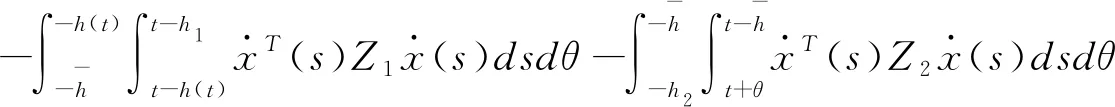
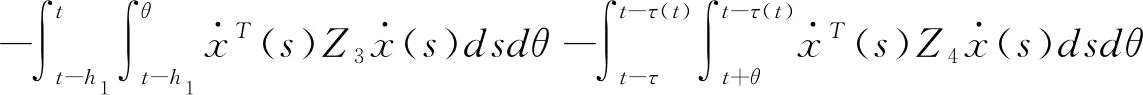
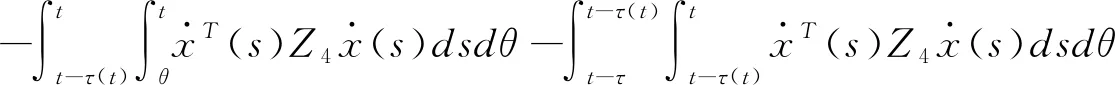
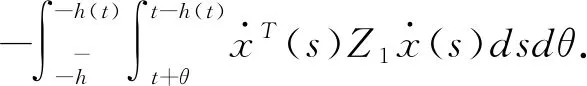
(3.17)

根据引理2.5可得

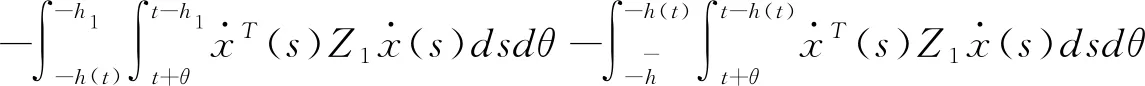
(3.18)

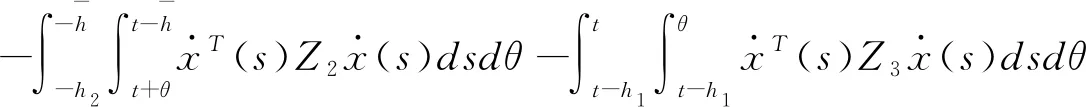
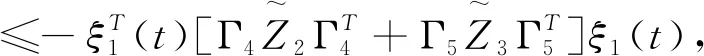
(3.19)

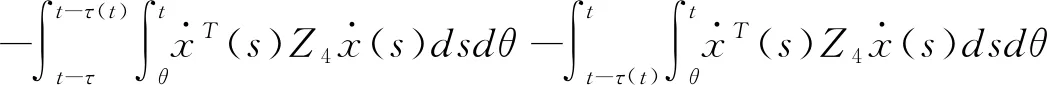
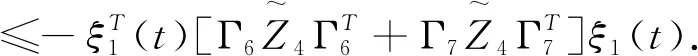
(3.20)

应用引理2.4有

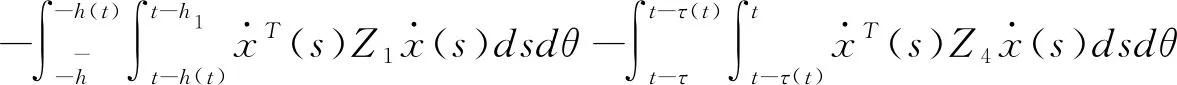
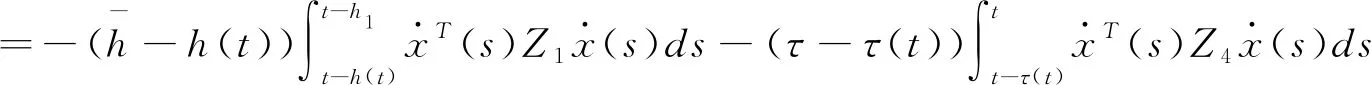
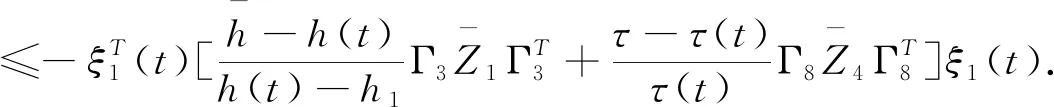
(3.21)

应用引理2.1,结合不等式(3.1)，(3.15)，(3.21)可得

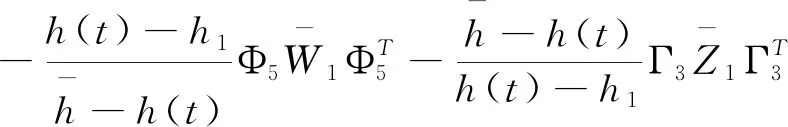
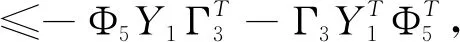
(3.22)

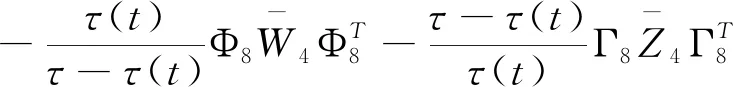
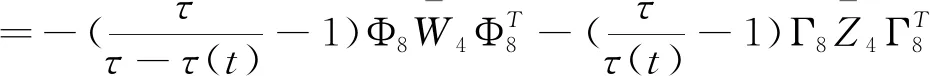
(3.23)

结合(3.16)-(3.23)可知

(3.24)

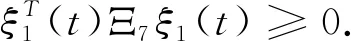
综上可得

(3.25)

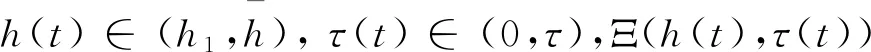
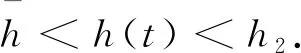
和情形一的处理方法类似,首先对V(t)求关于t的导函数.

(3.26)

(3.27)

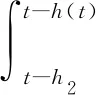
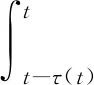
(3.28)

其中

(3.29)

应用引理2.3中的不等式可得

(3.30)

(3.31)

由引理2.1和(3.1)可知,

(3.32)

从而

(3.33)

(3.34)

根据引理2.5中第一个不等式有

(3.35)

(3.36)

再应用引理2.4可知

(3.37)

所以

(3.38)

又

(3.39)

由引理2.5中第二个不等式可得

(3.40)

(3.41)

根据引理2.2可知

(3.42)

再应用引理2.1中的倒凸公式得

(3.43)

综合上面(3.34)-(3.43),我们可以得到

(3.44)

从而

(3.45)

综上可知,当非线性扰动函数f(σ(t))满足条件(1.4)时,具有区间时变时滞的中立型Luré控制系统(1.1)是绝对稳定的.

4 数值算例

本节通过数值算例来说明我们获得的具有区间时滞中立型Luré系统绝对稳定性判断准则的可行性与优越性.

例4.1考虑下面的Luré中立型系统

σ(t)=HTx(t),∀t≥0,

(4.1)

其中

这个例子被广泛应用于中立型Luré时滞系统的绝对稳定性条件分析.从表1中我们可以看出,当τd=0.5,h1=0.5,τ=0.1时,对于不同的hd,按定理3.1计算所得使系统绝对稳定的可允许的最大时滞上界h2均大于文献[6,7,8]的结果.

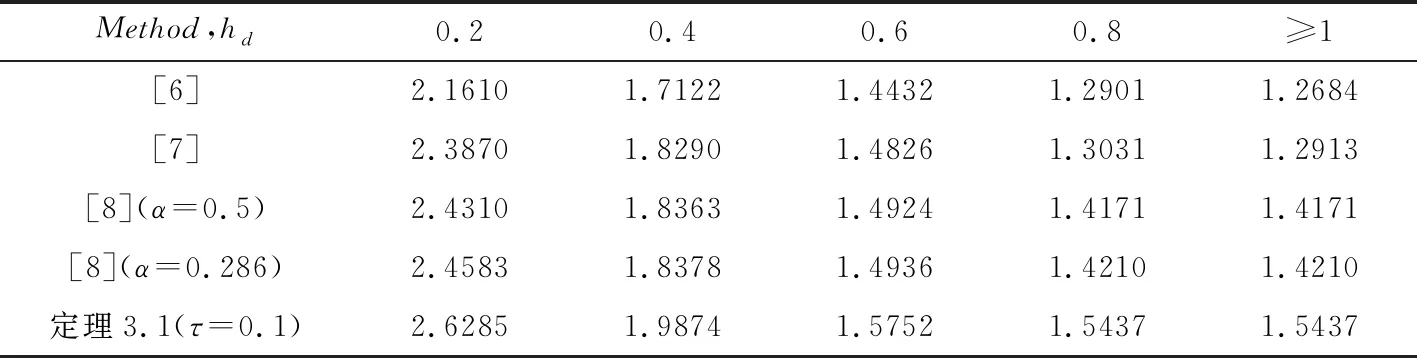
表1 可允许的最大时滞上界h2(h1=0.5,τd=0.5)