Existence and Axial Symmetry of Minimal Action Odd Solutions for 2-D Schrödinger-Newton Equation

Zhang Yang

(School of Mathematics and Statistics, Central South University, Changsha 410075, China)

Abstract We consider the following 2-D Schrödinger-Newton equation in R2 for all p≥2. Using variational method with the Cerami compactness property, we prove the existence of minimal action odd solutions. Also by carefully applying the method of moving plane to a similar but more complex equation on the upper half space, we prove these solutions are in fact axially symmetric. Our results can be seen partially as the counterpart of the results in [13] for the 2-D case, or the extension of the results in [10] to the odd solution case.

Key words Logarithmic convolution potential Cerami compactness Method of moving plane Schrödinger-Newton equation

1 Introduction and main results

In this paper, we study the following Schrödinger-Newton equation

(1.1)

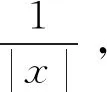
In the 2-D case, the analysis for this equation is harder, because of the sign-changing property of the log function, which is the fundamental solution ofΔinR2. First, Choquard, Stubby and Vuffray proved that there is a unique radial ground state solution by an ODE method forp=2, see [9]. Then Stubby established the variational framework and proved a stronger result by using the constraint minimization argument, see [28]. Based on this variational framework, Cingolani and Weth [10] discovered that the energy functional or aciton functional (p=2) satisfies the so-called Cerami compactness property, and used the minimax procedure to give the variational characterization of the ground state solution. They also showed the symmetry of these solutions and other properties. Additionally they proved the existence of infinitely many solutions of which the energies go to infinity and have many different types of symmetry in terms of groupG, see also [12]. Later Cao, Dai and Zhang extended these resuts to the general casep≥2 by using the same method, see [6]. For the sharp decay and non-degenerency, see [3].

In [13], the authors considered the existence of the minimal action odd solutions and minimal action nodal solutions inR3. From the results in [6,10] for the 2-D case, we know there indeed exist odd solutions and nodal solutions. So the odd solutions set and nodal solutions set are not empty. The natural questions for us are whether there exsits a minimal odd solution among all the odd solutions, and whether the minimal action odd solution is axially symmetry. We will give these two questions a firmative answer. Our results can be seen partially as the counterpart of [13] for the 2-D case, or can be seen as the extension of [6,10] to the odd solution case.

We consider the energy functional or the actional functional

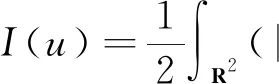
defined on the function space

where the Radon measure isdμ=log(1+|x|)dx. Formally, the Schrödinger-Newton equation is the corresponding Euler-Lagrange equation for this energy functional. The properties of the actional functional and function spaceXwill be given below, see also [6,10].

Now we define the odd function space

Xodd∶={u∈X|u(x1,-x2)=-u(x1,x2) for almost everyx=(x1,x2)∈R2}

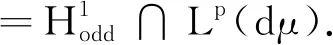
The norm onXoddis defined by

The odd Nehari manifold and the corresponding minimum is defined by

whereN={u∈X:〈I′(u),u〉=0,u≡0} is the Nehari manfold. Note thatNis not empty since we can always chooseuwith log|x-y||u|p(x)|u|p(y)dxdy<0 such that 〈I′(tu),tu〉=0 for somet>0. Also we define the odd ground state value by

cg,odd∶=inf {I(u):u≢0,u∈Xodd,I′(u)=0}.

We shall callcg,oddthe minimal action value, and the corresponding solutions the minimal action odd solutions, if they exist. The first minimax value is regularly defined on the function spaceXoddby

Also the mountain pass value is defined by

where Γ={γ∈C([0,1],Xodd):γ(0)=0,I∘γ(1)<0}.

Our first result is the existence of minimal action odd solutions.

Theorem 1.1Assumep≥2. Then we have:

1.cmp,odd>0;

2. there exists an odd solutionu∈Xodd{0}, such thatI(u)=cmp,odd;

3.cg,odd=codd=cmm,odd=cmp,odd;

4.cg,odd>cg, wherecgis the ground state energy inX.

Our second result is the axial symmetry for all the minimal action odd solutions.

The proof for this axial symmetry property is based on the method of moving plane. For this robust method, see [8,11,14,16,20,29].

2 Preliminaries

In this section, we list some preliminaries for proving the above two theorems, see the details in [10] forp=2 and in [6] forp≥2. We start from an elementary but very useful inequality, which is firstly used in proving the famous Brezis-Lieb lemma.

Lemma 2.1(ε-inequality) Let 00, there exists aCε>0 such that for alla,b∈C,

||a+b|p-|b|p|≤ε|b|p+Cε|a|p.

The proof can be seen in [18]. We will apply this simpleε-inequality in proving the strong convergence of Cerami sequence and the axial symmetry of minimal action odd solutions. We introduce the bilinear forms

B1(f,g)=∬log(1+|x-y|)f(x)g(y)dxdy,

B0(f,g)=B1(f,g)-B2(f,g)=∬log(|x-y|)f(x)g(y)dxdy

and the corresponding functionals

V1(u)=B1(|u|p,|u|p)=∬log(1+|x-y|)|u|p(x)|u|p(y)dxdy,

V0(u)=B0(|u|p,|u|p)=∬log(|x-y|)|u|p(x)|u|p(y)dxdy.

By the HLS inequality, we can boundV2(u) by

Using these notations, we can rewrite the action functional in a compact form

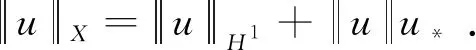
The next lemma gives some properties of the action functional and function space.

Lemma 2.2

1. The function spaceX=H1∩Lp(dμ) is compactly embedding inLs(R2) for alls∈[p,∞);

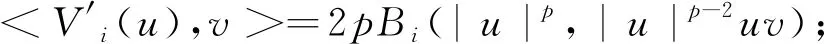
3.V1is weakly lower semicontiniuous onH1(R2);Iis weakly lower semecontiniuous onXand is lower semicontiniunous onH1.

The properties of the solutions are listed in the following lemma.

Lemma 2.3

1. Ifuis the critical point of the energy functional, thenuis the weak solution of the following Euler-Lagrange equation:

-Δu+u+(log|·|*|u|p)|u|p-2u=0;

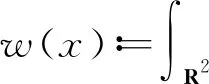
3.udecays exponentially: for any 0<ε<1, there is aCε>0 such that

|u(x)|≤Cεexp-(1-ε)|x|;

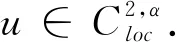
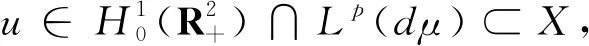
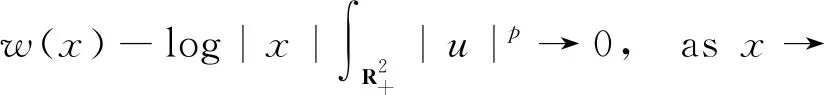
But by the odd symmetry, we have

Combining these two asymptotics, we have

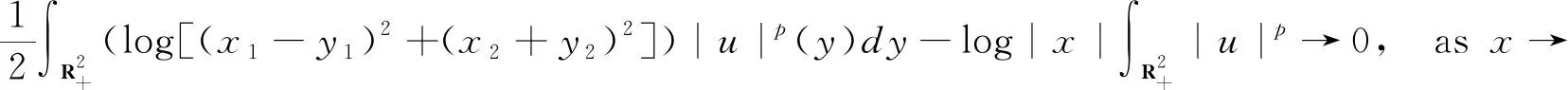
Here, we viewu∈Xodddefined on the upper halfspace. We will use this asymptotics in the proof of axial symmetry.

The following is the general Mountain Pass Lemma for Cerami sequence, see in [15].

Lemma 2.5AssumeXis a Banach space,Mis a metric space,M0⊂Mis a closed subspace, Γ0⊂C(M0;X). Define

Γ∶={γ∈C(M;X):γ|M0∈Γ0}.

IfI∈C1(X;R) satisfies

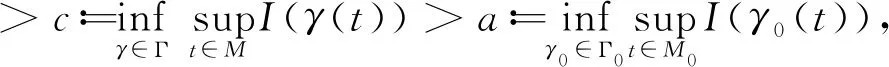
1.c-2ε≤I(u)≤c+2ε;

2. dist(u,γ(M))≤2δ;

3 Proof of Theorem 1.1

We use the idea of [6,10]. First we verify the Cerami compactness property of the action functional on the closed subspaceXodd. Then using the Mountain Pass Lemma 5, we can creat the Cerami sequence. Hence by the compactness, we get a critical point inXodd. Accordding to the Palais’ principle of symmetric criticality (see [25]), it is a critical point inX.

The two propositions can be seen in [10] forp=2 and in [6] forp≥2. Based on this two propositions, we can verify the Cerami compactness property for the action functional.

Lemma 3.3Let (un)⊂Xoddsatisfy

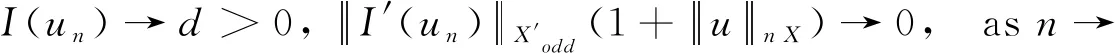
(3.1)

Then up to a subsequence, there exist points (xn)⊂Z2such that

un(·-xn)→ustrongly inXodd, asn→∞,

for some nonzero critical pointu∈XoddofI.

Now we give a refined and rigorous proof for allp≥2 for this key lemma.

ProofFor clarity, we divide the proof into several steps.

Step 1. If (un) satisfies condition (3.1), then (un) is bounded inH1. In fact, we have

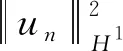
Step 2. We claim (un) is non-vanishing:

If not, by Lion’s vanishing lemma (see [27,30]), for eachs>2 we haveun→0 inLs. From

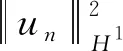
we get

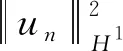
Substituting it intoI(un) yields

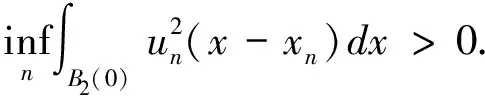
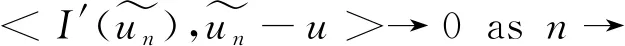
In fact, by theZ2-translation invariance, we have

Now, we estimate the last two terms in the following way:

whereA={|x-xn|≥|xn|},B={|x-xn|≤|xn|}. Then we chooseδ∈(0,1), setD1={|x-xn|≤δ}∩B,D2={δ≤|x-xn|≤|xn|}, thus each term is bounded by a constant independeent ofn:

Hence the above estimates yield

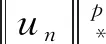
Sinceu≡0, we get

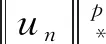
Combining the two estimates, we have

Then by the assumption (3.1) in Lemma3.3, we have

as claimed.

But on the other side, we get

Estimating each term yields

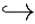
Now we estimateV′1.

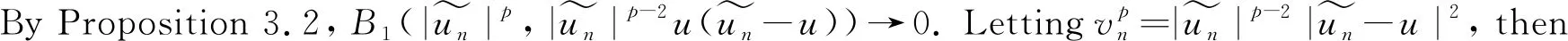
and we get

Now, applying Lemma 2.1, we have

Step 5. We proveuis the critical point:I′(u)=0. This can be easily checked.

Letv∈Xodd. As we have already shown

hence =0, which completes the proof.

Proof of Theorem 1.1(1)cmp,odd≥cmp>0 holds obviously.

(2) First we use the Mountain Pass Lemma 2.5 to construct the Cerami sequence (un)⊂Xodd, then we can extract a subsequence converging to a nonzero critical pointuwithI(u)=cmp,oddby applying the Cerami compactness property of Lemma 3.3 for the action functional. By Palais’ principle of symmetric criticality, we seeuis a critical point inX, and satisfies the corresponding properties of Lemma 2.3.

(3) First we notice thatcg,odd≥codd=cmm,odd≥cmp,odd, and alsocg,odd≤cmp,odd, socg,odd=codd=cmm,odd=cmp,odd. The equalitycodd=cmm,oddfollows by the monotonicity ofI(tu) fort(see [6]).

(4) This is obvious since all the ground state solutions have a constant sign (see [6]), and it can not be zero on the {x=(x1,x2):x2=0}.

4 Proof of Theorem 1.2

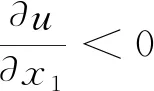
Proposition 4.1For everyv∈Xodd(R2), we have

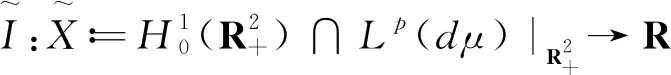
In pariticular, ifuis the minimal action odd solution, then

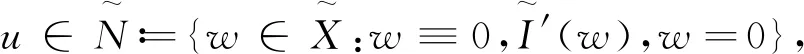
and

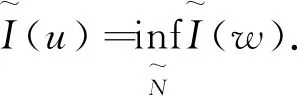
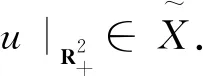
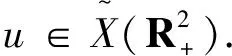
(4.1)

whereH=H1+H2is defined by

Recall that we have shown in Remark 2.4 that

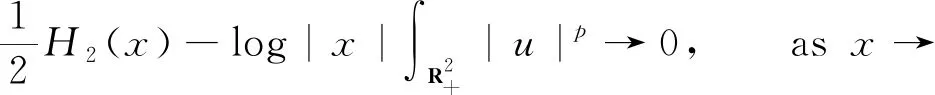
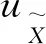
Proposition 4.2H2(x)=F(x)-G(x), whereF,Gare nonnegative functions bounded by

ProofThis is a regular computation. First we define the spherical cap over the upper half plane as:

Then we have

We estimateF(x) andG(x) in the following way.

and

The proof is complete.

Now we can prove

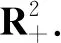
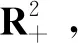
Proposition 4.4Forx∈Σλ, we have

ProofWe check it directly.

Substituting the above results intoLλ∶=H1(xλ)-H1(x) andMλ(x)∶=H2(xλ)-H2(x), yields the integral representations.

Proof of Theorem 1.2By the Euler-Lagrange equation (4.1), we knowwλ=uλ-usatisfies the equation

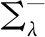
Our aim is to show this set is empty to givewλ=uλ-u≥0, and then letTλarrive at some limiting positionλ0to getwλ0(x)=uλ0(x)-u(x)=0, the desired symmetry property. We divide this process of moving plane into two steps.

Step 1. Start moving the plane fromλ=-∞.

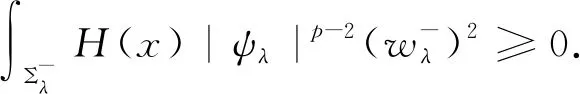
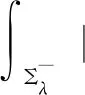
(4.3)

So by the Hardy-Littlewood-Sobolev inequality, we have

Hence

Applying Lemma 2.1, we have

So we have the estimates for the second term in (4.3):

Now by takingσ→0 andλnegative enough we get

Combining the above two estimates, we arrive at

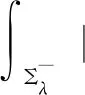
Step 2. Move the plane to the limiting position.

Defineλ0∶=sup{λ|wμ≥0 for allμ≤λ}. Then by the same argument as in Step 1 from the right directionx1=+∞, we seeλ0<+∞. Now, we provewλ0=uλ0-u=0 to get the axial symmetry. We show this by contracdiction. If not, we prove there exists anε>0 small enough such that for allλ∈(λ0,λ0+ε),wλ≥0, which is contradicted with the definition ofλ0.

Suppose nowwλ0≡0. Thenwλ0≥0 andwλ0(x0)>0 for somex0∈Σλ0. By the integral representation ofLλ0andMλ0, we seeLλ0<0 andMλ0<0. Then by the Euler-Lagrange equation ofwλ0, we have

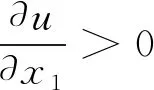
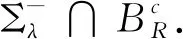
Acknowledgement.The author Zhang Yang is supported by the Postdoctoral Scientific Research Foundation of Central South University and appreciates the help from Professor Jiao Yong.