Global Gap Phenomenon of an Abstract Willmore Type Functional

Liu Jin

(College of Systems Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract For an n-dimensional submanifold in an (n+p)-dimensional unit sphere φ:Mn→Sn+p, let S and H2 denote the square length of second fundamental form and mean curvature vector of φ respectively. The function ρ=S-nH2 is called a Willmore invariant. Together with a function F:[0,+∞)→R, an abstract Willmore functional can be defined as which measures how it deviates φ(M) from a totally umbilical submanifold and generalizes the well-known classic Willmore functional. Its critical point is called the W(n,F)-Willmore submanifold which has been widely explored such as the first variational equations, the examples and pointwise gap phenomenon of critical points. In this paper, based on Simons’ type integral inequalities and some trickly estimates, a global gap phenomenon is derived out. It can be seen that there is a wide difference between the pointwise and global gap phenomenon.

Key words Willmore conjecture W(n,F)-Willmore type functional Willmore conjecture Simons’ type inequality Pointwise gap phenomenon Global gap phenomenon

1 Introduction

Letφ:Mn→Sn+pbe ann-dimensional compact without boundary submanifold in a unit sphere. Choose an orthonormal frame fields

{e1,…,en,en+1,…,en+p}

alongMsuch that {e1,…,en} are tangent toMand {en+1,…,en+p} are normal toM. Their dual frame fields are {θ1,…,θn} and {θn+1,…,θn+p} respectively. Obviouslyθn+1=…=θn+p=0 when they are restricted overM. Throughout this paper, we always use Einstein’s convention which says that the same indices stand for sum, and the convention about range of indices:

1≤A,B,C,D,…≤n+p,1≤i,j,k,l,…≤n,n+1≤α,β,γ,δ,…≤n+p.

LetIIdenote the second fundamental form of the immersionφ:M→Sn+p(1). Write

and define

In differential geometry, there is a famous classic Willmore functional for submanifold in unit sphereφ:Mn→Sn+p(1) which is defined as

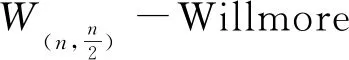
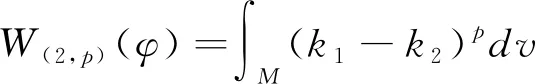
Motivated by the work mentioned above, in order to establish a universal frame including all above different functionals. In the serial papers [15-17], we studied an abstract functional calledW(n,F)-Willmore functional of submanifoldφ:Mn→Sn+p(1) which is defined as

where we always assume that the abstract functionFsatisfies

F:u→F(u),F∈C3([0,+∞)→R).

The critical points of this functional are calledW(n,F)-Willmore submanifolds. In geometric meaning,W(n,F)-Willmore Functional abstractly measures how it deviatesφ(M) form a totally umbilical submanifold and generalizes the well-known classic Willmore functional. In those papers, the first variational equations, the examples of critical points and some other results are obtained.

It is well known that the Simons’ integral inequality [18] plays an important role in the study of minimal submanifold. It says that ifMis ann-dimensional compact minimal submanifold in the (n+p)-dimensional unit sphereSn+p(1), then

For the classic Willmore submanifold, in [6-9] Li proved a Simons’ type integral result which says ifMis ann-dimensional compact classic Willmore submanifold in the unit sphereSn+p(1), then

For theW(n,F)-Willmore submanifold, in [16], by the same techniques used in [6-10,13,14], we established a Simons’ type integral result which says ifMis ann-dimensional compact classic Willmore hypersuface, surface, or submanifold in the unit sphereSn+p(1), then it holds the following three theorems.

Theorem 1.1([15-17]) LetMbe ann-dimensional compactW(n,F)-Willmore submanifold in the unit sphereSn+p(1). Whenp=1, one has

+nH2(nF(ρ)-2ρF′(ρ))-2ρ(ρ-n)F′(ρ)]dv=0.

Theorem 1.2([15-17]) LetMbe ann-dimensional compactW(n,F)-Willmore submanifold in the unit sphereSn+p(1). Whenp≥2 andF′(ρ)≥0, one has the following Simons’ type inequality

Theorem 1.3([15-17]) LetMbe ann-dimensional compactW(n,F)-Willmore submanifold in the unit sphereSn+p(1). Whenp≥2 andF′(ρ)≥0, one has the following Simons’ type inequality

In fact, for the functionalW(n,1), by the techniques developed in [21], Xu and Yang in [20] derived out a global phenomenon which says that ifMis ann-dimensional compact without boundaryW(n,1)-Willmore submanifold in an (n+p)-dimensional unit sphereSn+p(1) withn≥3, then there exists an explicit constantA(n) depending only on the dimensionnsuch that if

thenMmust be totally umbilical.

The main purpose of this paper is to generalize the above results to theW(n,F)-Willmore submanifold case. The rest of this paper is organized as follows. In section 2, some trickly estimates which are useful in the discussion of global gap phenomenon are derived. In section 3, we establish a global gap phenomenon which says if the integral norm ofρcontrolled from above, thenMmust be a totally umbilical submanifold. For particular functionsF, the results we obtained in the corollaries coincide with the results in [20] and generalize them.

2 Some estimates

Letφ:Mn→Sn+p(1) be ann-dimensional compact without boundary submanifold in an (n+p)-dimensional unit sphere, and let

s=(s1,…,sn,sn+1,…,sn+p),σ=(σ1,…,σn,σn+1,…,σn+p)

be the orthonormal local frame fields ofTSn+p(1) andT*Sn+p(1) respectively. Then

e=(e1,…,en,en+1,…,en+p)=φ-1s

is the orthonormal local frame fields of the pull back vector bundleφ-1TSn+p(1) overMsuch that {e1,…,en} are tangent toMand {en+1,…,en+p} are normal toMdue to

φ-1TSn+p(1)=TM⊕T⊥M.

Usingωto denote the connection form overTSn+p(1), by the pull back operation, we can assume the following notations:

φ*σ=θ,φ*σi=θi,φ*σα=θα,

Thus one can derive that {θi} are the orthonormal frame fields ofT*Mand

θn+1≡…≡θn+p≡0

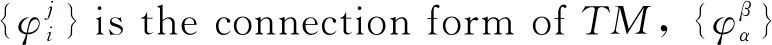
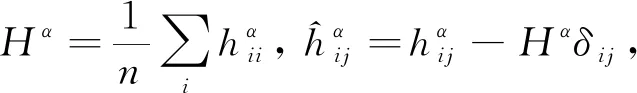
Lemma 2.1([21,20]) Letφ:Mn→Sn+p(1) be a submanifold, one has the estimate

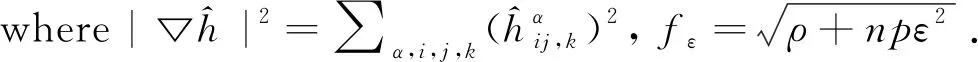
ProofLet

and

Obviously, one has

Thus, for a fixed indexα∈[n+1,n+p], we have

This is to say

So

i.e.

Thus we have

The proof is complete.

Lemma 2.2([20-21]) Letφ:Mn→Sn+p(1) be a compact submanifold withn≥3. Then for any functiong∈C1(M) withg≥0 andt>0,gsatisfies the following inequality

where

andc(n) is a positive constant depending only on the dimensionn.

ProofFrom [21] and [22], we have

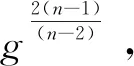
Through a directly calculation and Hölder’s inequality, we obtain

i.e.

Square both sides of the above inequality, we obtain

i.e.

Thus we complete the proof.

3 Global gap phenomenon

Based on the Simons’ type integral inequalities in Theorems 1.1, 1.2, 1.3 and the estimates derived in Lemmas 2.1, 2.2, we can establish the global gap phenomenon.

Theorem 3.1LetMbe ann-dimensional compact without boundaryW(n,F)-Willmore submanifold in an (n+p)-dimensional unit sphereSn+p(1) withn≥3. AssumeFsatisfies the following conditions

(C1)F′(u)>0,∀u∈(0,+∞);

(C2)F″(u)≥0,∀u∈[0,+∞);

(C3)uF″(u)≤2F′(u),∀u∈[0,+∞);

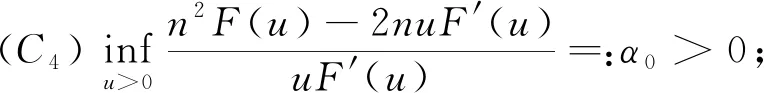
(C5)F′(u)u=0⟺u=0.

Then there exists an explicit constantA(n,α0) depending only on the dimensionnand the parameterα0ofFsuch that if

thenMmust be totally umbilical.

ProofSetting

since

from Theorem 1.1, Theorem 1.2 and Theorem 1.3, we can derive out

-ηρ2F′(ρ)+2nρF′(ρ)]dv≤0.

-ηρ2F′(ρ)+2nρF′(ρ)]dv≤0.

(1)

By Lemma 2.1, we know

substituting it into (1), one has

(2)

Setting

by a directly calculation, we have

By conditions (C2) and (C3), we have

Thus, from (2), we obtain

i.e.

Using Lemma 2.2 we immediately get

i.e.

By condition (C4), if

then

If

then

So by taking

we get

then using Hölder’s inequality, we obtain

i.e.

Therefore we conclude that if

then

By condition (C5), we knowρ≡0, i.e.Mis totally umbilical. Here

Fix the functionFand take

then we complete the proof.

Corollary 3.1([20]) LetMbe ann-dimensional compact without boundaryW(n,1)-Willmore submanifold in an (n+p)-dimensional unit sphereSn+p(1) withn≥3, i.e.,F(u)=u. Then there exists an explicit constantA(n) depending only on dimensionnsuch that if

thenMmust be totally umbilical.

ProofObviously functionF(u)=usatisfies the conditions in Theorem 3.1.

thenMmust be totally umbilical.

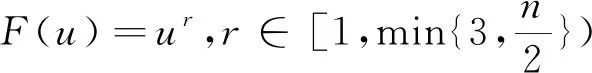
Remark 3.1Corollary 3.1 coincides with the result in [20] and Corollary 3.2 generalizes it.

4 Conclusion

In this paper, based on the Simons’ type integral inequalities derived out in [15-17] and some trickly estimates, under some suitable conditions of functionF, we established the global gap phenomenon forW(n,F)-Willmore submanifolds. Without any surprise, there is a wide difference between the pointwise and global gap phenomenon not only techniques used but also results obtained which show us an interesting picture about the critical points of abstract Willmore type functionls.