一类空间分数阶扩散方程的预处理方法*

嵇雯蕙

(昆明理工大学理学院,昆明,650000)

1 引言

随着自然科学和生产技术的不断发展, 微分方程逐渐成为现代科学技术中分析问题和解决问题的一个强有力的工具. 近几十年来, 分数阶微分方程在水文、生物、物理、化学、金融等学科有着广泛的应用[1-5]. 分数阶微分方程之所以能够在诸多领域得到广泛的应用, 主要是因为分数阶微分算子具有非局部特征, 从而能更精确地反映一些物理现象.

在空间扩散模型中, 用分数阶导数代替空间扩散二阶导数, 将导致更强的扩散. 最近, Mao and Shen[6]考虑了一类基于阶数α∈(1/2,1)左右导数的分数阶微分算子的偏微分方程, Xu, Sun, and Sheng[7]从变分的角度考虑了平衡中心分数阶导数, 它们保持了所需的变分性质以及L2框架上的对称双线性形式. 由于分数阶偏微分方程的解析解往往很难用简单的函数表示, 因此研究分数阶偏微分方程的数值方法和理论分析就显得尤为重要.

本文的主要目的是研究求解空间分数阶扩散方程的有限差分格式离散系统的快速迭代方法.

2 问题的模型

我们考虑的空间分数阶扩散方程(FDEs)如下[9]：

(2.1)

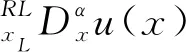
为了对方程 (2.1) 建立差分格式, 我们先给出如下几个引理.

引理1[12]假设u(x)∈C2[xL,xR], 令

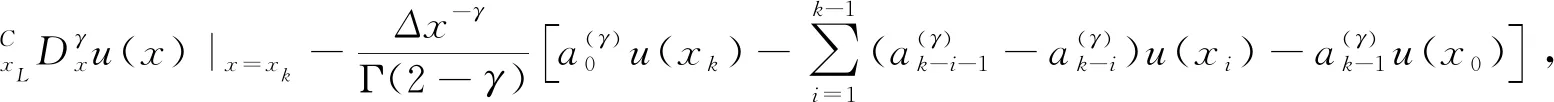
则

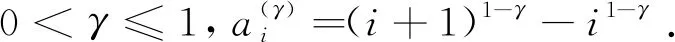
利用同样的数值微分方法, 可以得到右Caputo分数导数的以下推论.

推论1假设u(x)∈C2[xL,xR], 令

则

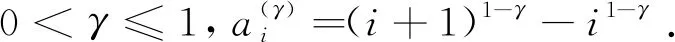
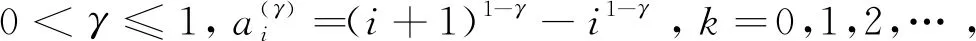
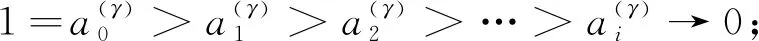
由

以及引理1和推论1, 我们可以得到Riemann-Liouville分数导数的差分逼近.

3 有限差分格式的建立

类似文献[14]的离散方法, 我们把方程 (2.1) 离散如下.

将区间[xL,xR]均匀分为n+1个等分, 空间步长Δx=(xR-xL)/(n+1), 则xi=xL+iΔx, 其中i=0,1,…,n+1. 同理, 将[0,T]均匀分为m个等分, 时间步长Δt=T/m, 则tj=jΔt, 其中j=0,1,…,m.

令

通过引理1和2以及推论1, (2.1) 中FDEs对应的隐式有限差分格式如下:

为了将数值格式改写为矩阵形式, 令

其中

于是, 我们得到有限差分格式的矩阵表达式

A(j)u(j)=ηu(j-1)+Δx2α(f(j)-σ(j)),j=1,2,…,m,

(3.1)

其中系数矩阵A(j)为

(3.2)

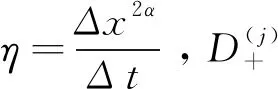
其中

(3.3)

关于 (2.1) 离散的详细情况, 见文献[14].

我们将式 (3.3) 代入 (3.2) 化简后, 系数矩阵A(j)变为

(3.4)

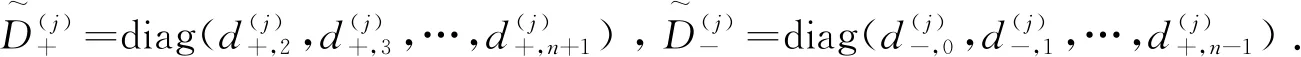
4 问题的求解

本节主要任务是求解线性方程组 (3.1). 由于系数矩阵A(j)是非对称的, 我们考虑应用Krylov子空间方法的GMRES法来求解.

下面先简单地介绍一下GMRES方法[15].

4.1 GMRES法

设要求解的线性方程组为

Ax=b.

任取一n维实向量x(0), 令x=x(0)+z, 则上述方程组等价于

Az=r(0),

(4.1)

其中r(0)=b-Ax(0). 故下面直接讨论(4.1)的求解问题.

从r(0)开始, 构造一组相互正交且范数为1的向量v(1),v(2),…,v(m).

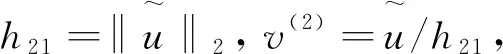
类似地, 计算v(3)的过程如下:

(1)计算u=Av(2),h12=(u,v(1)),h22=(u,v(2));

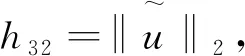
继续这一过程, 经过m步, 即可得到矩阵Vm=[v(1),v(2),…,v(m)].

从上述过程可以发现:

Av(1)=h11v(1)+h21v(2),

Av(2)=h12v(1)+h22v(2)+h32v(3),

…

Av(m)=h1mv(1)+h2mv(2)+h3mv(3)+…+hm+1,mv(m+1).

写成矩阵形式, 即

其中

假设存在一个y∈Rn满足z=Vmy, 则有

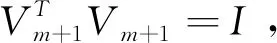
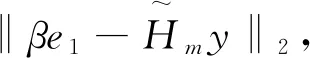
分解得到.

具体算法如下[15]：

GMRES算法1. 计算r0=b-Ax0, β∶=‖r0‖2, v1∶=r0/β2. For j=1,2,…,m, Dowj∶=AvjFor i=1,…,j, Dohij∶=(wj,vi)wj∶=wj-hijviEnd Dohj+1,j=‖wj‖2. If hj+1,j=0 set m∶=j and go to 3vj+1=wj/hj+1,jEnd Do3. 定义(m+1)×m的Hessenberg矩阵H-m=hij 1≤i≤m+1,1≤j≤m4. 计算ym, 极小化‖βe1-H-my‖2, 且xm=x0+Vmym.

4.2 预条件子的建立

为了提高收敛速度, 我们建立预处理的GMRES方法. 针对系数矩阵的结构,我们分别构造带状矩阵、改进的带状矩阵、Strang循环矩阵以及T. Chan循环矩阵作为预处理矩阵M来逼近矩阵A(j), 使得M-1A(j)的特征值聚集在1附近, 从而达到收敛速度提高的效果. 四种不同的预处理矩阵的构造如下:

(1)带状矩阵

此时,预处理矩阵M为

(4.2)

易证此矩阵为三对角阵. 而我们知道三对角阵的线性方程组容易求解, 可以利用“追赶法”求出来, 所以M的构造合理.

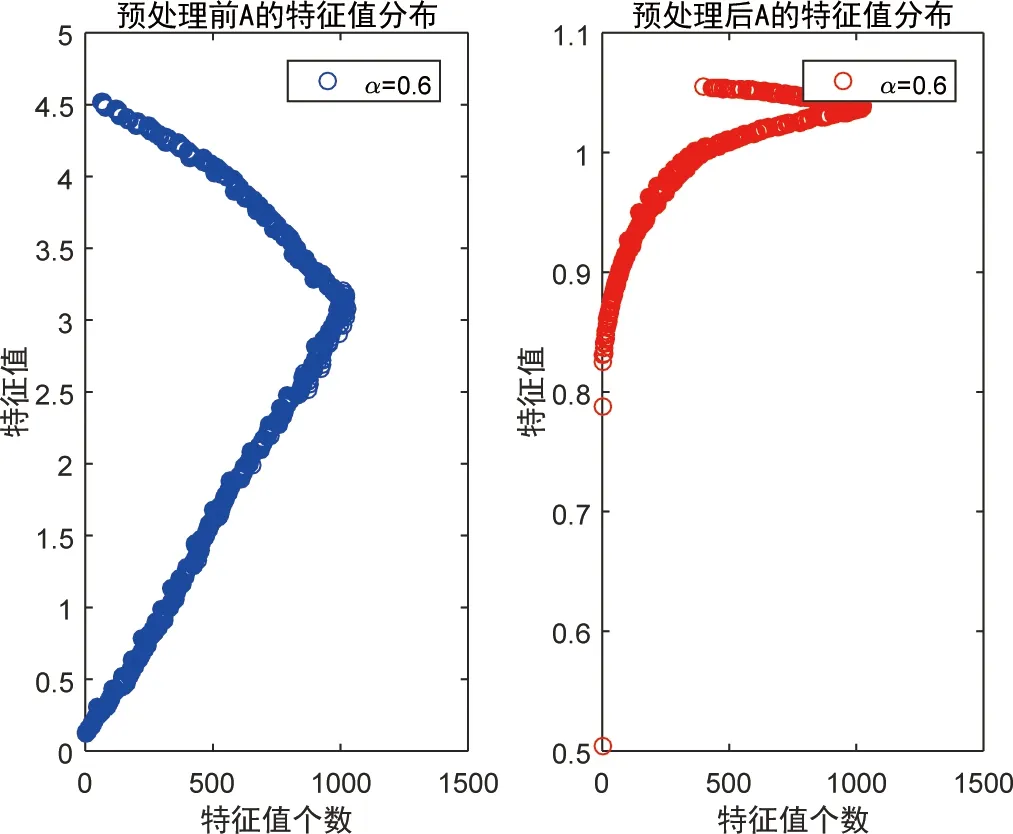
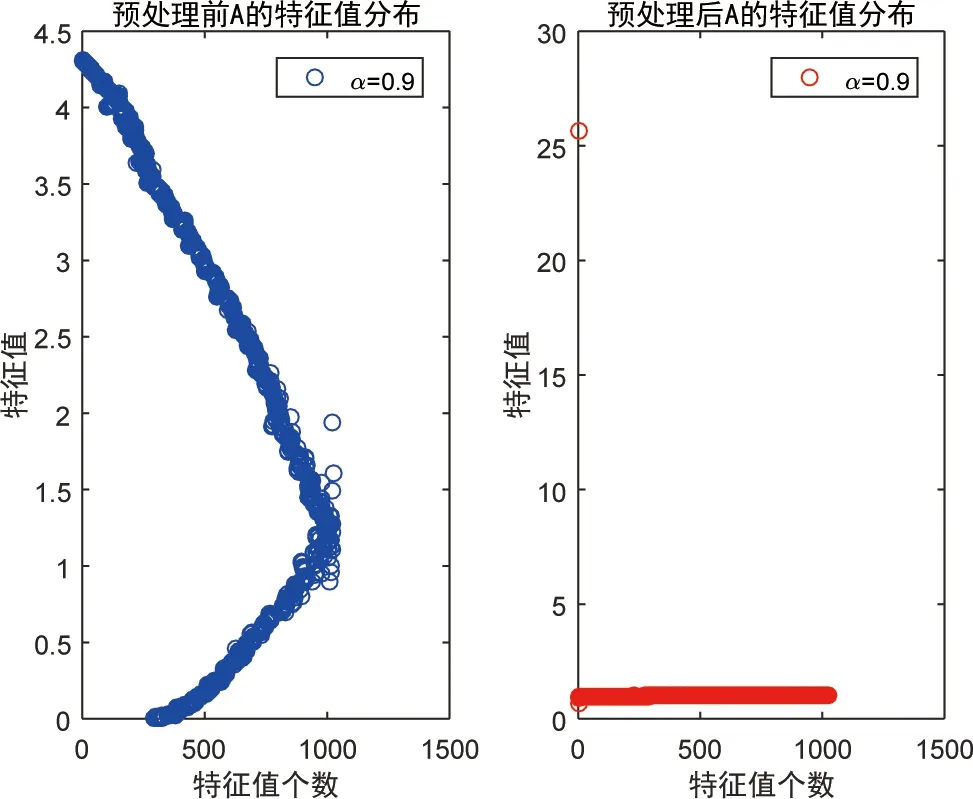
为了更直观地说明预处理后矩阵谱的聚集情况, 基于不同的α, 我们分别给出预处理前后系数矩阵特征值分布的对比图如下(其中n=1024).

由图1和图2可见, 对于不同的α, 预处理后矩阵谱的普遍聚集在1附近, 只有个别点距1较远.

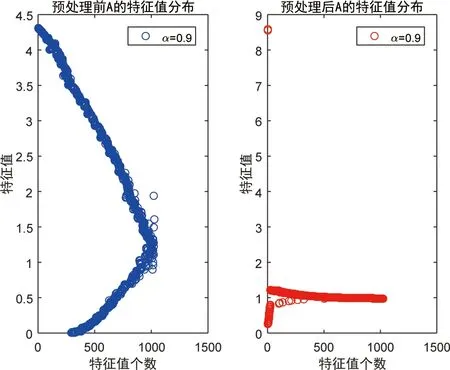
图2 α=0.9

(2)改进的带状矩阵

由公式(3.4), 我们注意到系数矩阵是由对称正定矩阵和低秩矩阵L构成的. 为了构造一个更逼近系数矩阵的M, 对公式(4.2)作如下改进:

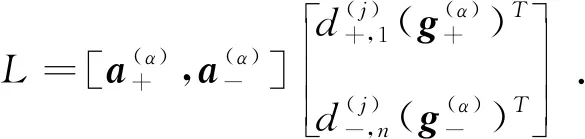
因为一个可逆矩阵加上一个低秩矩阵的逆也是容易求的, 若记

令

L=XGY,

其中X是n×r,Y是r×n,G是r×r的非奇异矩阵,r是L的秩，则

M-1=C-1-C-1X(G-1+YC-1X)-1YC-1.

故这里的M构造合理.

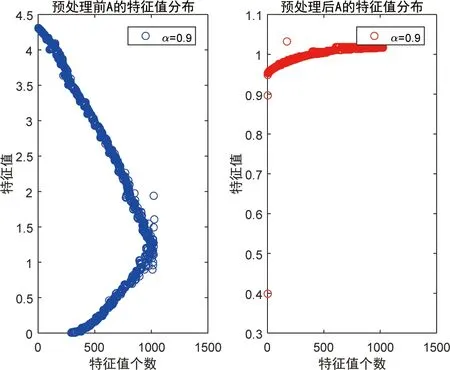
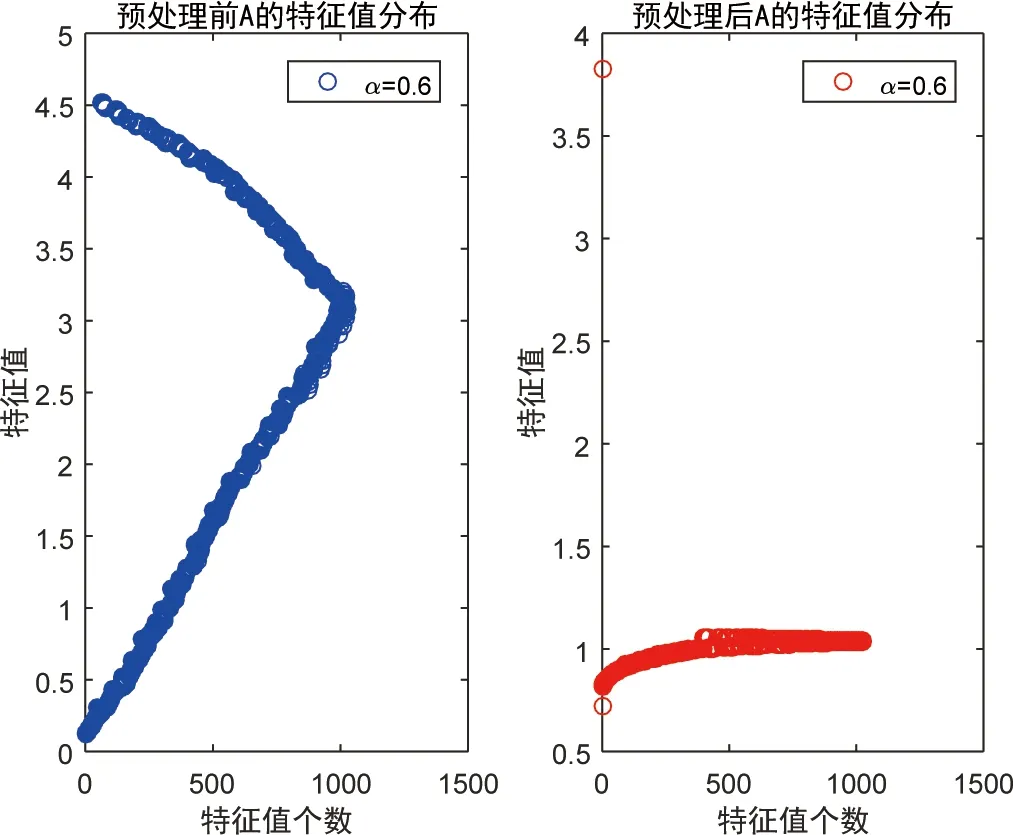
当预条件子为改进的带状矩阵时, 预处理前后的特征值分布图如下.

由图3和图4可见, 采用改进后的带状矩阵, 个别远点消失, 所有的特征值都聚集在1附近.

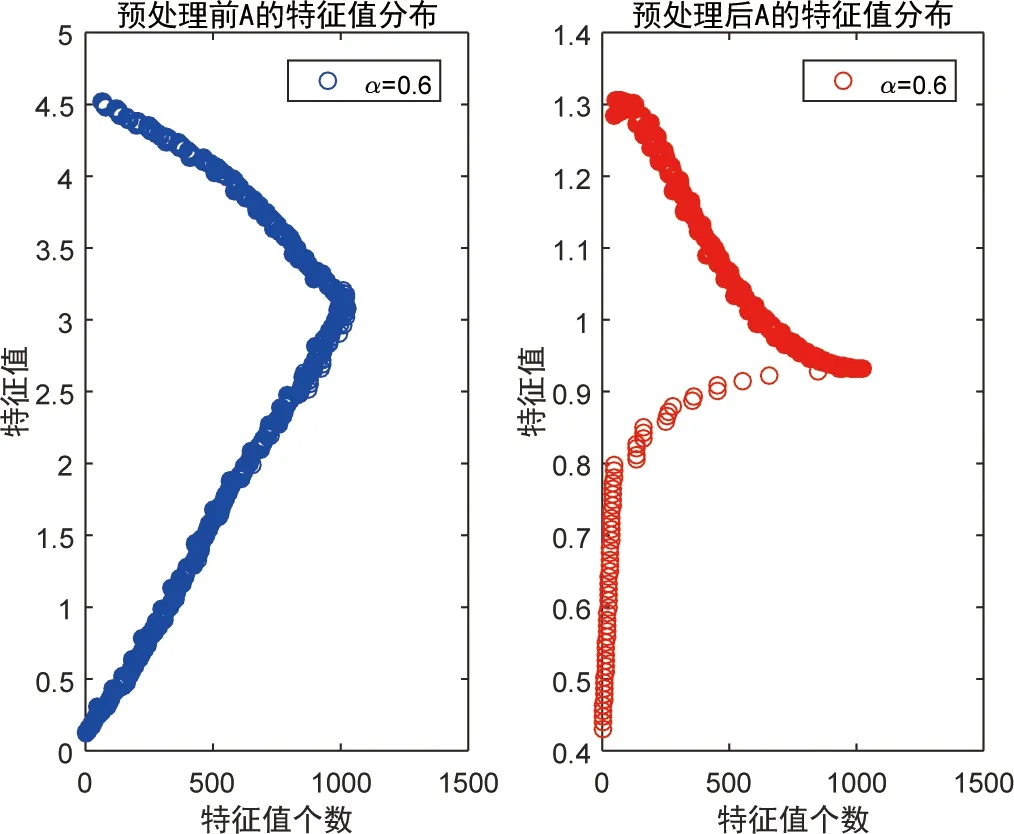
图3 α=0.6

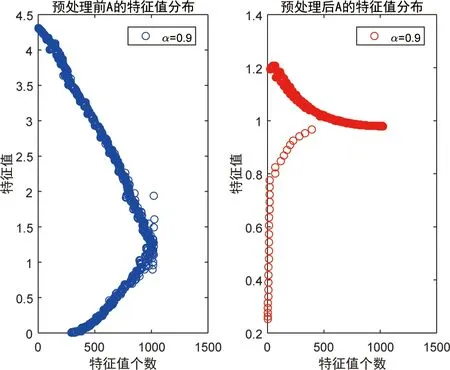
图4 α=0.9

(3)Strang循环预处理矩阵

(4.3)

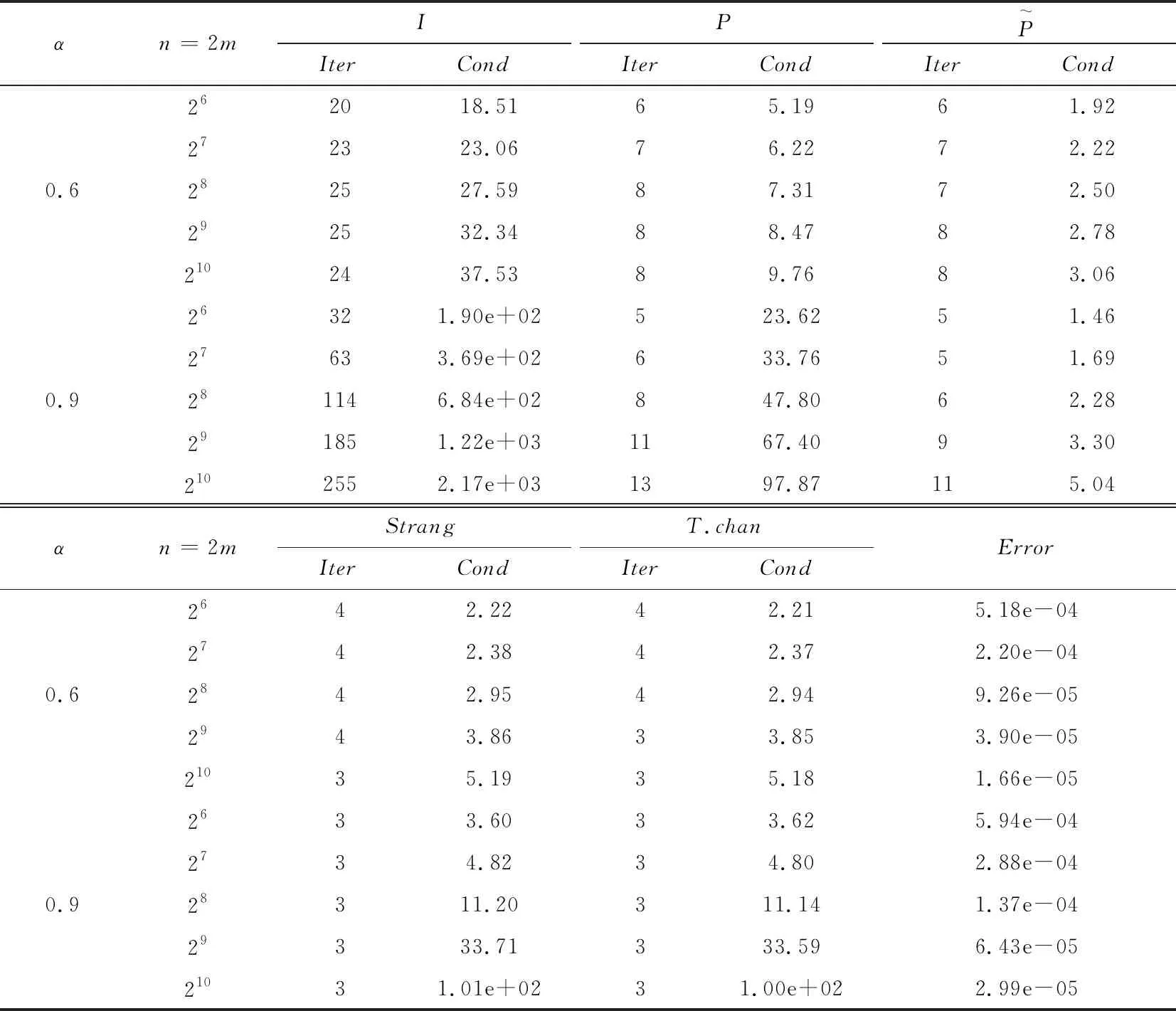
对于实Toeplitz矩阵B=[bj-k]0≤j,k

s(B)=[sj-k]0≤j,k

其中,sj是Strang预条件子对角线上的元素, 且有：

相对于文献[14]中的预处理矩阵, 此处的预处理矩阵更逼近A(j). 当预条件子为Strang预处理矩阵 (4.3) 时, 预处理前后系数矩阵的特征值分布图如下.

通过图5和图6, 我们可以清晰地看到基于该预条件子预处理后系数矩阵的特征值更集中且在1附近.

图5 α=0.6

图6 α=0.9

(4)T. Chan预处理矩阵

T. Chan预条件子c(B)=[ck-j]0≤k,j

当预条件子为T. Chan预处理矩阵时, 预处理前后系数矩阵的特征值分布图如下.

由图7和图8可见, 预处理后系数矩阵的特征值显然在1周围集中, 故该预条件子选取合理.

图7 α=0.6

图8 α=0.9

5 数值实验

为了验证算法的有效性, 我们考虑如下的方程[14]

其中扩散系数为d+(x,t)=(1-x)α,d-(x,t)=xα,源项为

其中

方程的精确解为u(x,t)=e-tx2(1-x)2.

表1 四种不同的预条件子的比较

结果表明, 在不进行预处理的情况下, GMRES方法收敛需要多次迭代且随着n变大迭代次数增多, 而预处理的结果迭代次数更少更稳定且条件数大大减少. 以上的预条件子中, Strang和T. Chan循环预处理条件子处理效果最好.

6 总结

本文采用预处理的GMRES方法, 对一类FDEs(2.1)产生的离散线性系统进行求解. 数值试验证明了所提出的预处理方法的有效性.

但是, 如果在由FDEs(2.1)产生的离散化方案中考虑其变分性质或有限体积法, 那么得到的线性系统有可能是对称正定的. 然后, 可以采用共轭梯度法来有效地解决这些问题. 因此, 在今后的研究中, 我们应进一步研究这类FDEs的数值格式以及相关的预条件.