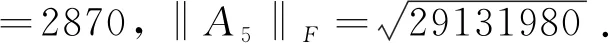含Pell数和Pell-Lucas数乘积的斜循环矩阵的行列式及其性质*

李笑丽 何承源 雷林

(西华大学理学院,成都，610039)

1 引言

循环矩阵在非线性控制系统、预处理、信号处理、图像处理、Toeplitz矩阵等问题中起着重要的作用[1-3]. 近年来, 矩阵理论工作者对包含著名数列的循环矩阵进行了一系列的研究, 如循环矩阵的行列式、范数、逆矩阵及扩展式等[4-12]. 文献[13]给出了以Fibonacci数和Lucas数之积为元素的斜循环矩阵的行列式、逆矩阵和范数等. Zheng与 Shon[14]研究了广义Lucas斜循环矩阵的精确行列式和逆矩阵. Bozkurt[10]给出了带有Pell和 Pell-Lucas数列的经典循环矩阵的行列式和逆矩阵.

受上述研究的启发, 本文将对以Pell数和Pell-Lucas数之积为元素的斜循环矩阵、左斜循环矩阵的行列式、范数及扩展式的上下界进行研究.

2 预备知识

定义2.1[15]已知Pell数列{Pn}：Pn+2=2Pn+1+Pn,其中P0=0,P1=1,P2=2,n≥0；Pell-Lucas数列{Qn}：Qn+2=Qn+1+Qn,其中Q0=2,Q1=2,Q2=6,n≥0. 定义新数列{ζn}如下：

ζn+2=6ζn+1-ζn,n≥1,

(2.1)

其中ζ1=2,ζ2=12.ζn是第n个Pell数和第n个Pell-Lucas数之积, 其前几项如下表：

表1 第n个Pell数和第n个Pell-Lucas数之积

新数列{ζn}的Binet公式如下：

(2.2)

其中α和β是特征方程x2-6x+1=0的两个不同的根.

定义2.2以ζ1,ζ2,ζ3,…,ζn为元素的n阶斜循环矩阵为

(2.3)

定义2.3以ζ1,ζ2,ζ3,…,ζn为元素的n阶左斜循环矩阵为

(2.4)

引理2.1[7]设每个矩阵Xn=(Hk,n-1,Hk,n,Hk,n,Hk,n+1)的项为广义k-Horadam数. 则当n≥1时有

|Xn|=(-g(k))n-1(a2g(k)+abf(k)-b2).

引理2.2设ζn是第n个Pell数和第n个Pell-Lucas数之积，则有

(2.5)

(2.6)

(2.7)

(2.8)

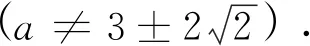
因此

(2.9)

(2)由(2.1)有

(2.10)

于是, 由(2.9)和(2.10)得

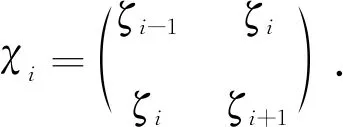
对{ζn}有

(2.11)

从而, 从(2.11)可得

所以

(4)令

(2.12)

由(2.1)和(2.12)以及

a2Sn=ζ1a3+ζ2a4+…+ζnan+2,

6aSn=6ζ1a2+6ζ2a3+…+6ζnan+1

可得

(a2-6a+1)Sn=ζnan+2-ζn+1an+1+2a,

因此

引理2.3[4]斜循环矩阵和左斜循环矩阵满足下列关系式

SCirc(a1,a2,a3,…,an)=ΔSLCirc(a1,a2,a3,…,an),

定义2.4[11]矩阵An的最大列和范数‖An‖1, 最大行和范数‖An‖∞和Frobenius范数‖An‖F定义为：

这里‖A‖F是Frobenius范数, trA是A的迹.

引理2.5[17](1)若A=(aij)是正规实循环矩阵, 则

s(A)≥(1/(n-1))|∑i≠jaij|.

(2)若A是Hermitian矩阵, 则s(A)≥2maxi≠j|aij|.

3 斜循环矩阵的行列式、范数及其扩展式的上下界

定理3.1An的行列式为

(3.1)

证明由矩阵An的定义, 可得 detA1=1,detA2=148以及detA3=346320.

当n>3时, 构造矩阵

和

则

(3.2)

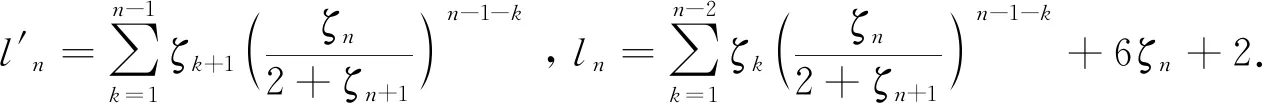
(3.3)

(3.4)

对(3.2)式两端取行列式得

推论3.1An可逆.

证明由定理3.1易知结论成立.

定理3.3An的最大列和范数‖An‖1, 最大行和范数‖An‖∞和Frobenius范数‖An‖F为：

(3.5)

(3.6)

证明由定义2.4, 式(2.5)及式(2.7)即可得

定理3.4An的扩展式s(An)的上、下界如下：

(3.7)

证明已知An的迹trAn=nζ1=2n,An的非对角线元素之和

由式(2.5)和式(2.6)可得

4 左斜循环矩阵的行列式、范数和其扩展式的上下界

定理4.1A″n的行列式为

(4.1)

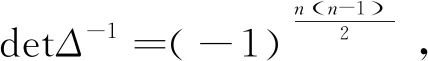
推论4.2A″n可逆.

定理4.3A″n的最大列和范数‖A″n‖1, 最大行和范数‖A″n‖∞和Frobenius范数‖A″n‖F为：

(4.2)

(4.3)

证明利用与定理3.3相同的证明方法即可得结论.

定理4.4A″n的扩展式s(A″n)的上、下界如下：

证明因矩阵A″n是对称矩阵, 所以由引理2.4和引理2.5可知

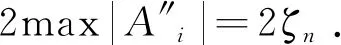
当n为奇数时, 有

又ζn+2=6ζn+1-ζn, 其中ζ1=2,ζ2=12, 因此

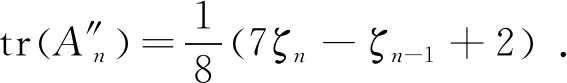
当n为偶数时, 有

tr(A″n)=ζ1-ζ1+ζ3-ζ3+…+ζn-1-ζn-1=0.

综上即可得

5 数值例子

解由MATLAB中求矩阵的行列式公式计算得detA5=7.6087e+16. 根据式(3.1)可得detA5=7.6087e+16. 由定义2.4可得

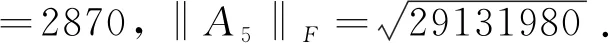
又根据式(3.5)及式(3.6)可得A5的三种范数

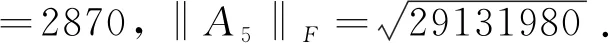
解在MATLAB中输入矩阵, 再用求矩阵行列式的公式, 可得detA″5=7.6087e+16,又由式(4.1)可得detA″5=7.6087e+16. 由定义2.4可得

再由式(4.2)和式(4.3)可得