遗传算法优化前馈PID控制电液系统研究
吴晓莉,张 雷
(1.咸宁职业技术学院工学院,湖北咸宁437000;2.湖南科技大学机械工程学院,湖南湘潭411201)
电液比例系统由于具有成本低、环境适应性强、易于维护等优点,被广泛应用于制造和工程机械的运动控制、车辆运动控制及各类工业应用中[1-2]。比例阀作为电液比例系统的控制元件,与伺服阀相比,具有一阶更高的间隙和死区[3]。在大多数液压执行器中,气缸摩擦具有很强的非线性特性[4],这主要是由气缸内腔的气体压缩性和体积随温度变化引起。对于不对称执行机构,活塞上的压力轴承区域的差异会导致额外的复杂性。因此,通过使用便宜的设备来实现伺服器跟踪性能正成为控制领域新的研究趋势。鲁文其等[5]为提高拉削过程负载断续变化时拉床控制的精度,基于扰动辨识和补偿机理的自校正算法,实现了伺服系统的高精度控制,最大同步控制误差在40 μm;而唐敬东等[6]采用比例阀控制,以拉削速度为反馈量形成闭环控制,实现了类似伺服阀的控制性能。Mohanty等[7]通过使用伺服阀实现了与机器人手臂相对精确的梯形运动,该研究的重点是实现更快的系统响应。而Papadopoulos等[8]开发了一种在恶劣的林业环境下连续工作机械手,每个子系统都有一个比例阀和气缸组成,在0.05 Hz的情况下实现了复杂的3-DOF正弦运动跟踪。Sarkar等[9]将前馈作为时间的分段二次函数进行实时处理,进一步提高了电液系统的控制性能。虽然遗传算法在一般控制器设计环境中的应用已经进行了相当长时间的讨论,但其是前馈控制相结合,被证明在控制器设计中是相当有效的[10]。
为实现电液系统高负荷和高精度控制的目的,本文从气缸摩擦的静态模型出发,提出了对广义轮廓采用分段时间二次函数的合理性,设计了基于遗传算法(GA)优化的前馈PID控制器,用于自动确定控制器的增益和参数;除了对现有结果的优化性能进行评估外,还对典型的跟踪和调节需求组合的控制性能进行了研究,进一步对比了伺服控制器的控制性能。
1 系统原理和控制器结构
1.1 系统原理
电液比例驱动系统原理如图1所示。该系统主要由液压系统、控制系统和执行系统3部分组成。液压系统提供系统工作所需的动力,安全阀RV用于保持系统压力恒定。控制系统由上位机和工控机组成,通过工控机接收液压缸位移速度信号,并经过控制器处理后,输出反馈给气动比例阀。执行系统由单作用气缸S和双作用气缸D组成,弹簧用于提供气缸运动的负载,线性可变差动变压器(LVDT)提供活塞位移的控制反馈。
1.2 控制器结构
图2给出了单作用气缸S的前馈PID控制系统结构。如图2所示,控制器的输入yd是时间t的函数。活塞位移y通过LVDT测量获得,表示为yLVDT。由于气缸内的摩擦力对活塞运动有很强的非线性依赖性,将yd作为扰动变量(DV)反馈给前馈控制器。在控制器内,通过适当的信号发生器获得速度信号vd和加速度信号ad,用于计算前馈电压ef。反馈电压eb通过反馈控制器获得,将前馈信号和反馈信号输入到比例阀的控制线圈,获得其总电压为

图1 电液驱动系统原理图Fig.1 Schematic diagram of electro-hydraulic drive system

图2 前馈PID控制系统结构Fig.2 Structure of feed-forward PID control system

反馈电压通过PID控制器获得,表达式为
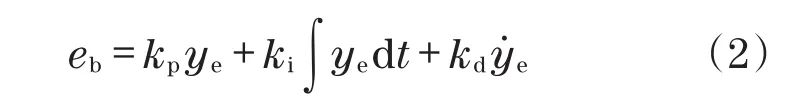
式中:kp,ki,kd分别为比例、积分、微分增益。
系统位移误差为

反馈控制器通常用于处理系统中,由于阀内部摩擦或液压源的可压缩性引起的弱非线性,而前馈控制主要用来补偿压差变化和气缸内的摩擦等强非线性。两者均需要获得活塞的运动速度,即

本文用静态模型[9]对这些非线性的补偿电压进行了简单的分析,忽略油液压缩性的影响,并考虑到阀的运动比活塞运动要快得多,因此,活塞速度与压力之间的非线性关系可以表示为

式中:CdA,CdB分别为阀口A和B的流量系数;Aa1,Aa2分别为气缸有杆腔和无杆腔的作用面积;Pp,PT分别为系统的供油压力和回油压力。
气缸活塞运动的摩擦力Ff,包含滑动摩擦、Stribeck摩擦和黏性摩擦,其模型为
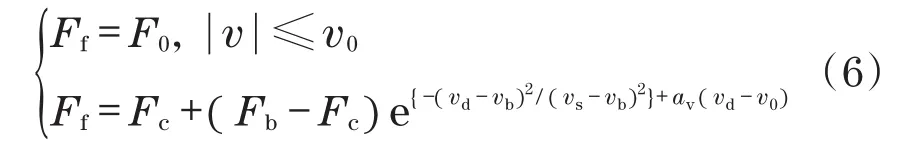
式中:F0为静摩擦力;v0为滑动速度;Fc为库伦摩擦力;vs为Stribeck速度;av为黏性摩擦系数;Fb为最大边界润滑摩擦,对应速度为vb。
这些非线性的影响,主要表现在系统的瞬态运动过程,系统加速度方程表示为

式中:ks为负载弹簧刚度;ma为负载质量。
该方程在活塞运动过程中可重新表示为

对方程做适当简化,系统摩擦力只保留静摩擦和黏性摩擦项。式(4)中的电压可表示为与e0成正比的常数,以及一个相对较小的项来补偿弹簧、惯性力和摩擦力。上述方程中加速和速度平方等清楚表明,前馈电压可近似为时间的二次函数。因此,本文将前馈电压表示为时间的二次函数,PID反馈用位移误差表示,以满足简单的前馈模型。
2 控制器设计
2.1 前馈控制器设计
前馈控制器的设计被描述为一个广义的时间周期T,如图3所示。该周期由i=1~8的8个持续时间段组成,分别表示为t1到t8。该平滑过渡方案可保证在跟踪和控制阶段之间的每一时刻都有有限的加速度。此外,线性轨迹在转换过程中会产生很大的加速度。任何奇数段前馈电压的线性变化确保了当活塞由于摩擦的黏滑性质而保持静止时,为克服静态摩擦所必需的活塞推力的平稳性。
与式(8)的讨论一致,前馈电压以分段方式获得,以便跟踪段i=2和6,其电压表示为
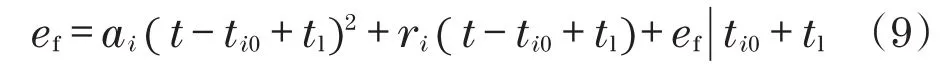
对于恒定和线性变化的电压段i=1,3,4,5,7和8,有

图3 前馈控制器设计的分段过程Fig.3 Segmental process of feed-forward controller design

式中:tl为用于补偿油液压缩性和安全阀的迟滞时间;ti0为第i段的开始;ai和ri为维度常数。
对于反馈电压恒定段,有

图3对任意周期c的复合跟踪控制可表示为
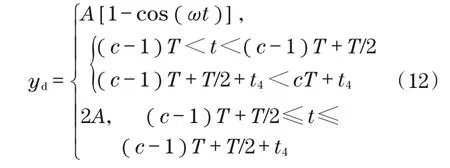
式中:A,ω分别为正弦跟踪信号的幅值和频率。
由式(12)表示的半周期正弦曲线可以作为平稳表示阶跃要求的内部参考模型。在一个周期内将系统分为线性正速率、保持期和线性负速率,每个恒速阶段均可以平滑为正弦函数的一部分。
2.2 遗传算法控制器优化
本文采用的实数编码遗传算法,并对其进行优化,能够在系统重新初始化时达到理想的输出。该优化控制器被用于寻找多个参数np=16的最优设置,从而形成参数向量,即

其中,增益向量g由式(2)中PID增益构成,可表示为

tl为前置时间,用于式(9)和式(10)。图3中与黏滑间隔对应的线性电压变化阶段构成了一个区间矢量:
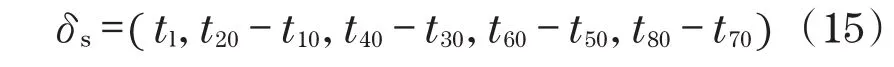
在式(9)和式(10)中,4个黏滑间隔和2个二次变化的线性电压速率共同构成速率向量为

此外,a2和a6是式(9)中前馈电压的2倍。
图4中的参数初始化模块的输入是参数向量{Pj}nc×1≡[pij]nc×np的 上 界bu≡(bui)1×np和下界bl≡(bli)1×np,以及在 0 和nb之间的初始随机整数nij,它们一起分别提供np参数和nc控制器:


图4 基于遗传算法的实验控制器优化Fig.4 Experimental controller optimization based on genetic algorithm
对所有控制器Cj使用LVDT测量结果yLVDT(Cj,t)作为输入轨迹yd(t)的跟踪结果,每个控制器的适应值fj和累积相对适应度Rj可被计算为
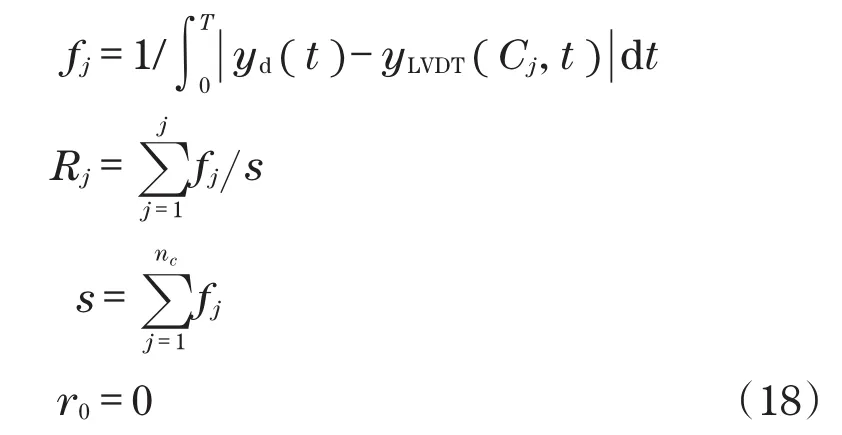
在图4中,描述了一个典型的相对适应度分布Rjvs.j,通过实时处理获取控制器nc的每一次迭代参数Pj,每次选择0~1之间的随机数nsj。研究中,P1=CK,Ns1的取值范围为rK-1<Ns1<rK。处理过程中较低适应度值的控制器被消除的概率明显更高。即具有较高适应度值的控制器在选择Pj的过程中更容易被选中和和具有更长的使用时间。由于一个特定的控制器有不止一次被选择的概率,所以在相对适应度分布中重复选择某个控制器所涵盖的累积跨度可能是最大的。这样的控制器在下一代中被作为控制器的次数最多。
将父控制器的所有参数向量执行遗传交叉和突变过程,生成子控制器集合Oj的参数向量。采用α=0.5的BLX-α交叉和非均匀突变。每次交叉执行np(nc/2)次,概率为πc,可以表示为两个子控制器在由一对父控制器的参数值形成的两个界之间随机选择参数为

式 中 :ak=max(pmnik-a(pmxik-pmnik),bli);bk=min(pmxik+a(pmxik-pmnik),bui);pmxik=pmxik=max(pip2k,pip2k-1);pmnik=min(pip2k,pip2k-1)。
如果以随机方式在0~1之间选择的数字概率大于πc,则不启用交叉,并且选择的参数对作为后代对被传递。如果启用了交叉,在0~nb之间的两个连续的随机数njk给出了变化后的参数为

在完成所有父对的交叉之后,每个后代都要进行变异操作,其概率为πm。如果允许突变来更改ng的参数,则通过在选择0~1之间的一个分数随机数f和0~1之间的另外随机数nm来设置子代参数值:

式中:ngm是由于收敛失败而停止优化的最大集合数。随着后代迭代次数的增加,式(21)可减少突变的影响。当累积适应度中的变化δ在约束ε内时,通过寻找上一代收敛到的具有最高适应度值的控制器,终止优化过程。
3 试验结果分析
3.1 正弦信号响应
设置安全阀工作压力为15 MPa,输入信号采用振幅20 mm、频率1 Hz的正弦信号,在已经提出的FPID控制器[9]和改进的基于GA优化的FPID控制器(FPIDGA)作用下,系统的响应输出如图5所示。可以看出,采用传统FPID控制方法存在较大的相位差,而优化后的FPIDGA使系统输出相移误差从45%降低到6%左右。
在表1和表2中对两个控制器参数进行了比较。表1中的第4个参数是由Sarkar等[9]得出的任意固定的提前时间。表1中的其他时间参数对应于滑动运动和黏滑运动4个时间点。事实上,表2中的所有模型估计参数都接近各自的优化值。虽然通过采用与跟踪频率不同的0.05 Hz正弦激励来获得参数,但基于此获得的静摩擦模型被认为是准确的。此外,表1和表2中给出了每个参数的上下界,参数上下界之间差距较大,表明参数边界的设置不需要精确的计算。

图5 基于遗传优化的FPID控制效果Fig.5 FPID control effect based on genetic optimization
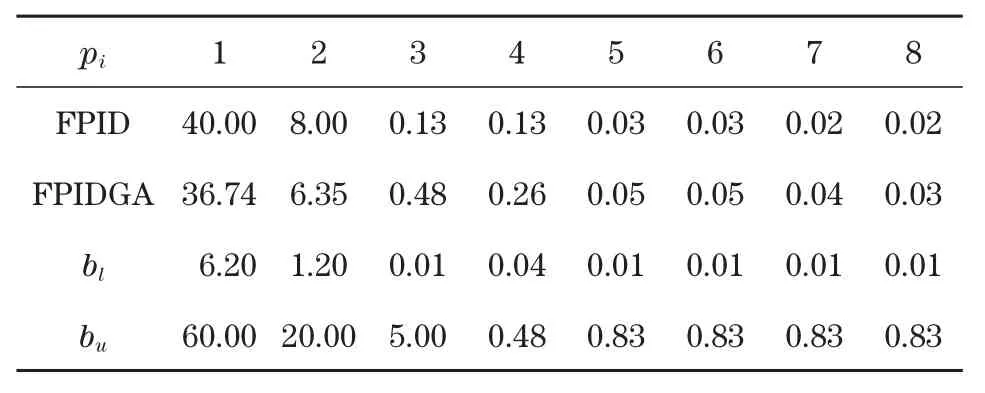
表1 遗传算法控制器增益和时间Tab.1 Genetic algorithm controller gain and time

表2 前馈控制器速率Tab.2 Feed forward controller rate
进一步,研究了系统在振幅20 mm、频率1 Hz正弦信号下的响应,并与Kim等[11]研究进行了对比,如图6所示。

图6 基于FPIDGA控制器气缸D正弦信号响应Fig.6 Cylinder D sine signal response based on FPIDGA controller
由图6可以看出:系统在第1个周期和第3个周期内误差保持在±1 mm之间,在第2周期,系统最大误差增加到2 mm。虽然气缸静摩擦力由于反向运动在500 N到-300 N之间发生了较大变化,但系统的控制效果较好。Kim等[11]研究了自适应反步控制器的控制性能。该系统由变转速伺服电机驱动液压系统,通过LVDT信号获得气缸的位置。该系统中,系统对1 Hz正弦信号的跟踪误差在-1~2 mm减小到±1 mm之内。对比分析可知,本文采用比例阀同样达到了相同的控制精度。
3.2 阶跃信号响应
在FPIDGA控制器作用下,气缸D对不同阶跃信号的响应如图7所示。在图7中,阶跃信号幅值分别为5,15,25 mm。可以看出:不同输入信号下,系统的上升和稳定时间存在明显差异,3种阶跃信号下系统稳定时间分别为0.60,0.68和0.70 s。Lee等[12]研究了伺服系统下气缸的阶跃信号响应,其在15和25 mm无负载下,系统在0.5 s内均实现了无超调跟踪。本文采用的为高摩擦力气缸,具有死区和低带宽的比例阀。对比响应结果可知,本文提出的遗传算法优化前馈控制器取得了类似伺服系统的控制性能。

图7 基于FPIDGA控制器气缸D不同阶跃信号响应Fig.7 Cylinder D different step signal response based on FPIDGA controller
4 结语
本文采用一种改进的遗传算法,优化了一种用于工程机械的电液系统实时串联前馈PID控制器参数。所设计的实数编码遗传算法不仅提供了一个高效的优化器,还提供了一个稳健的系统结构。该控制器除了易于优化,降低成本外,还可用于恶劣和尘土飞扬的工作环境中,并易于维护使用。对比优化后控制器的跟踪性能,尽管系统成本较低且具有高度非线性,但在阶跃信号和正弦信号作用下,均与高精度伺服系统的跟踪性能相当。

