基于极小子样的某列车齿轮箱箱体疲劳寿命可靠性评估

李永华，张 月，石姗姗

（大连交通大学机车车辆工程学院，辽宁大连116028）

在机械类产品中，进行样本量较大的试验往往比较昂贵，对产品进行跟踪也不容易获得大量的失效数据。基于极小子样的方法评估缺少试验数据的机械系统具有较好的准确性，因此，研究基于极小子样下的机械系统可靠性评估方法是当前解决小样本事件的有效途径之一［1］。

目前主要解决小样本数据的分析方法是数据样本扩充，比较常用的扩容方法有蒙特卡洛法［2-3］、支持向量机（Support Vector Machine，SVM）［4-5］和Bootstrap方法［6-7］。蒙特卡洛法原理简单，但在极小子样的可靠性评估中误差比较大［8］。SVM在小样本数据回归的处理上，能够利用现有样本拟合出较为理想的分布特征，克服了其他方法对样本容量需求大的问题，但其准确性对参数较为敏感，参数的优化过程较为繁琐［9］。Bootstrap方法很好地解决了试验样本量n≥10的小子样可靠性评估问题。但是对于样本量为n=1～3的极小子样可靠性评估，Bootstrap法也无能为力。且研究发现Bootstrap方法在扩展样本的过程中，再生样本数据会向均值集中，使得再生样本与原样本有较高的重复性［10］。

近年来，国内外学者在极小子样可靠性评估领域取得了很多研究成果。蒋喜等［11］提出了Bayes结合虚拟增广样本的分析方法，解决极小子样的可靠性评估问题。马宇鹏等［12］提出了Bootstrap-支持向量回归（SVR）-二阶累计量（SOC）方法框架和多阶矩虚拟样本容量扩充方法，解决小子样结构机构可靠性分析的问题。将Bootstrap与SVR方法结合，构建出结构机构可靠性极限状态函数，并利用SOC方法计算可靠度指标。该方法使用SOC方法进行计算虽然一定程度上减少了迭代次数，但其计算量还是远远大于Bootstrap方法。黄玮等［13］将虚拟增广样本法与Bootstrap方法相结合，解决了极小子样下使用Bootstrap方法进行评估结果不够准确的问题。但此方法中没有对Bootstrap方法抽样结果集中的问题给予妥善的解决。

本文提出一种基于齿轮箱箱体极小样本下的可靠性评估方法。针对Bootstrap方法的抽样过程存在的不足进行改进，并将虚拟增广样本评估方法和四分位差估计法与Bootstrap相结合用于极小子样下的齿轮箱箱体可靠性评估，其结果更接近于真实情况。

1 改进Bootstrap法求解性能分布函数

1.1 虚拟增广样本法基本原理

本文主要研究齿轮箱箱体可靠性评估问题，工程试验得出以下两条经验［14］：①机械零部件的疲劳寿命基本服从对数正态分布；②该部分总体的标准差大致为0.17。

目前对于小子样或极小子样的工程问题，并没有特别准确的评估方法。为了较为准确地对其进行评估，本文采用半经验方法来处理上述问题。

假设原始样本量n=2运用虚拟增广样本法增广至n=10。用参数表示的增广后的样本为［14］

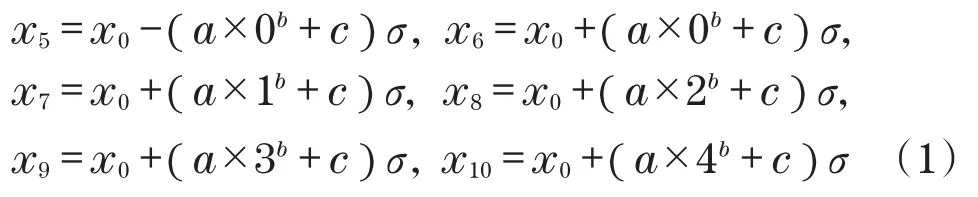
1.2 Bootstrap方法基本原理

Bootstrap方法是基于原始样本，并对其进行重抽样产生新的样本，根据新样本的分布形式判断总体的分布特征［15］。其基本原理描述如下：

设来自总体的原始样本分布为F(x)。样本x中的某一统计量为θ(F)（如期望、标准差等），

式中：θˆ(F)为θ(F)的估计；Tn为估计误差。

现从F(x)中重新抽样得到新的再生样本X∗=(，…，)，再生样本服从分布函数F∗(x)，实际上F∗(x)是F(x)的一个逼近，定义

利用的统计分析逼近Tn，重复上述抽样过程，得到每次的，根据式（2）和式（3）计算得到统计量的可能取值，将该值作为θ(F)的一个样本点，采用数理统计分析θ(F)的样本，求得θ(F)的估计值。

1.3 Bootstrap方法的改进与性能分布函数求解

为解决Bootstrap方法存在的不足，本文提出先对极小子样采用虚拟样本增广法将样本量由极小子样增广至小子样。再对小子样数据进行分组，然后分别对每组样本进行重抽样，克服再生样本过于集中的问题［16］。具体操作：将增广后小样本X=(x1，x2，…，xn)分为n组，每一组有n-1个样本，每个样本在增广样本的基础上删除掉第n-m+1项。如X1=(x1，x2，…，xn-1)，X2=(x1，x2，…，xn-2，xn)，…，Xm=(x1，x2，…，xn-m，xn-m+2，…，xn)，…，Xn=(x2，x3，…，xn)。

按照Fn(x)分布对各分组样本进行抽样。以X1为例，生成新的样本为=(，…，)，求得新样本的均值μ∗和标准差S∗，按照式如下公式分别求出均值、标准差的误差逼近值和，进而可求得性能参数的均值和标准差的估计值，即

对X1到Xn进行独立重复抽样后，可求得多组性能参数的μˆ和σˆ，取其平均值作为最终结果，并由此求得参数的分布函数。

1.4 四分位差估计法估计标准差

四分位差是上四分位数（Q3，即位于75%）与下四分位数（Q1，即位于25%）的差：

Wan等［17］提出利用四分位差来估计样本的标准差：

该方法不仅运用了次序统计量的重要性，也包含了样本量的信息，更为准确。

1.5 综合利用极大似然估计法和四分位差估计法

为进一步解决Bootstrap方法再生样本数据会向中间点集中的问题，提出一种综合估计方法。设某一样本数据X=(x1，x2，…，xn)，分别利用极大似然估计法、四分位差估计法估计出的标准差估计值σˆL与 σˆI，随后计算组合标准 σˆcom［17］：

最终将组合标准差σˆcom作为标准差σ的估计值。

2 极小样本下可靠性评估流程

基于极小子样的性能数据可靠性分析，其流程分为两个部分：一是对极小子样利用虚拟增广样本法增广；二是将增广后的样本运用改进的Bootstrap法进行可靠性评估。具体流程如图1所示。

3 齿轮箱箱体可靠性评估

对于在某线路上运行的城轨列车，其齿轮箱箱体分别在列车运行累计里程为63 369 km和20 145 km时，出现疲劳裂纹并开始渗油。根据此故障信息对该批次列车齿轮箱箱体进行可靠性的评估。

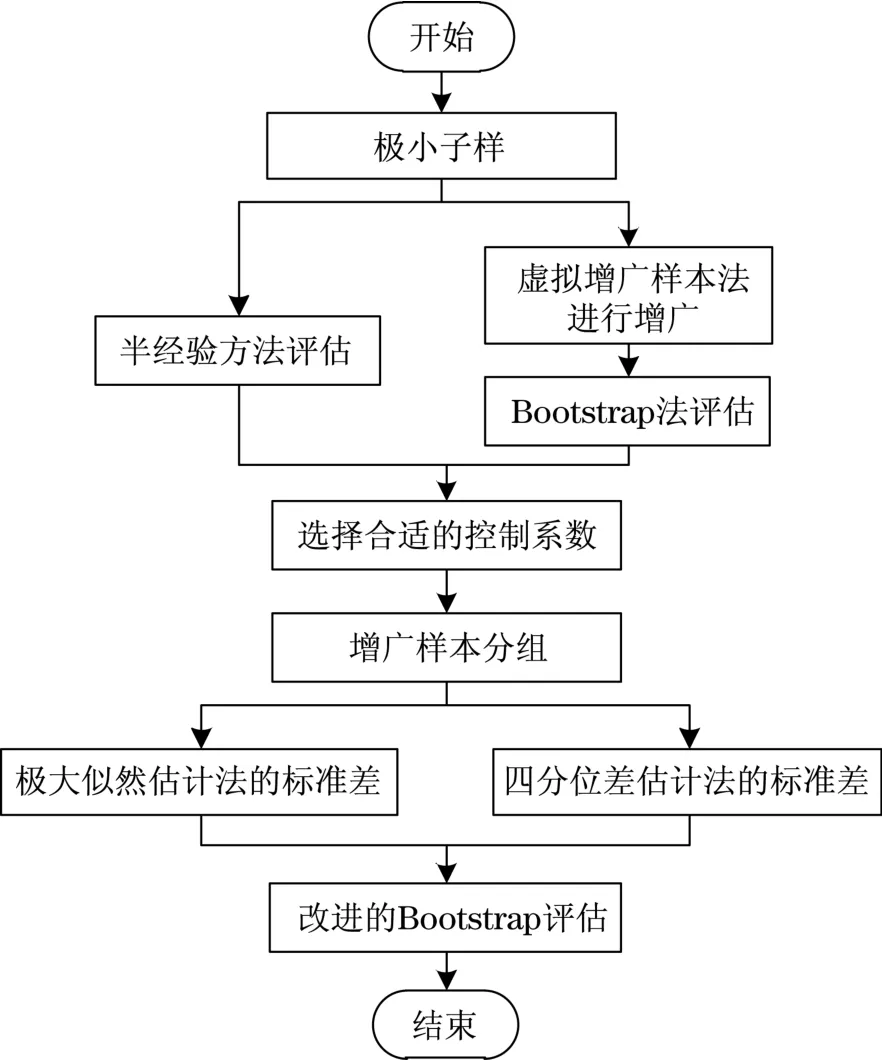
图1 改进的Bootstrap法可靠性评估流程Fig.1 Improved Bootstrap method reliability assessment flow chart

3.1 半经验方法评估

式中：Y1=lgS1=lg 63369=4.801877；Y2=lgS2=lg20145=4.304 167；α=0.05是给定的危险度。求解得Sˆlow(ban)=25049.9834。

3.2 虚拟增广样本法评估

将控制系数a，b，c按照1.1节所介绍的虚拟增广样本法进行增广控制系数的取值，如表1所示。增广结果如表2所示。

表1 控制系数取值Tab.1 Control coefficient value

表2 X的增广样本Tab.2 Augmented samples of X

将以上4组增广样本分别运用Bootstrap方法进行抽样，抽样次数N=10 000次，得到齿轮箱箱体的寿命均值和标准差的分布，b=4，a=0.007 8，c=0.017 5，这组控制系数的均值、标准差分布如图2和图3所示。

图2 未分组抽样均值的直方图分布Fig.2 Distribution histogram of ungrouped sample means

图3 未分组抽样标准差的直方图分布Fig.3 Distribution histogram of standard deviation of ungrouped sampling

将4组增广后样本用传统的Bootstrap方法评估结果与半经验法的评估结果相比，结果如表3所示。

由表3可知，b=4，a=0.007 8，c=0.017 5这组控制系数，是与半经验估计方法估计结果最相近的一组数据，故采用b=4，a=0.007 8，c=0.017 5这组控制系数进行改进的Bootstrap估计。

表3 4组控制系数取点结果比较Tab.3 Comparison of the results of 4 groups of control coefficients

3.3 利用改进的Bootstrap方法进行评估

将3.2节中得到的样本按照1.5节中介绍的分组方法进行分组，分为10组，具体分组结果如表4所示。对分组后的样本采用Bootstrap方法抽样，抽样次数N=10 000次，得到均值、标准差的分布如图4和图5所示。

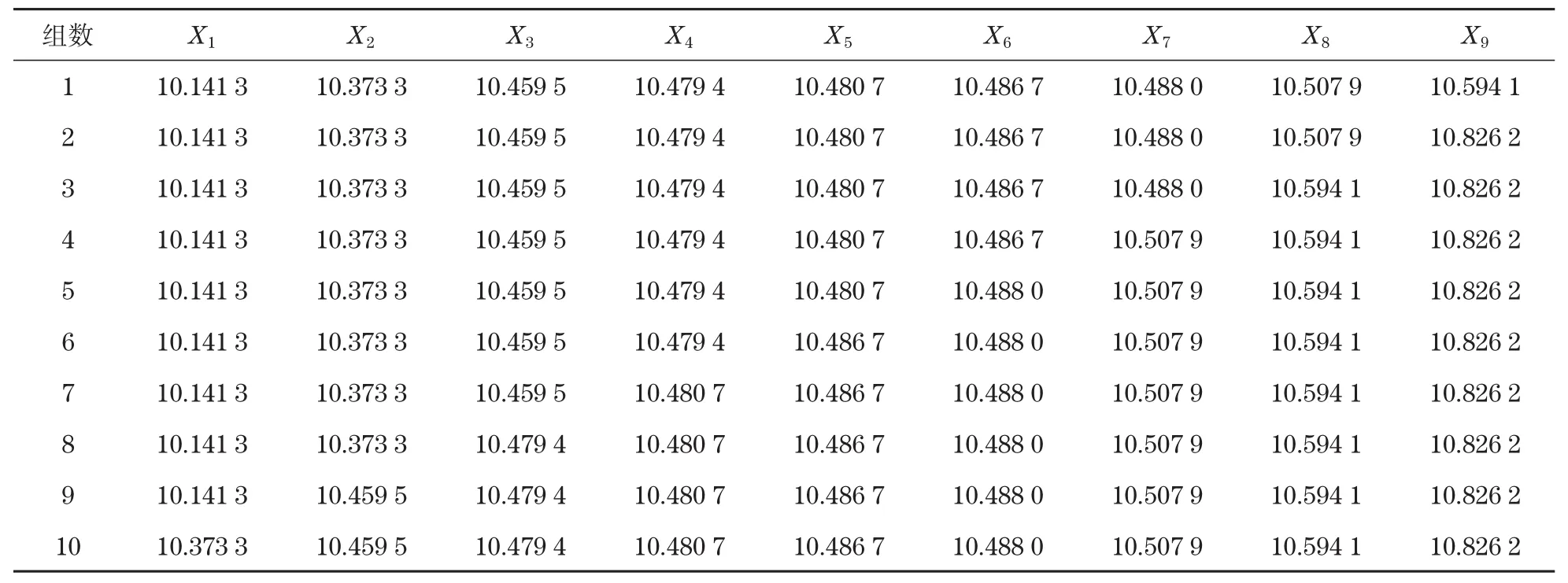
表4 改进的Bootstrap方法样本Tab.4 Samples of the improved Bootstrap method

利用正态分布图分别对Bootstrap方法和分组后的Bootstrap方法抽样获得的样本进行检验，均能够比较好地拟合样本的均值和标准差的分布。运用最大似然估计法分别将Bootstrap抽样方法得到的样本和分组后的Bootstrap抽样方法得到的样本进行估计，得到置信度为95%时样本的标准差估计值和均值的估计值。未分组、分组下的均值和方差的比较如表5所示。由表5可知，分组与未分组抽样下的极大似然估计法获得的均值的估计值差异较小。但样本分组抽样后的标准差估计值与未分组抽样时的标准差估计值相比略有改善。

图4 分组抽样均值的直方图分布Fig.4 Distribution histogram of grouped sample means

图5 分组抽样标准差的直方图分布Fig.5 Distribution histogram of standard deviation of group sampling

表5 未分组、分组下的均值和标准差的比较Tab.5 Comparison of mean and standard deviation under ungrouped and grouped samples

当b=4，a=0.007 8，c=0.017 5时未分组增广样本的四分位差估计法估计标准差的值为σˆI=0.1521。分组后样本的四分位差估计法估计标准差的值为σˆI=0.162。将最大似然估计法得到的标准差估计值与四分位差估计法得到的标准差估计值综合进行考虑，得到最终的标准差估计值，如表6所示。

利用改进的Bootstrap方法得到的标准差估计值，与未分组抽样下综合利用极大似然估计法和四分位差估计法得到的标准差估计值相比增大了1.44%，与传统的Bootstrap方法得到的标准差估计值相比增大了3.40%。这是由于分组后的样本相对分散，与四分位差估计法综合后进一步分散了样本的分布，更加符合齿轮箱箱体的疲劳寿命的分布。

齿轮箱箱体的疲劳寿命可靠度曲线如图6所示。

表6 Bootstrap方法改进前后均值和标准差的比较Tab.6Comparison of the mean and standard deviation of the improved Bootstrap method and the classic Bootstrap method

图6 齿轮箱箱体疲劳寿命可靠度曲线Fig.6 Gearbox case fatigue life reliability curve

由图6可知：行驶里程在约35 000 km前，改进的Bootstrap方法的可靠度评估结果比传统的Bootstrap方法的可靠度评估结果小；而在约35 000 km后，改进的Bootstrap方法的可靠度评估结果高于传统的Bootstrap方法的可靠度评估。

4 结论

本文运用虚拟增广样本法和四分位差估计法结合改进的Bootstrap方法，对某列车齿轮箱箱体的疲劳寿命进行可靠性评估，得出如下结论：

（1）通过分析指出了Bootstrap方法在极小子样评估问题中存在的不足，通过虚拟增广样本法对原始样本数据进行增广，使其能够符合Bootstrap方法的运用条件。

（2）运用改进后Bootstrap方法对增广后的样本进行可靠性评估，初步分散了齿轮箱箱体的疲劳寿命分布。综合利用改进的Bootstrap方法和四分位差估计法，进一步分散了齿轮箱箱体的疲劳寿命分布。本文方法对极小样本数据进行可靠性分析较传统方法更为合理。

（3）在可靠性分析中，仅考虑了齿轮箱箱体产生裂纹并渗油的失效模式，因此，计算结果仍存在一些误差，需要在后续的研究中进一步探索。