基于无超调算法的双步进电机伺服阀控制研究

孟淑丽，郝 雷

（1.北京经济管理职业学院工程技术学院，北京102602；2.河北大学电子信息工程学院，河北保定071002）

目前，国内外伺服阀采用永磁同步电机或步进电机作为电-机械转换器的设计较少，主要还是采用力矩电机或电磁铁等。永磁同步电机或步进电机作为电-机械转换器，具有抗干扰能力强、精度较高、无需进行D/A信号转换等优点，因此成为国内外液压控制学者研究的一个方向。

文献［1］采用三相混合式步进电机作为电-机械转换器，利用凸轮机构作为中间媒介，驱动阀芯轴向移动。实验表明，该方案响应速度快，精度好，稳定性好。文献［2-4］提出一种高集成直驱数字伺服阀，利用永磁同步电机，通过丝杠直接驱动阀芯运动，并采用角位移传感器闭环控制电机转角。该阀可实现高压力、大流量的控制，具有良好的静、动态性能。文献［5-6］提出一种插装式2D伺服阀，其电-机械转换器采用力矩电机，通过机械装置将电机衔铁与阀芯固连在一起，将控制器输入的电信号转换成衔铁的偏转，驱动阀芯旋转，结合伺服螺旋的原理实现轴向移动。位置传感器采用直线位移传感器，记录并反馈阀芯的直动位移，实现闭环控制。文献［7］提出了一种采用主备式驱动机构的双余度数字阀方案，其采用永磁同步电机作为电-机械转化器，采用滚珠丝杆及连接机构将电机输出的旋转运动转化为阀芯的平行移动，采用旋转变压器作为位置传感器构成回路闭环。实验表明：相比相同参数下的非余度数字阀，采用主备式驱动机构的双余度数字阀静态性能几乎没有变化，动态特性有一定下降；通过采用双同步电机主次架构可以提高数字阀的可靠性。

以上研究采用永磁同步电机或者单步进电机作为电液伺服阀电-机械转换器，存在瞬态响应慢、定位精度低的缺点，并且由于阀芯移动速度较慢，无法适应需要大流量的场合，也容易出现因油液污染导致的阀芯卡滞问题。对此，本文提出一种双步进电机驱动阀芯的新型电液伺服阀，并构建了双电机伺服控制系统，通过采用无超调算法对活塞杆运动过程进行控制，取得较好的控制效果。

1 新型电液伺服阀及系统构建

为了实现双步进电机分别控制的电-机械转换器，提出如图1所示的新型电液伺服阀结构，其中步进电机通过弹性联轴器与阀芯连接，阀芯末端与滚珠丝杠相连，滚珠丝杠在螺母中，螺母与步进电机轴螺纹连接，同时套在阀座上的轴承中。

利用图1所提出的新阀，构建单杆液压缸系统，系统硬件组成如图2所示。

图1 具有双步进电机的电液伺服阀Fig.1 Electro-hydraulic servo valve with double stepper motor

图2 电液伺服系统硬件组成图Fig.2 Hardware composition diagram of electrohydraulic servo system

系统主要由主控计算机、下位机、步进电机1控制器、步进电机2控制器、新型伺服阀、液压缸、载荷m和直线编码器组成。主控计算机装有Matlab/Simulink软件，实现控制程序编写与实现；下位机装有Advantech PCI 1716和PCI 1784数字输入输出（IO）卡，下位机通过IO卡分别与步进电机控制器、直线编码器进行通信；步进电机1控制器和步进电机2控制器分别控制伺服阀上的两个步进电机以及与其上的编码器进行通信；伺服阀与液压缸进出油口进行连接，控制活塞杆的伸缩；活塞杆上连接有负载m，直线编码器安装在测试台底座上，可感应记录负载的位置信息。电液伺服系统部分硬件参数如表1所示。

表1 电液伺服系统硬件参数表Tab.1 Hardware parameters of electro-hydraulic servo system

通过以上结构，两个步进电机的转动转化成阀芯的直线运动。当两个电机同向旋转时，则阀芯位移与角度差θ1-θ2成正比；当两个电机反向旋转时，则阀芯位移与角度和θ1+θ2成正比。即通过两个电机转动配合，阀芯可以适应不同场合的需要，既可以快速响应，也可以高精度慢速移动。

2 电液伺服系统动力学模型

基于图2，构建电液伺服系统动力学模型。模型基于以下假设：①4个边缘放大器零重叠，即活塞位移正比于阀的流量开口大小；②液压油物理特性稳定，且放大器输入的压力恒定；③管道压力损失很小，忽略不计；④液压缸系统刚度与管道载荷无关；⑤没有内泄和外泄。图3为所提出的电液伺服阀内部4个液压边缘放大器的示意图。

图3 液压滑阀放大器Fig.3 Hydraulic slide valve amplifier

高压源和阀芯左腔之间的流量Qa以及阀芯右腔和油箱之间的流量Qb表示为［8-9］

式中：p0为进油口压力；pa，pb为两个阀芯内腔压力；pT为油箱压力（0 Pa）；b为油口宽度；x为阀芯位移。

流量系数根据方程KQ=计算得到，其中孔口卸荷流量系数μ=0.5/0.7和流体密度ρ=780 kg/m3。

在一个脉冲步内，步进电机的动态行为可表示为［10-11］

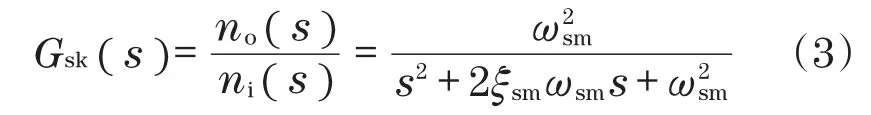
式中，ni，no为模型输入和输出信号（转子步）；ξsm为驱动阻尼比；ωsm为驱动器固有频率。

单活塞杆液压缸的动力学可表示为［12-13］

式中：A为油缸无杆端活塞横截面面积；a为油缸有杆端有效面积减少系数；E0为液体体积弹性模量；Va，Vb分别为油缸无杆端和有杆端的油液体积；m为活塞质量；FL为负载力；Ff为摩擦力。

液压缸内的摩擦力、质量m与滑动面间的摩擦力可以表示为一个与相对速度和Stribeck力、库仑力和黏性力之和相关的函数，它可用Tustin模型表示为

式中：fn为牛顿摩擦力系数；Fc为库仑摩擦力；Fp为静态摩擦力；vk为静态摩擦临界速度；kt1，kt2分别为活塞和活塞杆密封圈的摩擦力系数；压力差Δp=pa-pb。

3 控制系统

根据电液伺服系统动力学模型，构建电液伺服系统控制原理图，设计采用无超调算法实现对伺服阀进行控制。双独立步进电机驱动的电液伺服系统控制系统如图4所示。

根据图4，整个控制系统主要包括主控制回路和反馈回路，主控制回路中包含了双步进电机控制系统。图4中，ya表示液压缸预先设定的位置，作为整个控制系统的输入信号。步进电机控制器收到输入信号后，分别向两个步进电机输出转速信号n1和n2，控制液压阀推动活塞杆的运动，并通过直线编码器建立反馈控制，这里的反馈控制信号用yr表示。为了能够实现液压阀阀芯和活塞杆位置的精确控制，这里采用无超调控制算法来实现活塞位置和速度的精确控制。因此，活塞速度为

式中：tc为当前时刻；y（tc），y（tc-1）分别为当前步和上一步的位移；Tc为算法步长。

如果活塞匀速运动，则其将在t1时刻到达预定位置ya。到达预定位置的剩余时间为

图4 电液伺服系统控制图Fig.4 Control diagram of electro-hydraulic servo system

式中：ya为预定位置。

根据式（10）可得步进电机在时刻tc能够达到的最大步数nm为

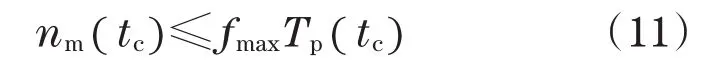
式中：fmax为步进电机最大频率。

根据阀套中阀口长度尺寸，考虑到阀芯的移动范围，在控制算法中引入最大步数nmax：

式中：xmax为阀芯最大位移；psm为丝杠每转对应步进数；pb为阀螺距。

4 仿真与实验分析

为了验证本文设计采用的无超调算法双步进电机驱动的电液伺服控制系统的性能，利用Matlab/Simulink软件，建立仿真模型，对比分析采用超调算法和未采用超调算法前后，双步进电机驱动的电液伺服阀活塞杆运动情况。设置驱动阻尼比、驱动器固有频率、步进电机最大频率和算法步长等仿真参数，如表2所示。

表2 仿真参数表Tab.2 The table of simulation parameter

设置输入信号为阶跃信号，未采用超调算法的伺服控制系统活塞位移响应如图5所示。从图5中可以看出，活塞位移设定值为15 mm，最大位移达到25 mm，超调量较大，这是由于该伺服系统采用双电机控制，在未采用超调算法时，双电机的协调性较差，在运行过程中，由双电机产生的误差进行了叠加，造成活塞位移偏差较大。此外，从图5可以看出，系统稳定时间ts约为0.7 s，说明系统瞬时响应性能较差。

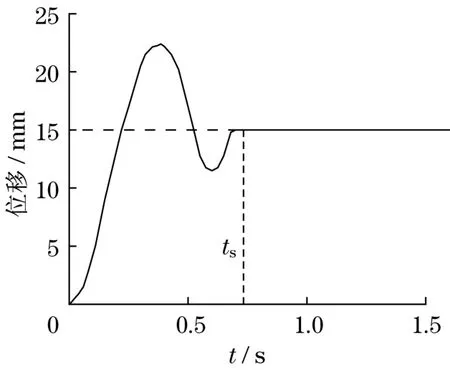
图5 未采用无超调算法的活塞位移响应（仿真）Fig.5 Piston displacement response without overshoot（simulation）

图6为采用超调算法的伺服控制系统活塞位移响应曲线。相比于图5，图6中的活塞杆的超调量大大减小，最大位移只有16 mm。系统稳定时间ts约为0.35 s，与图5相比减小了一半左右的稳定时间。说明采用超调算法后，双电机电液伺服系统的控制性能得到了较大的提升，主要表现在瞬态响应时间减小和控制精度得到提升。这是由于在无超调控制算法中，根据活塞速度和位置，对双电机的输出频率进行了综合调控，从而减小了双电机运行的误差，提高了活塞运动控制精度。仿真分析结果说明了本文所提的控制系统具有一定的控制效果。

为了进一步验证本文所提的无超调算法双步进电机伺服系统的性能，搭建实验平台，对采用无超调算法前后的活塞杆和阀芯的位移响应情况进行实验测试。为了能够与仿真实验进行有效的对比，这里活塞杆位移指令为15 mm。测试结果如图7和图8所示，分别表示采用无超调算法前后，双电机伺服控制系统的活塞杆位移响应状况。相比于图5和图6，图7和图8有一定的误差，这是由于仿真过程中对运行条件进行了假设，与实际过程存在有一定的偏差，但是总体变化趋势相对应，进一步证明了本文所提出无超调算法的双电机伺服控制系统的可行性。

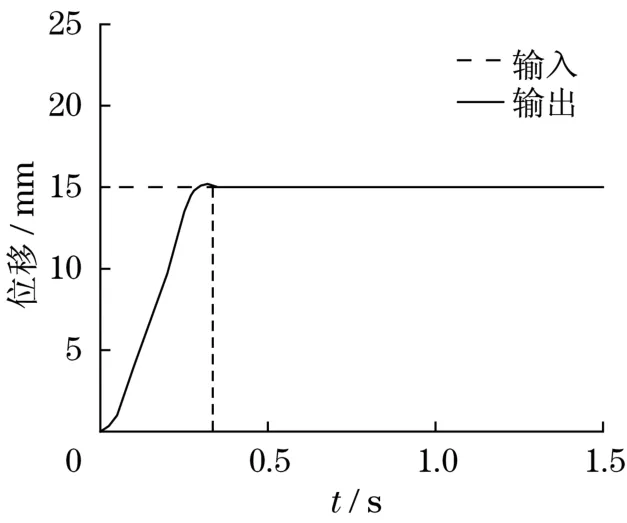
图6 采用无超调算法的活塞位移响应（仿真）Fig.6 Piston displacement response using no overshoot algorithm（simulation）

图7 未采用无超调算法的活塞位移响应（实验）Fig.7 Piston displacement response without overshoot（experiment）

图8 采用无超调算法的活塞位移响应（实验）Fig.8 Piston displacement response using no overshoot algorithm（experiment）

为了进一步说明无超调算法对双电机伺服控制系统的控制效果，对伺服阀阀芯的运动进行检测，得到如图9和图10所示的阀芯变动曲线，其中，纵坐标n表示脉冲步数。从图9中可以看出，在阶跃信号输入时，阀芯的位置发生剧烈的变化，相比于图9，图10中采用无超调算的阀芯位置变化幅度减小，说明当采用无超调算法后，阀芯位移被很好控制，并只往一个方向移动（脉冲步数值均大于0），有效地消除了超调量。此外，图9和图10阀芯的位置变化，与图7和图8活塞杆位移的变化相结合，进一步说明测试结果的正确性。

图9 未采用无超调算法的阀芯位置变动Fig.9 The change of spool position without no overshoot algorithm

图10 采用无超调算法的阀芯位置变动Fig.10 The change of spool position with no overshoot algorithm

从以上实验结果可以看出，采用无超调算法的双电机伺服控制系统相比于未采用超调算法的双电机伺服控制系统，能够有效地减小输出冲击，并获得更快的瞬态响应和更高的定位精度。仿真与实验结果相吻合，说明所建仿真模型的正确性，能够有效地帮助预测实验结果。

5 结论

本文提出了一种采用无超调算法控制的双步进电机电液伺服控制系统。通过构造电液伺服系统控制模型，在步进电机输入信号端进行位置反馈控制，推导了无超调算法控制方程。利用Matlab/Simulink进行仿真并进行实验验证。结果表明：提出的双步进电机电液伺服系统在无超调算法的控制下，可以有效地减小输出冲击，具有较快的瞬态响应和较高的定位精度，仿真结果与实验结果相吻合，说明本文提出的无超调算法控制的双电机电液伺服控制系统的正确性和可行性，为双步进电机伺服系统的控制提供了理论依据。