初中数学中学生一题多解能力的培养策略
孙慎榕
【摘 要】一题多解,主要是指针对同一问题,找寻不同的解题思路与规律,探究不同的解答方法。通过对学生一题多解的能力进行培养与锻炼,能有效提高其思维和解题能力。本文结合实际教学案例,探究如何在初中数学教学中培养学生的一题多解能力。
【关键词】初中数学;一题多解;培养
初中是学生能力与思维提升的重要时期。初中数学中的很多问题是具有多种解决方式的,但是在教学中,某些教师并不注重习题所具有的这一特点,通常会采用最简单的方式直接解决问题,并不找寻多种解题方式,造成了学生的思维定势。所以必须改善教学,在课堂中培养学生一题多解的能力。
1 激发学生的学习兴趣
激发学生学习的兴趣,指导其自主走进数学课堂,是提高其解题能力的第一步。一题多解,具有一定的繁琐性、复杂性,所以学生在初次接触时,难以保持解题兴趣,更难以坚持在较长的时间内探究问题,掌握方法。要想激发学生的学习兴趣,教师可采用创设情境的方式,从学生的生活出发,将问题放在生活情境中进行讲解,使问题更直观,从而使学生更轻松地解决问题。教师也可采用阶梯性问题的方式培养学生的学习兴趣。在教学中,可运用阶梯式的问题作为引导,从小问题出发,逐步引导学生解决各种问题,从而使其得到满足感与自豪感,并逐渐喜欢上数学。此外教师也要提供充足的空间与时间,让学生自主思考,实现能力与思维的锻炼[1]。
如在教学平均数这一知识时,教师可提出这样一个生活化的问题:小红在初中时期选择了住校,住在一间八人宿舍,在住校期间与宿舍里的其他七位舍友成了好朋友。学校组织了体检,在体检过程中小红与其他七位舍友都测了体重,分别为43kg、44kg、42kg、43kg、44kg、44kg、45kg、43kg,这时小红突然想探究一下她们整个宿舍的平均体重,以加深对舍友的了解。大家可以帮助一下她吗?教师在提出问题后,结合问题的背景直接将学生拉进生活中,让学生通过实际的生活背景进行探究。在学生探究的过程中,教师可直接指出这个问题多个求解方式。可结合小组合作探究的方式,让其在小组合作探究学习中,进行思维的碰撞。最后在小组合作后,教师让小组选出一位同学回答。之后教师带领所有学生一同总结,评价每一小组的解题方式。第一种为将小红和其室友的体重相加,得出总和,最后除以人数就可以得出平均体重。第二种为先设置一个较为基础的体重40kg,对其中每人距基础体重的重量进行计算,然后将超出的体重数相加,并除以人数,以确定好平均超出的质量,最后加上40kg得出平均重量。学生也会产生其他不同的思考方式,教师对于这些方式都应表示赞扬,以鼓励其继续思考。教师在讲解完两种方式后,可让学生对比两种方式,研究哪种方式更好用。很多学生会表示,第二种方式更简便,但是在平时做题中很难思考到这种方式,但是运用时会使整个习题更便于计算,具有计算量低、解题速度更快的特点。所以学生在之后的这类习题的练习中更愿意将第二种方式作为主要的解题方式。
2 提高学生对知识点的掌握
在一题多解方式中,不同解题方式所依靠的知识点是不同的,所以学生需要有扎实的知识储备。学生只有在掌握这些知识点后,才能在看到习题时,顺利产生解题思路。所以拓宽知识的层次,加深学生的记忆和理解,是教师教学的基本任务。在教学中,教师应结合一题多解的习题,深化学生对知识的理解和运用[2]。
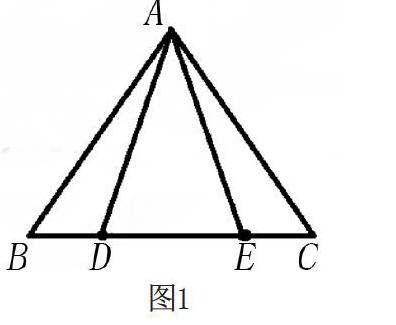
如在讲解过程中,找寻一个经典习题:已知一个三角形ABC,BC边上存在两点D、E,其中AB=AC、AD=AE,求证BD=CE。在提出问题后,教师应让学生自主思考,并进行小组合作学习,探究不同的解题方式,总结不同方式所采用的知识点。在小组合作学习结束后,教师应让每一小组发言,最后与学生一起归纳解题方式。这一问题主要有两种解决方式。第一种,是求证三角形全等。可以通过条件,建立起多组三角形之间的全等。通过边、角之间的关系,找到相等关系,并运用相关性质,得出三角形全等。这一方式较简单,大部分学生能想得到其所用的知识点是全等知识点。第二种,是用等腰三角形所具有的特点——等腰三角形具有三线合一的性质,解决问题。通过两个等腰三角形的高线是其中线这一条件,证明两个三角形的底线被中点平分,进而其长度相等。第二种解题方式只有小部分学生能想到。所以在课堂中,教师需要進一步的提醒。从这一习题也可以发现,不同解题方式所运用的知识点是不相同的,不具备扎实的基础知识就很难灵活运用相关的知识,进而难以想到其他解题方式。
3 培养学生的创新思维
要想一题多解,就需要具有一定的创新思维,需要根据习题,结合所学习的知识,寻找突破点。在一题多解习题的解答过程中,所有的思路并非是突发奇想产生的,而是基于基础知识,结合学生的创新思维产生的。并且一题多解习题也会大大提升学生的创新思维,锻炼其发散思维[3]。
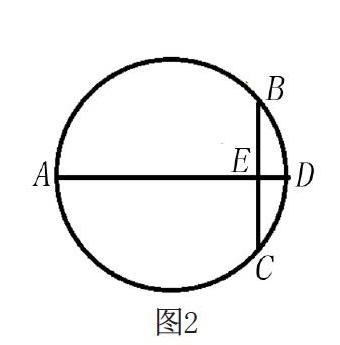
如在讲解习题“在圆中,其中AD为直径,BC为弦,其中AD⊥BC,其中交点为E,请问其中可以得出哪些结论”时,可让学生从不同的角度思考。由于问题具有开放性,所以学生在思考的过程中会发散思维,不会受到习题条件的限制,这对其能力的提升有重要作用。在这一习题中,学生很容易直接从线段与角度两个方向寻找其中的结论,并通过思维的发散,寻找到更多条件和结论,进而巩固所学知识。之后教师再引导其思考,从不同的角度思考问题,如引导学生思考勾股定理、弧等相关的知识。从这一习题可以发现,让学生从多个角度思考问题,对提升其思维能力与推断能力具有重要意义,能培养其创造性思维与一题多解的能力。
4 培养逆向、横纵向思维,提高解题能力
每一问题的解决都会使学生获得学习上的满足感,提升学习兴趣,希望提高数学知识的学习能力。为提高其解题质量与效率,要提高其思维能力,主要可以从逆向思维与横纵向思维进行培养,从而使其摆脱传统思维的束缚,有更多的方法解决问题。并且培养其逆向、横纵向思维,能使其打破思维定势,不再依靠单一的解题方法。
第一,逆向思维。逆向思维,与正常解题思维不同,是从反方向思考问题,进而找寻解题思路,最后解决问题。逆向思维的使用,主要是从问题的结论出发,分析其所需的条件,最后找出这些条件,解决问题。在培养逆向思维时,教师可以从数学公式、定理、命题入手,从简单的知识出发,进行思维的锻炼。
第二,横纵向思维。横纵向思维主要是在逆向思维基础上,进行更加宽广的、多个方向的思考。进行多个方向的思考,会有多个不同的立场,加上解答问题的效率与难度是不同的,所以取得的收获也是不相同的。如在创新思维的习题中,每一个思考方向所需运用的知识是不同的,所以取得的收获也就不同。在这一思维能力的培养中,教师既要发挥引导作用,又要给学生提供充足的时间与空间,避免喧宾夺主。
总之,初中数学教学中,注重学生一题多解能力的培养,能使学生在之后的数学学习中,具有更加灵活的思路和更强的能力。教师可在教学中结合情境教学、例题教学等方式,达到兴趣提升、逆向思维和横纵性思维锻炼、创新思维培养与夯实基础知识等目的,建立更高效的课堂。
【参考文献】
[1]赵正萍.初中数学例习题的教学策略研究[J].数学教学通讯,2019(32).
[2]张利平.在初中数学一题多解中培养学生数学思维的探讨[J].求知导刊,2019(32).
[3]顾定伟,李卫星.核心素养下的教学探微——从一题多解管窥初中数学教学[J].中学数学研究(华南师范大学版),2019(14).
[4]李娜.如何培养初中学生数学解题反思能力[N].太行日报,2019(7).

