坐标法在高中数学解题中的应用
唐再清

【摘 要】数学学科作为高中阶段的基础学科,对于学生理性思维能力和创造能力的培养有重要作用。新课程改革对高中数学的教学思路和教学方法提出了更高的要求。坐标法作为数形结合教学方法中的重要内容,可以有效深入学生对课本知识的理解与运用,所以高中数学教师应该重点关注这一方法。本文对坐标法在高中数学解题中的应用进行了深入的讨论研究。
【关键词】高中数学;坐标法;解题能力;应用探讨
对于高中数学而言,建立知识间的联系是解决数学问题的关键。通过坐标法将抽象的内容立体化,展现问题中的数量关系,能加深学生对知识的理解和分析,帮助学生迅速解题[1]。教师要在课堂上积极引导学生形成数学思维,灵活使用坐标法,促进学生深入思考,提高学生的数学解題水平。
1 以坐标法解决向量问题
向量问题具有代数和几何的双重特征,利用坐标法解决向量问题,既要考虑代数也要重视几何。根据题目中的条件在坐标中标明向量的方向和长度,能使向量间的关系更加清晰,更利于使用运算法则快速求解。教师在讲解向量问题时,要先多动手示范,以坐标表示向量,引导学生逐渐形成这种思维习惯;然后要让学生自己练习,把已知向量画在坐标系中,分析坐标系中暗含的等量关系,利用计算规则逐步得出答案。
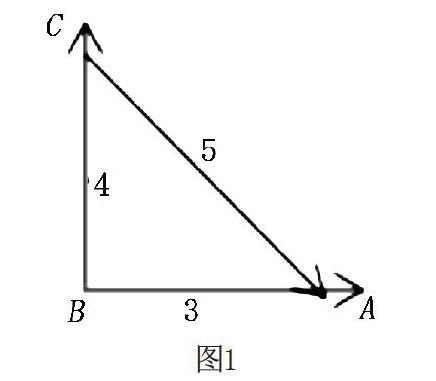
如在教学“平面向量”时,笔者设置了这样一道例题:已知平面上三点A、B、C满足、、,则的值等于多少?学生无法直接从题目中看出这些向量之间的关系,不能确定计算时向量的方向。于是笔者让学生先将这些向量在坐标图中表示出来,如图1所示。
学生根据坐标图理清了三个向量的位置以及数量关系。据此学生能准确计算了:因为、、,所以△ABC为直角三角形且∠ABC=90°,即AB⊥BC,所以。借助坐标图不仅能使复杂的数字关系具体化、生动化,而且能揭示出潜在的数量关系,进而以简便方法得到最终结果。
2 以坐标法解决函数问题
高中函数问题既是贯穿课本的重点,也是学生做题时的难点。借助函数图象解析函数,有助于将函数性质与具体问题结合,能促进学生对题目的理解和分析,使学生运用函数的变形和转换顺利解决问题。教师不仅要让学生掌握函数图象的各种性质,了解不同函数的图象及其特征,并熟练运用;还要引导学生一边在坐标系中画出函数图象,一边找出题目中的隐藏信息,再根据题目的要求变化图象,获得解题方法[2]。
如在学习“函数的应用”时,学生遇到了一道难题:已知函数在有最大值2,求的值。学生不明白函数最大值与之间的关系,笔者提示道:“大家想一想之前学习时提到的函数的性质,函数的最大值与什么有关?最大值又与定义域有什么关系?”学生立刻意识到这个函数二次项系数为负,所以图象开口朝下,先增后减,而条件限定了定义域,如果在定义域上为增函数,那么在最大时最大;如果在定义域上为减函数,那么在最小时最大;如果定义域在函数对称轴两侧,那么在函数顶点处达到最大,所以决定性的因素是限定的定义域在对称轴的哪一侧。教师可以引导学生借助图象探讨对称轴与给定条件间的关系,以此使学生的思维更加敏捷,解题准确率更高。
3 以坐标法解决几何问题
几何问题主要考查学生的空间想象能力。但是由于学生普遍存在缺乏经验、想象力水平低的问题,所以教师需要借用三维坐标将几何体的点、线、面有机组合,让学生通过明确的标识认识几何体,构建空间图形。一方面,要让学生根据几何图形理清线段间的数量关系和位置关系,并在大脑中初步建立印象;另一方面,要让学生学会使用辅助线、辅助面等捕捉新的关系,搭建桥梁,达到目的。
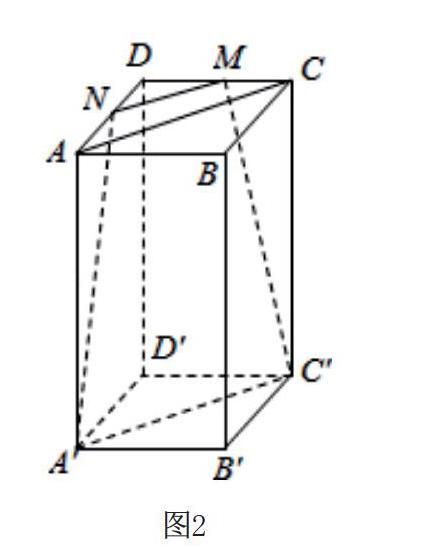
如在学习“空间几何体”时,笔者列出了一道例题:如图2,ABCD﹣A′B′C′D′为长方体,底面是边长为的正方形,M、N分别是CD和AD的中点,判断四边形MNA′C′的形状。
当学生不知从何入手时,笔者提醒学生:从长方体的底面是正方形可以联想到正方形的什么性质,从中点又能联系到什么知识点?如何将两者结合?学生在认真思考后有了一定想法:根据三角形的中位线定理和正方形的性质可得MN//A′C′//AC,且MN=A′C′=AC,进而可判断四边形MNA′C′的形状。于是写道:∵ABCD﹣A′B′C′D′为长方体,底面是边长为的正方形,M、N分别是CD和AD的中点。∴AC=,MN∥A′C′∥AC,且MN=A′C′=AC,故四边形MNA′C′为梯形。解几何问题时构建坐标图是必不可少的,这样有利于学生推理和证明,也有利于培养学生的空间想象力。
总之,利用坐标解决数学问题不失为一种效果显著的方法,利用坐标法能将数字问题转化为图形问题,使零散的问题系统化、立体化,有利于提高解题效率。教师要结合学生的实际情况,借鉴科学方法提高教学质量,培育学生的数学素养。
【参考文献】
[1]赵奕.坐标法在高中数学解题中的应用探析[J].新一代:理论版,2018(19).
[2]江志海.浅谈高中数学坐标法的解题研究分析[J].考试周刊,2019(9).

