保持Ricci孤立子结构的共形变换*

吴元芬, 郭震, 何雅

(云南师范大学 数学学院,云南 昆明 650500)

1 引 言

设(Mn,g)为一个完备的n维黎曼流形,如果存在Mn上的光滑向量场ν,使得

(1)

其中Ric是度量g的Ricci曲率张量,Lνg是黎曼度量g沿着方向ν的Lie-导数,λ为给定常数,则称M为Ricci孤立子.特别地,当ν是梯度向量场,即存在Mn上以ν为梯度的势函数f,(1)变为

Ric+Hess(f)=λg

(2)

其中Hess(f)是f的Hessian,则称M为梯度Ricci孤立子,f称为Ricci势函数,当常数λ分别满足λ<0,λ=0,λ>0时,分别称Mn为膨胀的,稳定的,收缩的.特别地,当函数f为常数,则称Mn为平凡的Ricci孤立子,此时Mn是Einstein流形；反之,若Mn是Einstein流形,则f为常数,即Mn为平凡的.

Ricci孤立子作为Ricci流的自相似解,是几何及分析的重要研究对象,受到数学家的关注[1-5].本文研究保持Ricci孤立子结构的共形变换,证明了2维梯度Ricci孤立子的共形刚性定理,给出了在维数大于2的情况下，保持梯度Ricci孤立子结构的共形变换必须满足的条件.

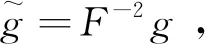
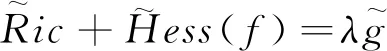
(3)

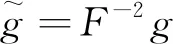
(a)如果λ≤0,该共形变换是等距变换；

(b)如果λ>0,则minF≤1≤maxF,且等号成立的充分必要条件是该变换是等距变换.

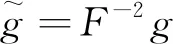
Ric(F,F)+〈ΔF,F〉

(4)

2 准备工作

利用外微分和活动标架法给出共形变换下一些基本量的变换公式及梯度Ricci孤立子的基本方程.为了简便,采用Einstein求和法(重复指标为求和指标),规定指标范围:1≤i,j,k,t,…≤n.设(Mn,g)是一个黎曼流形,且n≥2,在Mn中选取局部标准正交标架场{ei}，{θi}为{ei}的对偶标架场.则Mn的结构方程为

其中d为外微分算子,θij,Rijkt为黎曼度量g诱导的联络形式与黎曼曲率.Ricci曲率与纯量曲率R分别为Rij=ΣkRikjk,R=ΣiRii.

设f∈C(M),有df=fiθi,其中fi=ei(f),定义函数f的协变导数：

fi,jθj=dfi+fjθji

fi,jkθk=dfi,j+fi,kθkj+fk,jθki

则

fi,j=fj,i,fi,jk-fi,kj=ftRtijk

(5)

其中(5)的第二式是光滑函数f的Ricci恒等式.f的梯度向量场f,Hessian和Laplacian分别为

f=fiei,Hess(f)=fi,jθi⊗θj,Δf=fi,i

(6)

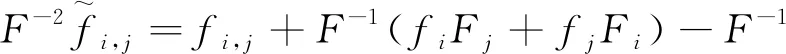
(7)

若(Mn,g)为满足(2)的一个梯度Ricci孤立子,则(2)可改写为

Rij+fi,j=λδij

(8)

容易得到

R+Δf=nλ

3 定理的证明

先证如下引理:

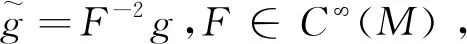
(9)

和

2(n-1)ΔF-n(n-1)F-1|F|2-(n-2)〈f,F〉=nλF-1(1-F2)

(10)

证明在一个标准正交基下(3)变为

(11)

将(6),(7),(8)代入(11)得

(n-2)Fi,j+(fiFj+fjFi)-[(n-1)F-1|F|2-ΔF+〈f,F〉]δij=λF-1(1-F2)δij

(12)

对(12)进行i=j收缩有(10),将(10)代入(12)即可得(9).

3.1 定理1的证明

证明(a) 因为n=2时,(9)和(10)简化为

-(fiFj+fjFi)+〈f,F〉δij=0

(13)

和

ΔF-F-1|F|2=λF-1(1-F2)

(14)

若M2紧,则F一定有最大最小值,在最大最小值点处|F|=0.又因为λ≤0,所以由(14)有

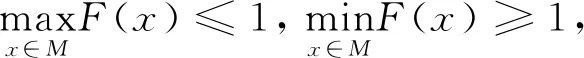
导致F|M=1.

(b) 因为

(15)

把(14)代入(15)有

ΔlogF=λF-2(1-F2)

对上式两边同时积分,因为λ>0,所以

因此maxF≥1,同理可得minF≤1.下证等号成立的条件

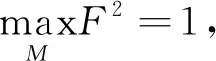
(16)

且

(17)

由(16)和(17)有

F-2(F2-maxF2)=0

则

F2=maxF2=1

同理有F2=minF2=1.

综上所述，定理1得证.

3.2 定理2的证明

证明从(9)开始,令

(18)

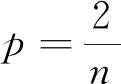
(19)

则(9)变为

(n-2)Fi,j=-fiFj-fjFi+pδij

(20)

由(20),则

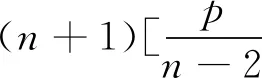
(21)

另一方面,由Ricci恒等式有

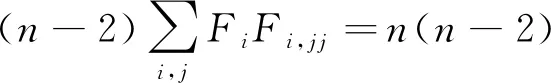
(22)

由(21),(22)以及(8),(18),(19)推出

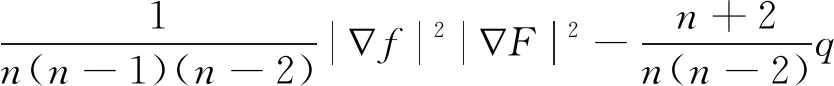
(23)

对(9)两边同时平方有

(24)

把(10),(24)代入(23)中消去含f的项,即可得到(4),定理2得证.