一个组合恒等式的若干组合描述*
邓伟升, 王守峰
(云南师范大学 数学学院, 云南 昆明 650500)
1 引 言
在组合数学中,表示组合数之间的关系的恒等式称为组合恒等式.Riordan在其著作中第一次系统地介绍了组合恒等式及其相关理论[1],Gould在《Combinatorial Identities》[2]中收录了500多个组合恒等式,到目前为止已知的组合恒等式不下千个.组合恒等式的证明是组合数学中的一个重要和活跃的研究课题之一,其证明方法多种多样[3-6],如利用组合数的定义和基本性质、数学归纳法、组合分析法、母函数法[7]、分类覆盖法[8]、概率法[9]、微积分法[10]、递推关系法等.
本文利用组合分析法、挡板法及母函数法等证明了组合恒等式
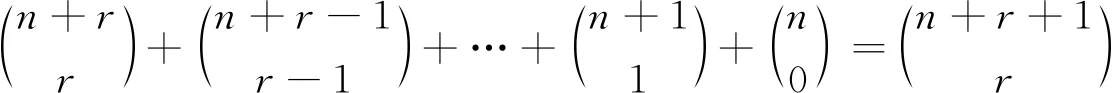
2 证明方法
2.1 组合分析法
组合分析法是证明组合恒等式的一种重要的方法,其思想是构造一个组合计数问题模型,先指出组合恒等式的一边是此组合计数问题的解,然后利用基本的计数原理来证明组合恒等式的另一边也是该组合计数问题的解.
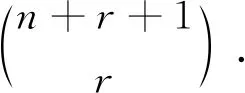
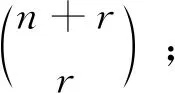
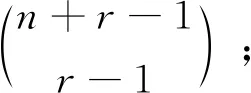
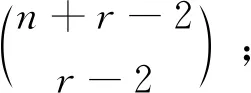
…
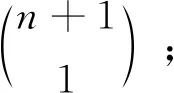
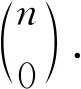
由加法原理可得
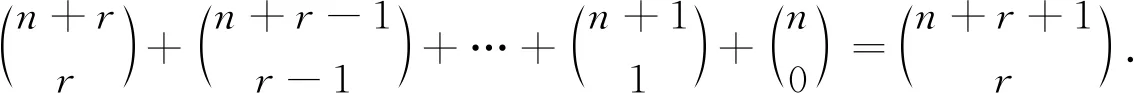
2.2 挡板法
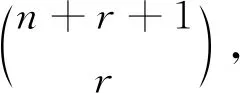

图1 n+r个小球和n+r+1个位置*
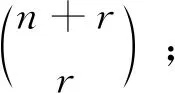
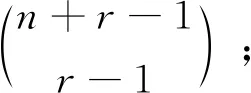
…
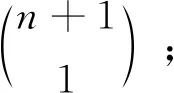
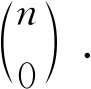
由加法原理,可得
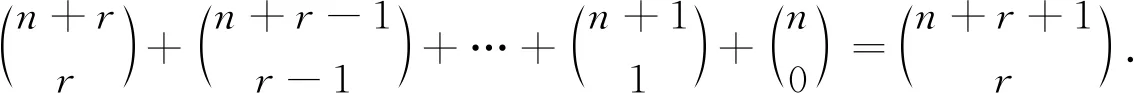
2.3 母函数法
母函数又称为生成函数,它是求解组合计数问题的一种重要工具,其思想是借助于幂级数的求和形式,而不考虑幂级数的敛散性来解决相关的组合计数问题.
构造生成函数模型:设A={a1,a2,…,an+r+2}是一个n+r+2元集,则A的r可重复组合数为母函数F(x)=(1+x+x2+…)n+2的展开式中xr的系数,而
又
F(x)=(1+x+x2+…)n+2=(1+x+x2+…)(1+x+x2+…)n+1=
比较左右两边xr的系数,可得
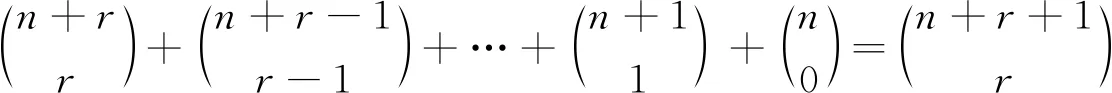
2.4 利用不定方程的非负整数解的个数来进行证明
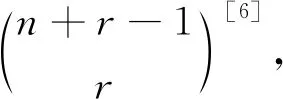
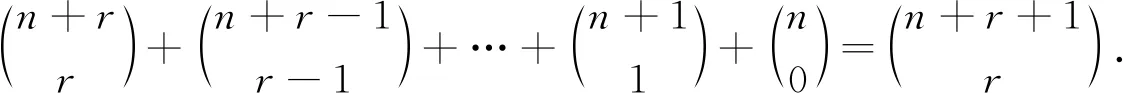
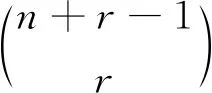
2.5 利用多重集的组合意义

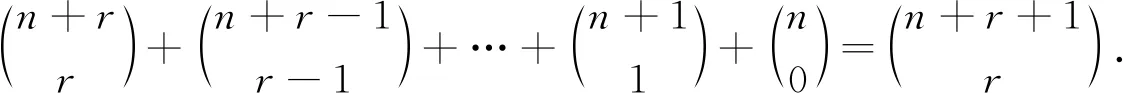
2.6 路径法
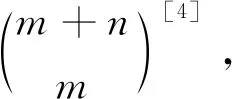
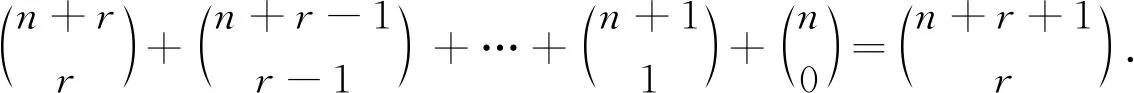
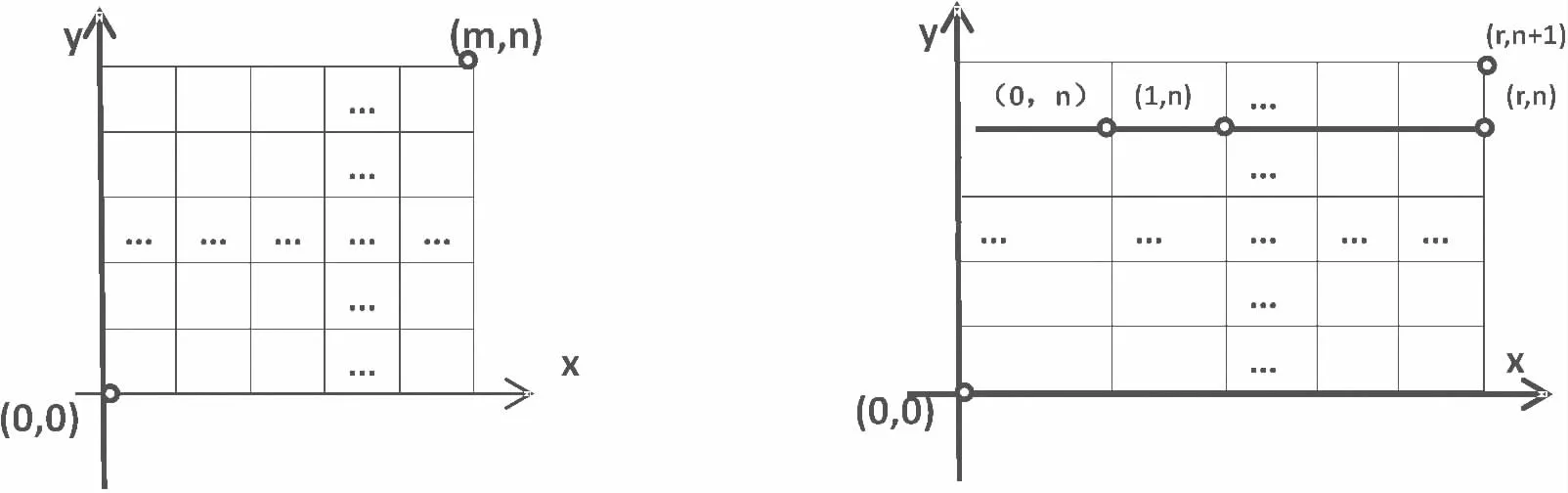
图2 从(0,0)点到(m,n)点的路径 图3 从(0,0)点到(r,n+1)点的路径
3 小 结
利用组合分析法、挡板法、母函数法、不定方程的非负整数解的个数、多重集的组合意义及路径法给出了组合恒等式
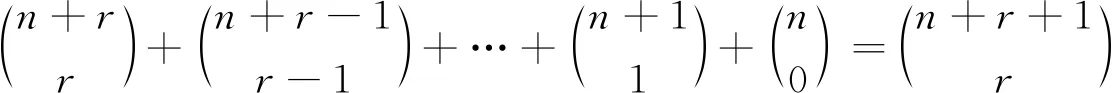
的组合描述,这些方法直观、富有启发性,对提高数学思维能力以及理解和掌握组合恒等式的证明具有一定的帮助.

