基于疲劳驱动力能量损伤参数修正的非线性疲劳寿命预测

薛齐文，许 旭，王生武

(1.大连交通大学 土木工程学院，辽宁 大连 116028;2.大连理工大学 工业装备结构分析重点实验室，辽宁 大连 116023)

疲劳破坏是轨道车辆中焊接结构常见的一种失效形式，这些焊接结构通常的承载状态是承受循环载荷作用，且往往承受变幅载荷作用[1]。对于轨道车辆结构，急需更为合理且实用的疲劳寿命分析模型，以有效解决车辆焊接结构的疲劳问题，避免重大灾害或安全事故，具有十分重要的工程应用研究价值[2-3]。

针对焊接结构疲劳问题，最为常用的疲劳寿命分析模型是线性的Miner法则，计算模型简单且便于工程应用。但该模型的损伤累积规则简化了疲劳失效的过程机理，使疲劳寿命的估计具有不确定性，易出现较大的偏差。大量的工程实际数据也表明，对于复杂的载荷加载，Miner法则的分析结果不准确，与实际结果偏差较大，常不能满足工程要求。对于多级变幅载荷作用时，加载历史效应不能忽略，因载荷加载次序、载荷间的干涉以及实时的疲劳损伤程度等相关因素对损伤累积有显著影响[4-5]。对于实际中普遍存在的变幅载荷作用下疲劳问题，迫切需要建立有效的模型处理变幅载荷下损伤累积过程，从而更好地预测疲劳寿命。

疲劳损伤从本质上分析是一个不可逆、材料性能退化和能量耗散的过程，可通过评估机械性能或物理性能的变化进行判定。非线性损伤累积理论是当前进行疲劳分析的2大类方法之一，所涉及的理论模型有损伤曲线、连续损伤力学、能量法、物理性能退化等模型[6]。虽然这些模型在一定程度上能处理载荷加载历史效应，但是其数学形式多为多层嵌套，计算形式复杂，有的还需引入额外的参数，难以直接应用于工程实际[7-8]。如何合理地描述复杂的载荷加载历史效应，进而构建准确的疲劳寿命预测模型，一直是工程专家迫切需要解决的实际问题。

近年来，部分学者将应变能密度参数用于跟踪损伤累积行为，提出了一种有效的疲劳寿命预测方法，且得到较好的应用[9-10]。文献[11]结合应变能密度参数，提出了疲劳驱动力能量的概念，建立了适用于高周疲劳状态下疲劳损伤累积的非线性损伤模型，可用于变幅载荷下疲劳寿命的预测，同时还引入应力比函数，探讨了载荷相互作用的影响。但在变幅载荷作用下，疲劳损伤累积规律因载荷幅值的变化而变得非常复杂[12-13]。疲劳损伤累积规律与加载历程密切相关，载荷加载次序、载荷间的干涉、疲劳损伤程度等因素直接影响着疲劳损伤累积规律，相关研究还需进一步深入探讨。

本文基于疲劳驱动力能量损伤参数，利用变幅载荷应力比、载荷循环比和实时疲劳损伤程度构建指数函数，对相邻载荷间的交互因子进行修正，建立改进的非线性疲劳寿命预测模型。所构建的疲劳寿命预测模型有效性和可行性通过不同材料的焊接结构在多级变幅载荷作用下的疲劳试验数据结果给予验证，并与其他数值模型进行对比。

1 基于疲劳驱动力能量的疲劳损伤累积

对于高周疲劳问题，疲劳寿命与应力之间的S—N曲线关系常用Basquin公式描述，即

(1)

式中：C为材料固有的疲劳强度常数；b为对应的材料性能参数，为常数；σ为载荷作用下的应力,常用应力幅表示；Nf为相应应力幅对应的疲劳寿命。

由于往复作用的外部载荷是产生疲劳损伤的主要因素，可按式(2)定义疲劳驱动力参数[14]，该参数与载荷循环数、应力幅以及对应的疲劳寿命直接相关。

(2)

式中：σD为疲劳驱动力参数；n为循环载荷作用的次数。

式(2)定义的参数是与实际载荷循环相关的增量函数,具有非线性特征。

关于高周疲劳问题，可忽略不计很小的塑性应变，依据式(2)定义的疲劳驱动力参数以及能量准则，可进一步定义疲劳驱动力能量参数，并将其简化为

(3)

式中：E为弹性模量；WDn为与n次循环载荷作用对应的疲劳驱动力能量。

式(3)定义的疲劳驱动力能量随着循环载荷的作用而不断变化，不断地循环累积，最终达到临界阈值。

损伤参数的确定是寻找疲劳损伤累积规律的一个关键问题。结合损伤累积理论以及基于能量耗散考虑，损伤参数D可采用疲劳驱动力能量的增量进行描述，为

(4)

式中：ΔWDn,D0为实际加载状态下耗散的能量；ΔWDc,D0为失效状态下耗散的总能量。

式(4)定义的损伤参数D直接与载荷循环次数相关，且两者之间为非线性关系。以损伤参数D定义的疲劳寿命预测模型则属于非线性疲劳寿命预测模型的范畴。预测模型中载荷与损伤是不可分离的量，在一定程度上可以体现载荷顺序效应。

依据式(4)定义的损伤参数，对于多级载荷作用，可通过迭代计算，得到第i级载荷作用下应力幅对应的疲劳寿命预测计算公式为[15]

(5)

其中，

式中：ni为第i级载荷作用下应力幅对应的循环次数；Nfi为第i级载荷单独作用下应力幅对应的疲劳寿命；Nni为第i级载荷作用下应力幅对应的循环次数比；下标p表示对应级别载荷根据预测模型计算得到的预测值。

在利用上述给定的模型、即按式(5)进行疲劳寿命预测时，只需要确定b和Nf这2个基本参数即可，而这2个参数可由试验所得的S—N曲线拟合确定，不需要引入其他参数，计算模式相对明显且直接，具有很好的工程应用性。

2 改进的非线性预测模型

对于恒幅载荷作用，疲劳损伤累积规律相对简单，累积规律比较容易探究。而在变幅载荷作用下，疲劳损伤累积规律因载荷幅值的变化而变得复杂。变幅载荷作用下的疲劳损伤累积规律与加载历程密切相关，载荷大小次序、载荷间的干涉、疲劳损伤程度等因素直接影响着损伤累积规律。

部分学者研究表明，载荷间的影响可用相邻两级载荷大小的比值进行描述，比值的大小直接决定交互影响的程度。在多级载荷作用下，利用相邻两级载荷应力比进行修正，对应的疲劳寿命预测模型为

(6)

其中，

式中：σi为第i级载荷对应的应力幅。

式(6)所示预测模型虽然有一定的改进，数值验证结果也有一定的提升，但是该模型仅考虑了载荷先后作用顺序的影响，而未能考虑高低载荷先后作用下实时疲劳损伤对疲劳寿命的影响，损伤累积的演化规律尚需进一步探讨。在变幅载荷作用下，破坏时对应的疲劳损伤累积往往不等于1，前期的低应力具有初始锻炼效应，而前期的高应力则使裂纹提前形成。如果直接仅用应力比表示载荷交互作用的影响，那么实际低应力的锻炼程度以及高应力裂纹的形成状态未能予以体现；可在交互因子中引入载荷循环比，体现载荷循环的作用程度。

按照疲劳损伤等效原理，损伤参数与循环比分数n/Nf的关系均可用幂函数的形式表示。对于多级载荷作用，疲劳寿命对应的循环载荷比分数可以经下式推导求得。

(F((Nni-1)e,σi-1))ωi-2,i-1=

(F(1-Nni,σi))ωi-1,i

(7)

式中：F为描述疲劳损伤状态的函数；ωi-1,i为第i-1级与第i级载荷间的交互因子；(Nni-1)e为前i-1级载荷作用下的等效循环次数比。

在式(7)对应的疲劳损伤模型中，体现载荷变幅影响的关键参数为交互因子ω。先高后低变幅加载时ω大于1，反之则ω小于1。在疲劳寿命等效模型中同时考虑载荷大小、加载次序以及载荷间的干涉影响，对应的疲劳寿命预测模型可统一写为

(8)

其中，

γ=ωi-1,i-2ωi-1,i

据上述分析，交互因子的定义是疲劳寿命预测模型的关键，如果将交互因子仅定义为相邻载荷的应力比，式(8)则与式(6)相同。在保证交互因子取值特征的同时，可进一步将相邻两级载荷作用的交互因子定义为应力幅比、载荷循环比或实时损伤相关的函数，即

(9)

式中：αi-1为与载荷循环比以及实时损伤相关的参数。

由上文推导可知，损伤参数可用驱动力能量的变化定义，且该参数与载荷循环比密切相关。据此分析，可以采用下面的2种形式对交互因子的指数参数进行定义，对交互因子进行修正，具体如下。

方法1：将交互因子的指数参数定义为与载荷循环次数比ni/Nfi相关的函数，为

(10)

将式(10)代入式(9),可得到按照方法1修正的疲劳寿命预测模型的交互因子为

(11)

(12)

方法2：将交互因子的指数参数定义为实时疲劳损伤Di的指数函数，为

αi=expDi

(13)

式(13)中损伤参数含有载荷循环比值，可将其代入式(9),可得到按照方法2修正的疲劳寿命预测模型的交互因子为

(14)

(15)

在疲劳寿命预测分析时，结合式(8)、式(10)和式(13)进行计算。式(10)和(13)分别代表2种改进的疲劳寿命预测模型的指数参数，模型中既有前后2级载荷的应力幅比，也含有载荷循环比或实时损伤量，能够有效地体现载荷次序的影响、载荷间的干涉以及实时疲劳损伤影响程度。此外，模型中仅含有常用的2个基本参数，通过试验数据比较容易确定，不需要引入其它多余的参量，方便应用于实际结构的疲劳寿命分析。

3 数值算例

为验证所提模型预测结果的可行性和有效性，依据文献中2种常用材料的焊接结构多级载荷加载的试验数据，将所建疲劳寿命预测模型与文献中模型的结果进行对比。

算例1：Q235B焊接接头疲劳寿命预测

Q235B是车辆转向架焊接构架的常用焊接材料，依据文献[12]中不同焊接形式在多级变幅载荷作用下的试验数据验证所建模型的疲劳寿命预测能力。对于不同级数的变幅载荷作用，采用不同分析模型得到的疲劳寿命预测结果见表1—表3,疲劳寿命预测结果与试验结果的对比如图1所示。表中，加载模式是指多级递增应力幅载荷作用时所对应的应力幅值。

由表1—表3和图1可知：对于Q235B焊接接头，在多级递增应力幅载荷作用下，文中所建非线性模型均能有效地进行疲劳寿命预测；相比较于其他模型，所改进模型预测结果更符合于试验数据。依据不同方式交互因子修正的对比结果，可以看到实时损伤修正模式更为合理。

算例2：铝合金焊接接头疲劳寿命预测

铝合金材料是轨道交通领域常用的焊接接头材料，以文献[15]中铝合金试件在多级应力幅载荷作用下的疲劳试验数据验证本文预测模型的疲劳寿命预测能力。多级应力幅试验加载包括由高到低、由低到高以及随机加载3种情况，所对应载荷的应力幅σi分别为305，280，260和240 MPa这4个等级，各级应力幅值对应的单级应力幅疲劳寿命Nfi分别为38 000，87 612，180 660和394 765次。不同预测模型所对应最后一级载荷的疲劳损伤以及疲劳寿命预测结果见表4，疲劳损伤累积结果的对比如图2所示。

由表4和图2可知：对于铝合金焊接接头，在递增、递减以及随机3种类型的变幅载荷作用下，文中改进的非线性疲劳寿命预测模型均能对该焊接接头的疲劳寿命进行有效的预测；与传统的Miner法则以及文献[15]中模型的结果对比可知，改进的非线性预测模型预测精度均有一定的提升，预测结果与实际试验数据更为接近；在文中改进的2种方式中，直接采用实时疲劳损伤对交互因子进行修正的分析结果更为准确一些，实时损伤程度越大，交互因子的作用效果则更为明显。

表1 Q235B焊接接头在3级载荷作用下采用不同模型得到的疲劳寿命预测结果

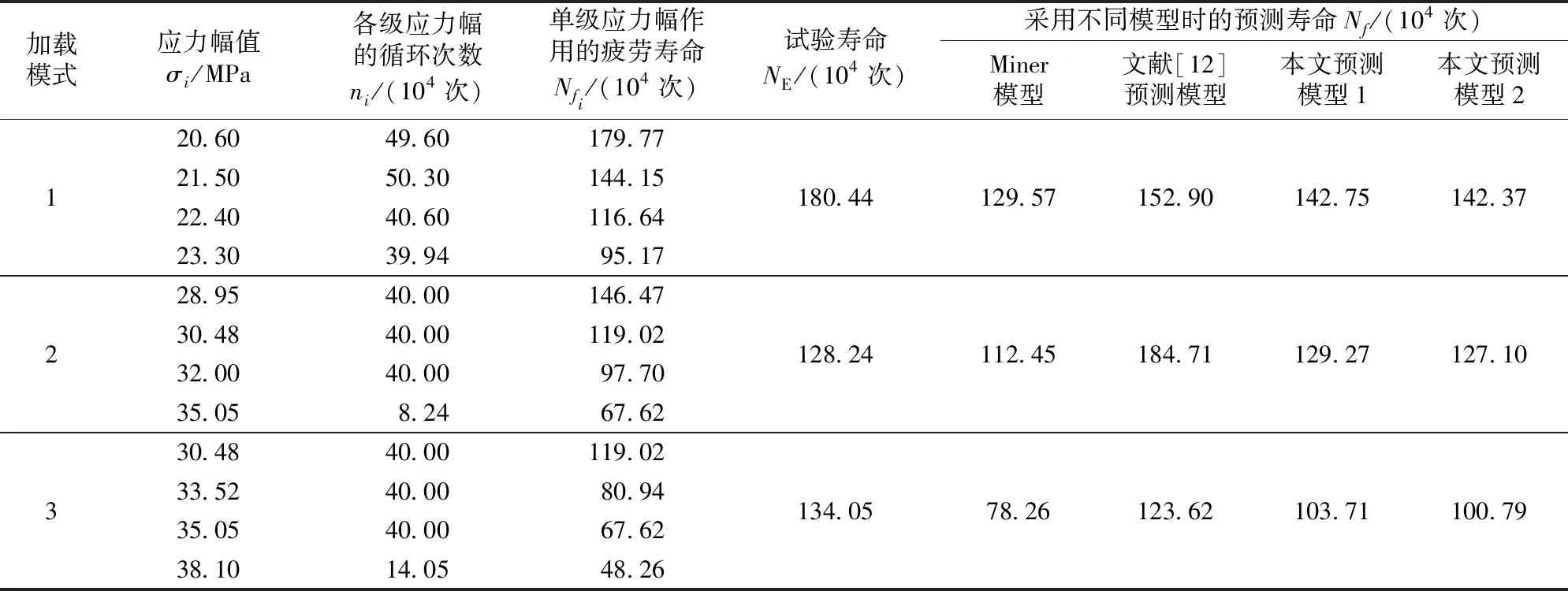
表2 Q235B焊接接头在4级载荷作用下采用不同模型得到的疲劳寿命预测结果

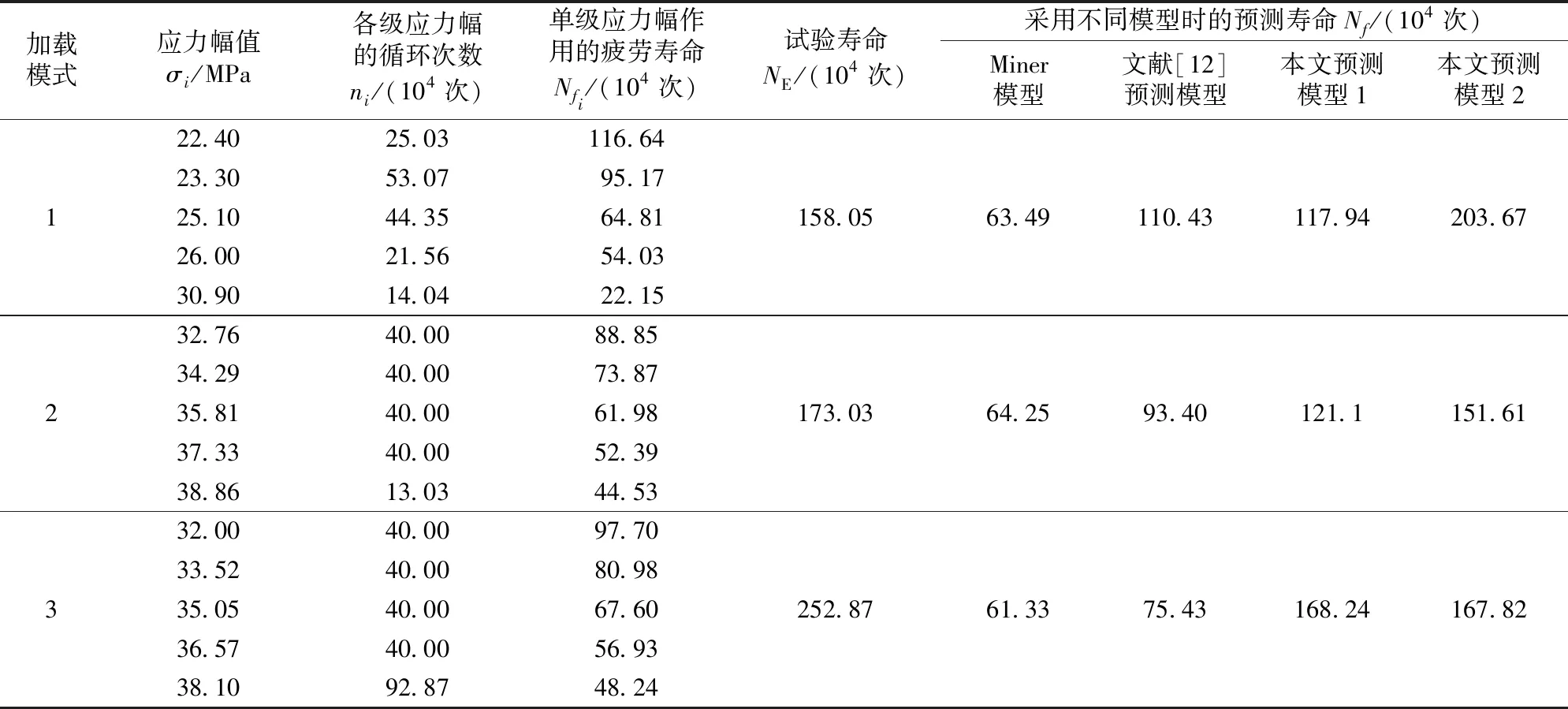
表3 Q235B焊接接头在5级载荷作用下采用不同模型得到的疲劳寿命预测结果

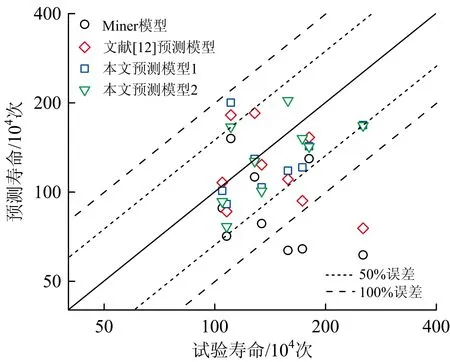
图1 多级载荷作用下Q235B焊接接头疲劳寿命结果对比

图2 4级载荷作用下铝合金6082T6接头疲劳损伤结果对比

表4 铝合金6082T6在4级载荷作用下采用不同模型得到的疲劳寿命预测结果

注：表中第3列各级应力幅的循环数所对应第4级应力幅的循环数n4为试验值。

4 结 论

(1)利用变幅载荷的应力比、循环比以及实时损伤状态参量对相邻载荷间交互因子进行修正，所改进的非线性疲劳寿命预测模型能较好地处理变幅载荷加载的历史效应，在不需要引入额外参数的前提下，可有效地处理变幅载荷加载历史对损伤累积的影响，能够较为准确地对焊接结构进行疲劳寿命预测。

(2)根据Q235B焊接接头的疲劳寿命对比结果，在不同级数的变幅载荷作用下，改进模型均具有可行性，在精度方面也有不同程度的提高，预测分析结果更接近于试验结果。

(3)根据铝合金焊接接头的疲劳寿命对比结果，在递增、递减以及随机的变幅载荷作用下，改进的非线性疲劳寿命预测模型均能对焊接接头疲劳寿命进行有效的预测。与文献模型以及传统的Miner模型相比，预测精度有明显的提升，与文献中所给出的试验结果更加接近。

(4)改进的非线性疲劳寿命预测模型涉及的参数仅为2个，且比较容易通过试验确定，计算递推格式也较为简单，不需要多层嵌套，非常便于应用于实际焊接结构的疲劳寿命预测。