基于IPSO-Capsule-NN模型的中欧班列出口需求量预测

冯芬玲，阎美好，刘承光，李 万

(中南大学 交通运输工程学院，湖南 长沙 410075)

中欧班列开通至今，凭借着速度快、频率高、安全性高和受自然环境影响小等优势开行数量和货物分担率不断提高，截至2018年10月开行数量已突破11 000列，运行线路65条，成为国际物流中陆路运输的骨干模式。中欧班列的常态化运行有力促进了中欧以及沿线各国之间的经济贸易往来，为准确判断中欧班列运输市场的发展趋势及增长空间，对中欧班列出口需求量进行预测显得尤为重要。中欧班列出口需求量预测的准确性不仅利于国家资源配置，也是铁路运输部门调整经营管理方式的依据。与此同时，精准的预测也对中欧班列开行方案研究、营运策略制定、基础设施建设、价格制定和提高市场分担率具有重要现实意义。

作为较为成熟而且应用范围最广的神经网络模型，BPNN仍然存在如何确定神经网络的隐含层数、隐含层神经元数、学习率以及迭代次数的问题，并且存在收敛速度慢、容易陷入局部最优等缺点，预测会产生很强的波动性，因此短期货运量预测的精确度不高。Geoffrey Hinton等[18]于2017年10月提出了胶囊网络(Capsule Network)，与其他模型相比，胶囊网络通过动态路由算法增强了模型的拟合能力和泛化能力，在图像识别方面降低了45%的错误率。因此，为了对中欧班列出口需求量进行精准的预测，本文提出一种非线性递减惯性权重并引入Levy飞行对PSO进行改进，并将改进的PSO与具有较好拟合能力和泛化能力的胶囊神经网络(Capsule-NN)相结合，对中欧班列出口需求量进行预测。

1 中欧班列出口需求量影响因素

中欧班列出口需求量受自然资源、外部经济需求、铁路运输系统供给、政府政策和其他运输方式竞争等5个方面因素的共同影响。

(1)自然资源。国际货物运输需求产生的主要原因之一就是自然资源分布不均衡。由于资源集中在某一国家或地区而其他国家或地区资源匮乏，或某些资源富集国家或地区消费需求较小，抑或是受技术条件限制使用率低，便会发生资源从富集国家或地区流向其他国家或地区的现象，从而引发国际货物运输需求；另一方面，由于全球产业布局调整，我国内陆生产的高新技术产品要以更快的速度运往欧洲，而中欧班列的开通打破了内陆城市的运输限制，同时带动了中欧之间的贸易往来。

(2)外部经济需求。经济的发展可以带动运输需求数量的上升，反之则会下降。一般经济状况良好的国家和地区对外界往往具有较强的辐射能力和吸引能力，从而会有较大规模的货物生成量，此外不同经济发展时期运输结构需求也不同。中欧班列出口需求量不仅受国民经济总量影响，还受经济结构的影响。其中，经济总量因素包括国民经济发展规模和工业发展规模等，各种经济结构因素包括产业结构和工业结构等。

(3)铁路运输系统供给。运输供给应是运输生产者愿意同时能够提供的生产运输服务能力。中欧班列运输过程中途经多个国家，通达国家的铁路发展水平及中欧班列主要载体--中欧班列运输通道从侧面反映了中欧班列的运输能力和通过能力，而基础设施建设程度和运输能力会影响贸易进出口运输方式的选择。目前，中欧班列运输通道可分为4部分，依次是东南亚铁路网络、中国境内运输通道、亚欧间铁路运输通道及欧洲货运网络。

(4)政府政策。积极采取对外开放政策的国家会注重加强与他国间的经济、文化、技术等方面的交流与合作，加大本国的进出口贸易活跃度。中欧班列出口需求量在这方面受到的影响可以归纳为2个方面，一方面是中国与欧、亚国家合作意向不断增加，中欧班列通达国家数量也在不断上升，为班列的常态化运行创造了良好氛围；而另一方面，由于在班列运行初期政府补贴支持力度大，使得沿海地区部分海运需求转移到中欧班列引起运量增加，但当补贴逐渐退出时，运价回归市场调节，运费优势将不会存在。

(5)其他运输方式竞争影响。在市场份额一定的情况下，铁路、公路、水运、航空等交通运输方式之间呈现出此消彼长的竞争关系，每种运输方式的革新和进步在提升自身竞争力的同时也影响着其他运输方式的市场分担率。

综合中欧班列出口需求量影响因素分析，选取以下几类指标进行预测分析。

①我国同中欧班列通达各国的贸易进出口额，用以衡量中欧班列出口运输需求大小；中国向欧洲出口的包括机械设备、电子设备、粮食、蔬菜及肉类等十几类货物的国内产量、通达各国粮食产量，用以衡量中欧贸易分货物品类运输需求大小。②中欧班列通达各国的国内生产总值(GDP)、工业增加值、农业增加值，我国3大产业及交通运输产业的生产总值，用以衡量国民经济发展水平。③通达各国铁路总里程数、人均线路里程，用以反映各国铁路的发展程度和运输能力。④对外直接投资(OFDI)是企业参与国际竞争和合作、融入世界经济的重要方式，与此同时它也促进了贸易出口，因此选取中国对“一带一路”沿线64个国家的对外直接投资总和作为政府政策指标，用以衡量国家对外开放的程度，尤其是“一带一路”国家战略提出后，中国企业“走出去”的实际情况。⑤我国各种运输方式(水运、公路、铁路、航空)的出口贸易额，可以衡量各种运输方式在国际货物运输市场中的竞争力。

2 胶囊神经网络(Capsule-NN)

由于中欧班列出口需求量一方面整体波动较大，另一方面受多种因素的共同影响，且与各个影响因素存在着复杂并难以量化的非线性关系，在拟合预测时，浅层网络在函数表达能力上往往表现不足，相比之下深层网络则可能仅需要较少的计算单元就能获得较好的效果。然而网络在实际应用中也不是越深越好，除了造成计算资源和时间的浪费，更主要是会出现梯度消失的问题。目前，解决梯度消失的方式大致可以分为几种类型：对激活函数进行改进；层归一化；对权值初始化方式进行优化；直接调整构建新颖的网络结构，如胶囊网络(Capsule Network)。与全连接神经网络不同，胶囊网络采用的动态路由算法并不会丢弃任何信息，有效降低了识别错误率，从而增强了模型的非线性拟合能力和泛化能力。因此，本文选用胶囊网络并对其进行一定改进用以预测中欧班列出口需求量，以期得到较好的预测效果。

胶囊网络与全连接神经网络的连接方式相同，区别在于胶囊网络采用了胶囊层，而胶囊层利用了动态路由算法。具体来说，区别1在于：全连接网络在输入时是线性加权求和，而胶囊网络在线性求和这一阶段还增加了1个耦合系数cij。cij按如下公式计算加权和，可得到胶囊网络的输入sj为

(1)

(2)

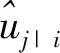
耦合系数cij通过迭代的动态路由过程计算得到，计算公式如下。

(3)

(4)

式中：bij是第i个低级胶囊单元与第j个高级胶囊单元之间的偏置，初始值为0，这样得到的耦合系数cij会趋于一般化，还不能表现出前后2层胶囊之间的关系，因此需要通过bij的更新来更新cij；m为初始化相似度权重bij的个数；vj是高级胶囊层中第j个胶囊单元(即下一层胶囊网络的输出)。动态路由算法的迭代次数一般设定3为佳。

区别2在于：全连接神经网络选用的激活函数通常都是Sigmoid, tanh等函数，但在胶囊网络中构造了新的激活函数Squashing为

(5)

式中：函数第1部分是输入向量sj的缩放尺度，第2部分是输入向量sj的单位向量，Squashing函数保留了输入向量方向的同时又将输入向量的模压缩到[0, 1)之间。

本文结合胶囊网络的思想，构建了Capsule-NN预测模型用以对中欧班列出口需求量进行预测，提出的胶囊神经网络(Capsule-NN)结构如图1所示。

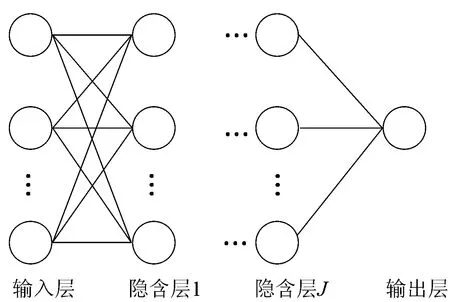
图1 Capsule-NN结构

其中，输出层采用上述提到的胶囊层；隐含层采用非线性回归层，设第J个隐含层的输入为xJ，即上一层的输出，第J个隐含层的输出为oJ，第J层与第L层之间的权值和阈值分别为wJL和bJ，则

oJ=sigmoid(wJLxJ+bJ)

(6)

由于Sigmoid函数可以把实数域光滑地映射到(0，1)空间，函数值恰好可以解释为属于正类的概率(概率的取值范围是0～1)，输出范围有限使得优化较为稳定；另外，Sigmoid函数单调递增，连续可导且导数形式非常简单，因此对于求导、连续求导或是处理二分类问题时，一般选用Sigmoid函数。预测问题本质上也是1种二分类问题，所以本文提出的模型中第1层到第h-1层的激活函数选用Sigmoid函数，最后一层采用胶囊层。充分发挥Sigmoid函数的非线性拟合能力，与此同时利用胶囊层防止神经网络过拟合并提高模型的泛化能力，从而增加预测的精度。

除耦合系数cij需通过动态路由完成更新，整个网络的其他参数以及Capusle内的Wij则需要采用Adam算法，根据损失函数Lc进行训练完成更新。

(7)

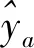
Capsule-NN的训练步骤如下。

Step1：把数据归一化到[0，1]之间，得到归一化后的数据。

Step2：初始化训练次数NCa和学习速率cCa，以及每个隐含层的权值wJL和阈值bJ。

Step3：把数据输入模型的第1层，即输入层，然后经过非线性函数Sigmoid计算得到输入层的输出结果。

Step4：把Step3得到的结果作为第1层隐含层的输入，然后经过非线性函数Sigmoid计算得到输出结果。

Step5：重复执行Step4直到执行到最后1层隐含层。

Step6：将最后1层隐含层的输入经过动态路由算法计算后得到输出结果，并作为输出层的输出。

Step7：利用输入数据的标签和Aeam算法对模型的权值和阈值进行调整。

Step8：重复执行Step3—Step7，直到达到最大迭代次数NCa或神经网络收敛。

3 改进粒子群优化算法(IPSO)

3.1 PSO原理

PSO是一种基于种群的全局随机搜索算法。在PSO算法中，每个优化问题的潜在解都可以视为搜索空间中的1个粒子，粒子凭借自身的经验和最优粒子的经验在不断搜寻最佳位置的飞行中调整位置。假如在1个多维搜索空间中，有Q个粒子共同组成1个群体，每次迭代的过程中各个粒子会根据个体极值pq和全局最优解gt更新自身速度和位置。各个粒子在搜索这2个最优解时将按照如下公式来更新速度和位置。

vq,t+1=w×vq,t+c1×b′×(pq-xq,t)+c2×b′×(gt-xq,t)

(8)

xq,t+1=xq,t+λ×vq,t+1

(9)

式中：xq,t和vq,t分别表示第q个粒子在第t次迭代过程中的位置和速度；w表示惯性权重；c1和c2表示学习因子；b′是[0,1]之间的随机数；λ是速度系数，在本文中λ=1。

3.2 对PSO算法的改进

由于在基本的PSO算法中各个粒子同时向自身和种群的历史最佳位置聚集，出现快速趋同效应，容易产生陷入局部最优或早熟收敛等问题[19]。为克服PSO算法的这种不足，本文提出利用非线性递减惯性权重和Levy飞行来改善PSO的全局寻优能力和收敛速度，以此提高PSO算法的性能。

1)非线性递减惯性权重

在基本的PSO算法中，惯性权重w值固定一方面会削弱算法的全局寻优能力，另一方面也会降低算法的收敛速度。为此，本文将wt改为如下的形式。

(10)

式中：t为当前迭代次数；wmax和wmin分别代表w的最大值和最小值；tmax为最大迭代次数。

改进后的惯性权重w值的变化趋势如图2所示。当t较小时，wt接近wmax且w的减少速度较慢，从而保证了算法的全局寻优能力；t逐渐增大，wt开始以非线性速度快速递减，当t接近tmax时，wt接近wmin，wt的减小速度变慢，进而保证了算法的局部寻优能力，通过让惯性权重动态非线性递减使算法能灵活调整局部和全局的寻优能力。

图2 惯性权重w的变化趋势

2)Levy飞行

在PSO算法迭代的后期，粒子群的搜索范围会不断缩小。为了增大粒子的搜索范围，引入Levy飞行。在自然界中，“Levy飞行”搜索策略是大多数动物在不确定的环境中找到食物的最理想方式[20]。这种搜索方式的优势在于动物一方面通过短距离蹦跳保证对自身周围小范围内的仔细搜寻，另一方面通过偶尔较长距离的行走保证能进入另一个搜索区域，从而扩大不断搜索的最小空间。Levy飞行是一种非高斯随机化过程，一般采用 Mantegna 提出的模拟Levy飞行路径的公式来计算Levy飞行搜索路径S。

(11)

(12)

(13)

式中：S为Levy飞行路径；参数β的取值范围为0<β<2，一般取β=1.5；μ和υ为正态分布随机数；σμ和συ为正态分布的标准差；Γ为标准Gamma函数。

4 IPSO优化Capsule-NN算法流程

IPSO优化Capsule-NN算法的步骤如下。

Step1：初始化参数。明确算法中的种群规模大小Q、学习因子c1和c2、迭代次数NIPSO以及各个粒子的位置xq,t和速度vq,t的限定取值区间。

Step2：初始化粒子的位置xq,0和速度vq,0。随机生成1个粒子xq,0(h1,h2,…，hR,ε,Nd)，h1,h2,…，hR分别为第1层、第2层至第R层隐含层的神经元个数，ε为Adam算法的学习率，Nd为Adam算法的迭代次数。

Step3：确定粒子的评价函数。将Step2中随机生成的粒子xq,0对Capsule-NN的参数进行赋值。将数据分为训练、验证和预测样本，并将训练样本输入进行神经网络训练，当达到迭代次数限制后便会得到训练样本的输出值yz以及验证样本的输出值yz′。而种群粒子xq的适应度值fq定义为

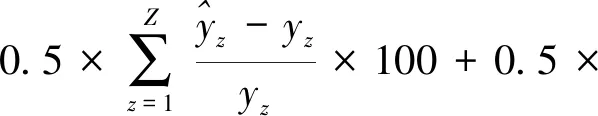
(14)

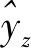
由于本文预测的中欧班列出口需求量属于时间序列，近年的变化对未来的影响更大。因此，利用训练样本的拟合误差和验证样本的验证误差作为适应度函数，一方面在保证模型对数据良好拟合度的同时有效避免过拟合；此外，由于验证样本的误差能直接反映出模型的预测效果，还可以得到对未来预测较好的Capsule-NN模型。设2个样本误差的权重均为0.5。

Step4：按照第2节的训练步骤训练Capsule-NN模型。计算各个粒子的适应度值fq，根据初始粒子的适应度值确定个体极值pq及群体极值gt。

Step5：按照式(8)和(9)结合个体极值及群体极值更新粒子自身的位置xq,t和速度vq,t；然后计算新粒子的适应度值，根据新粒子的适应度值分别更新粒子的个体和群体极值。

Step6：让粒子按一定概率PLevy进行Levy飞行。

Step7：满足算法的最大迭代次数NIPSO或适应度函数收敛，则算法结束，将影响因素的预测值输入到用最优粒子训练好的Capsule-NN模型中，输出中欧班列出口需求量预测值，否则返回Step5。

5 实证分析

自中欧班列开行以来，定义范围不断调整，根据《中欧班列建设发展规划(2016—2020年)》，中欧班列的范围已扩大到中国与欧洲以及“一带一路”的沿线各国，包括中亚班列在内的所有国际集装箱班列都统称为中欧班列。而在2011年中欧班列开行之前，中欧、中亚之间一直都有铁路运输方式的进出口贸易，2011年之后由于定义范围的调整，中欧班列集装箱的统计口径并未完全统一，数据不准确；另一方面开行至今只有7年数据，而且受政策影响近年班列数呈井喷式增长，以集装箱量预测结果并不准确且意义不大。此外，随着中欧班列品牌影响力不断增强，搭载的货物品类也日益丰富，因此将中国与这些国家间自2001年至2017年历年贸易通过的铁路国境站的出口货运量作为中欧班列出口需求量并对其进行预测，从而判断中欧班列运输市场的发展趋势及未来的增长空间。

中欧班列出口需求量变化趋势整体波动较大，主要是因为2001—2008年随着经济水平的提升，出口需求量逐年递增，2008年以后受全球金融危机的影响，欧洲国家经济受到很大冲击，其中部分国家爆发主权债务危机，中欧贸易受到较大影响，因此2009年和2010年出口需求量大幅下降。2010年以后随着经济的好转出口需求量再次上升，直到2012年后，世界经济进一步呈现出分化和割裂的趋势。作为世界经济中最为薄弱的一环欧洲经济再次面临冲击，导致出口需求量在2013—2015年也再次受到影响。近年来随着欧洲国家结构改革取得一定成效，经济开始复苏，另外中国政府提出的“一带一路”倡议也加强了中国与欧洲和亚洲之间的贸易往来，出口需求量开始逐年上升。

5.1 中欧班列出口需求量预测影响指标选取

根据第1节分析选择的影响因素指标，收集2001—2017年间的数据。全部数据来源于中国铁道年鉴、国家铁路局网站、中国口岸年鉴、中国贸易外经统计年鉴、中国对外直接投资统计公报及联合国数据库等。

将影响因素输入Capsule-NN模型前，首先需要对全部影响因素进行相关性分析，并根据相关性大小选取最终的影响指标来对出口需求量进行预测。由于Spearman秩相关性分析法能在数据在逻辑范围不等距且不符合任何分布的情况下有效度量2个序列数据之间的相关性程度，故采用此方法对影响因素进行相关性分析。对第1节选取的相关影响因素进行相关性分析，结果如表1所示。其中，有4类指标共11个因素与中欧班列出口需求量的Spearman相关度较高，均大于0.9，因此将这11个因素作为Capsule-NN的输入。

由于影响因素对出口需求量预测的影响较大，利用相关性较高的指标理论上可以得到更好的预测结果，而历史指标与未来出口需求量的相关性较低。因此，本文利用ARIMA对未来指标进行预测，进而对出口需求量进行预测。

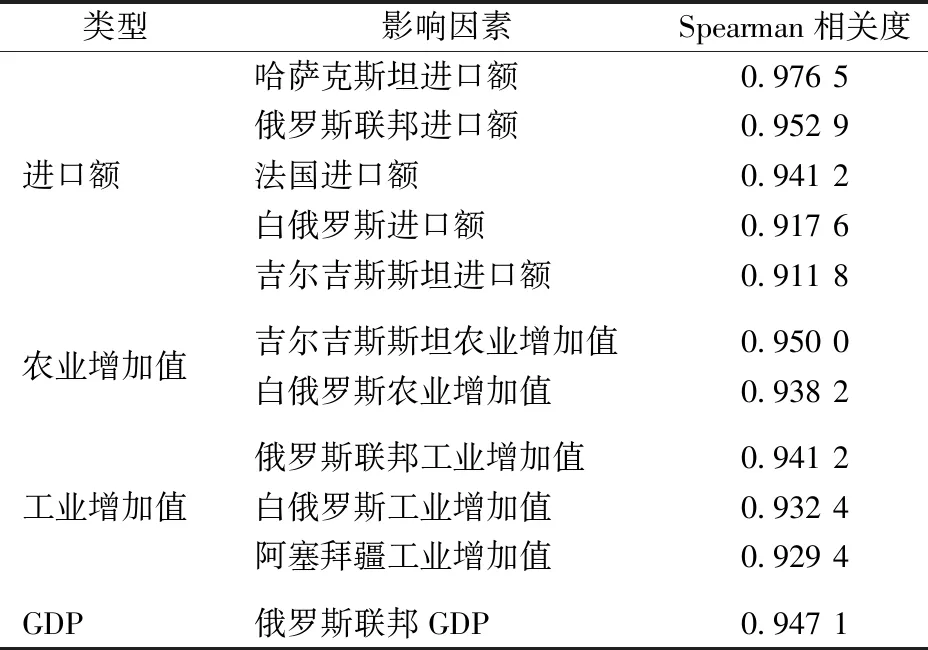
表1 影响因素及相关性

5.2 仿真条件

算法的试验环境为python3.6，采用python语言编写PSO计算程序，并利用TensorFlow深度学习库建立了8种预测模型，依次是：包含1层隐含层的Capsule-NN模型(Capsule-NN3)、PSO优化包含1层隐含层的Capsule-NN模型(PSO-Capsule-NN3)、IPSO优化包含1层隐含层的Capsule-NN模型(IPSO-Capsule-NN3)、包含2层隐含层的Capsule-NN模型(Capsule-NN4)、PSO优化包含2层隐含层的Capsule-NN模型(PSO-Capsule-NN4)、IPSO优化包含2层隐含层的Capsule-NN模型(IPSO-Capsule-NN4)、包含1层隐含层的BP神经网络模型(BPNN3)以及包含2层隐含层的BP神经网络模型(BPNN4)。针对相同的影响因素数据，进行中欧班列出口需求量预测对比实验。

首先，需要对实验中的时间序列数据进行归一化处理，将数据归一化到[ymin，ymax]之间。

(15)

式中：y′为归一化后的值；ymin和ymax分别为归一化后的最小值和最大值；x′为原始值；xmin和xmax分别为原始数据的最小值和最大值。为使Capsule-NN的拟合效果和预测效果更好，在本文中设定ymin=0.1，ymax=0.9。

采用平均绝对误差(rMAE)和平均绝对百分误差(rMAPE)对实验的误差进行评价。

(16)

(17)

模型的训练样本为2001年到2013年共13年的数据，验证样本为2014到2015年共2年的数据，预测样本为2016到2017年共2年的数据。由于Capsule-NN的输入为11个影响因素，输出为中欧班列出口需求量，因此Capsule-NN的输入层神经元个数为11个，输出层神经元个数为1个。Capsule-NN的内部参数训练采用Adam算法。BPNN3采用M-2M+1-1结构，其中M为输入层的神经元个数即11，学习率为0.01，训练次数为1 000次；BPNN4采用M-2M+1-2M+1-1结构，M同理取11，学习率为0.01，训练次数为1 000次。PSO算法参数设置：种群数量为5，进化次数为20次，学习因子为c1=c2=1，粒子xq(h1,h2,ε,Nd)中h1，h2，ε和Nd的取值范围分别为[10,100]，[10,100]，[0.001,0.2]和[100,1000]，速度取值范围分别为[-10,10]，[-10,10]，[-0.02,0.02]和[-100,100]。IPSO中，wmax=0.9，wmin=0.1,PLevy=0.1。PSO中，w=0.1。

5.3 中欧班列出口需求量预测实验

如表2所示为8种模型的预测误差。容易看出，IPSO-Capsule-NN4具有最小的预测误差，其中rMAE为7.18万t，rMAPE为0.79%。该模型适合于中欧班列出口需求量预测。

表2 中欧班列出口需求量的预测误差

IPSO-Capsule-NN4，PSO-Capsule-NN4，Cap-sule-NN4和BPNN4的预测误差分别比IPSO-Capsule-NN3，PSO-Capsule-NN3，Capsule-NN3和BPNN3的小，说明包含2层隐含层的神经网络比包含1层的预测效果好。

此外，Capsule-NN4和Capsule-NN3相对于BPNN4和BPNN3具有更好的预测结果，说明Capsule-NN具有更好的拟合能力和泛化能力。

IPSO-Capsule-NN3和IPSO-Capsule-NN4比PSO-Capsule-NN3和PSO-Capsule-NN4具有更小的预测误差，证明本文提出的IPSO相对于PSO具有更好的全局寻优能力，可以获得更好的神经网络结构参数以改进Capsule-NN的预测效果。

图3是利用PSO优化Capsule-NN的适应度变化对比。其中，图3(a)表示IPSO-Capsule-NN3和PSO-Capsule-NN3的适应度对比，图3(b)表示IPSO-Capsule-NN4和PSO-Capsule-NN4的适应度对比。由图3可知，利用IPSO优化Capsule-NN不仅得到了更小的适应度值，收敛到最小适应度值的速度也更快。这表明改进后的PSO算法具有更好的全局寻优能力和更快的收敛速度。

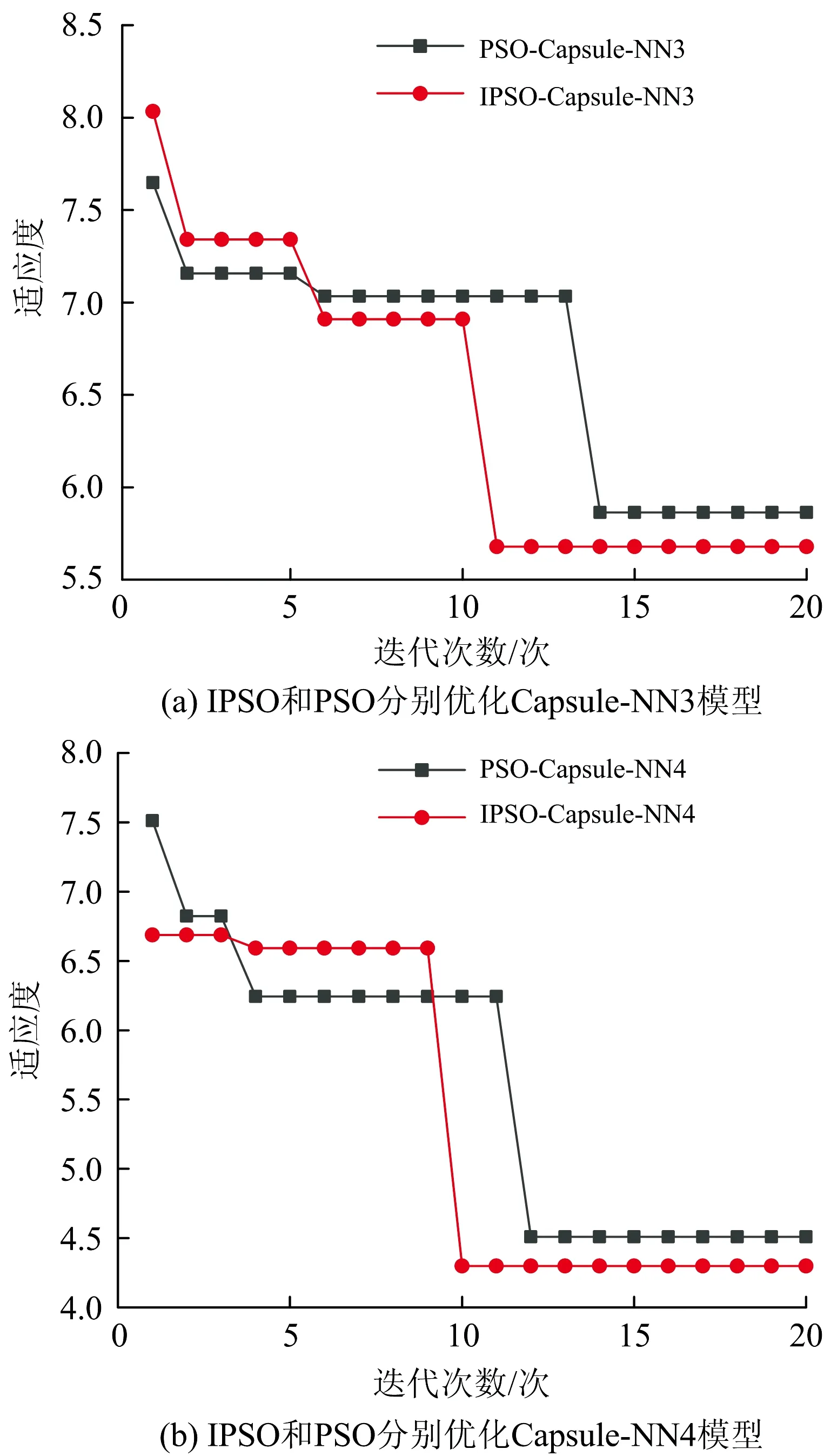
图3 适应度变化对比

IPSO-Capsule-NN4的隐含层节点数、迭代次数以及学习率随PSO算法迭代次数变化而变化的状态如图4所示。由图4(a)看出，第1层隐含层h1和第2层隐含层h2的神经元数量最终分别稳定在10个和93个；图4(b)显示了IPSO-Capsule-NN4的迭代次数Nd随PSO的迭代次数变化，最终稳定在729次；图4(c)表示学习率ε随迭代次数变化，最终稳定在0.067。

图4 IPSO-Capsule-NN4最优粒子参数变化

5.4 中欧班列出口需求量预测

根据5.3小节的预测实验已经证明IPSO-Capsule-NN4能较好地预测中欧班列出口需求量，因此本节将利用该模型对中欧班列出口需求量进行预测，预测时间段从2018年到2019年。由于并不知道这2年影响因素的值，所以需要先对这些影响因素的值进行预测。本文采用ARIMA来拟合各个影响因素并进行预测，根据赤池信息量(AIC)准则和贝叶斯信息量(BIC)准则，在所有通过检验的模型中使得AIC或BIC函数达到最小的模型为相对最优模型。因此，利用最小的AIC及BIC值进行模型选取并进行预测。ARIMA的模型参数(p,d,q)(其中，p为自回归模型阶数，d为差分次数，q为移动平均模型阶数)及影响因素预测结果如表3所示。

表3 影响因素预测值

将表3的数据输入到IPSO-Capsule-NN4模型中便可得到中欧班列2018年到2019年的出口运量预测值，如表4所示。中欧班列历年出口需求量拟合值及预测值与实际值对比如图5所示，2001—2017年的数据为模型通过神经网络训练的拟合值，2018—2019为模型训练学习后得到的预测值。由表4可知，中欧班列出口需求量呈现上升的趋势，2019年达到1 007.29万t。政府应继续加强我国铁路口岸站基础设施的建设，政策的制定也要根据中欧班列出口需求量进行相应的调整。

表4 中欧班列出口需求量预测值

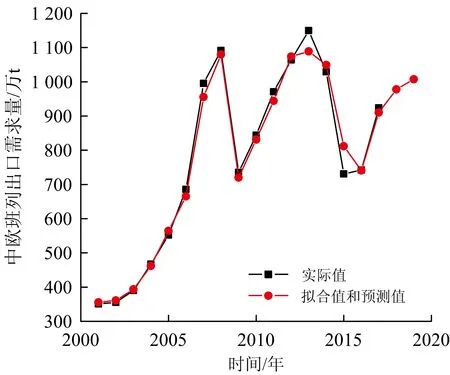
图5 中欧班列出口需求量预测值与实际值对比

6 结 论

(1)将拟合能力和泛化能力更强的Capsule-NN运用到中欧班列出口需求量的预测，提高了预测精度，有助于铁路运输部门更好地进行规划和管理。中欧班列出口需求量预测呈现上升趋势，政府和铁路运输部门应继续加强铁路口岸基础设施建设，并针对预测值进行政策调整。

(2)利用Spearman秩相关性分析，得到11个因素与中欧班列出口需求量的相关性较高，适合作为中欧班列出口需求量的影响因素。

(3)利用非线性递减变化的权重和Levy飞行改进PSO，增强了PSO的全局寻优能力并提高了PSO的收敛速度。

(4)将IPSO和Capsule-NN相结合，利用IPSO优化Capsule-NN的隐含层神经元数量、迭代次数和学习率，克服了人为确定模型参数的不足，使其对中欧班列出口需求量具有更好的预测效果。与PSO相比，IPSO可以获得更优的参数来优化Capsule-NN。

(5)与其他几个模型相比，Capsule-NN具有2层隐含层时，IPSO-Capsule-NN模型具有最小的预测误差，rMAPE为0.79%，预测精度高，模式适合于中欧班列出口需求量预测。2019年出口需求量预测值达到1 007.29万t。