调磁块连接方式对磁场调制型磁性齿轮传动性能的影响

王均刚，徐帅睿，欧阳爱国，墨蕊娜，肖毅华

(1.华东交通大学 机电与车辆工程学院，江西 南昌 330013；2.华东交通大学 理学院，江西 南昌 330013)

机械齿轮通常用于传递机械各部件间的动力和运动[1]。然而，因机械齿轮系统传动依赖于齿廓间的接触应力，存在某些问题[2-3]，例如物理接触造成的摩擦损失、噪音、振动，并且需要进行间断的维护。相较于传统机械齿轮，磁性齿轮传动因机械摩擦产生的损失较小，具有更小的噪声和振动，并且不需要额外的维护[4-5]。而且，因为它是非接触式驱动的，如果施加过载扭矩，磁性齿轮能够通过无接触滑动防止过载，当过载扭矩消失后轮齿重新啮合并能正常运作[6]。

早期的磁性齿轮转矩密度过低，无法运用于实际工程中。随着对磁性齿轮研究的深入，有学者发现：采用同轴拓扑结构能大幅的提高磁性齿轮转矩密度，大大提高永磁磁极的利用率[7]。但人们很快发现，在保留同轴拓扑的前提下，想要实现齿轮的变速传动必须使得输入和输出侧具有不同的磁极对数，然而仅仅通过改变磁极对数会使输入和输出侧的磁极无法有效耦合，内、外转子间无法产生有效力矩[8]。直到21世纪初，国外学者Atallah等[9]通过低速谐波电机运行原理受到启发，提出了磁场调制型磁性齿轮磁场有效耦合的条件，通过在内转子磁极与外转子磁极间均匀布置调磁块，通过调磁块对气隙磁场进行调制，使内、外转子磁极产生的磁场实现有效的耦合；且内转子磁极对数Nin、外转子磁极对数Nout和调磁块数N需满足Nin+Nout=N。调磁环由沿圆周均匀布置的调磁块通过一定的连接方式组成，调磁块的形状和连接方式将影响调磁环对气隙磁场的调制效果，国内外学者对磁性齿轮调磁环的设计和优化做了大量的研究。Abdelhamid等[10]利用有限元分析方法从峰值转矩和涡流损耗2个方面对提出的4种调磁环设计进行了分析，对4种设计对磁性齿轮传动性能的影响做出了评估。Kim等[11]针对不同形状的调磁块，采用基于二维数值模拟的非线性有限元方法，比较了同轴磁性齿轮的传递力矩特性分析。Xiao等[12]提出了一种具有高扭矩和高永磁体利用率的新型双磁通调磁环同轴磁性齿轮，通过试验证明了该调磁环大幅增强了有用的谐波磁场，提高了磁性齿轮的扭矩。目前，为提高磁性齿轮的传动性能对调磁块的形状和结构参数进行优化的研究已有很多，而研究其连接方式对磁性齿轮传动性能的研究较少，因此有必要对调磁块的不同连接方式进行研究。

本文分析调磁块连接方式对磁性齿轮传动性能的影响，提出3种调磁块的连接方式，利用有限元分析软件分别对3种连接方式下的结构进行仿真分析，研究3种连接方式对磁性齿轮传动性能的影响，为磁场调制型磁性齿轮调磁环的设计加工提供一定的参考和依据。

1 无调磁块时气隙磁感应强度分布

径向磁场调制型磁性齿轮拓扑结构如图1所示。由图1可见：径向磁场调制型磁性齿轮由内、外转子铁轭，内、外转子气隙， 内、外转子永磁体以及调磁块组成；内、外转子永磁体分别通过表面安装固定于内、外转子铁轭，为了防止涡流现象造成的能量损失，内外转子铁轭和调磁块均采用硅钢片轴向叠合而成，且相邻片间存在绝缘镀层。

图1所示调磁块的排布为理想排布方式，实际加工中，一般需要在调磁块间添加连接桥，以便确定调磁块之间相对位置。对无调磁块时进行讨论，为了使计算气隙磁感应强度分布更加简便，做出如下假设：内、外转子永磁体产生的磁场为正弦波形；内、外转子铁轭磁导率为无穷大。

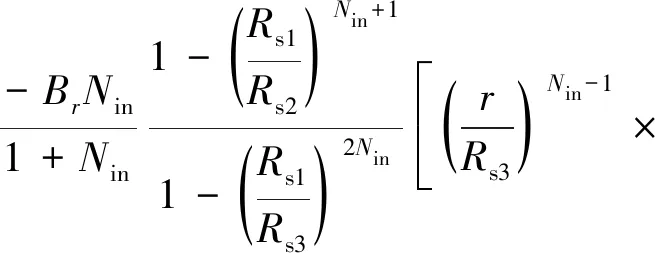
设标量磁动势为变量，在求解域中建立拉普拉斯、准泊松方程[13]，可以求出内转子永磁体单独作用下气隙中径向和切向磁感应强度Br1(r)和Bθ1(r)分别为

cos[Nin(θ-ωit)+Ninθ10]=

A(r)cos[Nin(θ-ωit)+Ninθ10]

(1)

sin[Nin(θ-ωit)+Ninθ10]=

B(r)sin[Nin(θ-ωit)+Ninθ10]

(2)

外转子永磁体单独作用下气隙中径向和切向磁感应强度Br2(r)和B(2(r)分别为

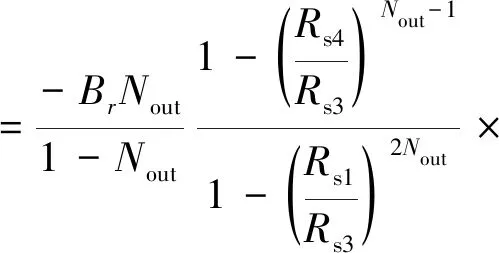
cos[Nout(θ-ωot)+Noutθ20]=C(r)cos[Nout(θ-ωot)+Noutθ20]

(3)

(4)

式中：r和θ分别为测量点在极坐标下的极矩和相角；Br为测量点的磁感应强度的大小；Rs1和Rs2分别为内转子内、外半径；Rs3和Rs4分别为外转子内、外半径；ωi和ωo分别为内、外转子的转速；t为时间；θ10，θ20分别为内、外转子初始位置角；A，B，C和D均为待定系数，且只与r有关、而与θ无关。

2 引入调磁块后气隙磁感应强度分布

引入调磁块后，调磁块将原来的气隙空间分为内、外转子气隙空间。由于调磁块磁导率远大于相邻的空气槽，内、外转子磁极产生的磁力线将向调磁块聚集，从而使调磁块相邻空气槽的磁力线密度变小。此时的磁感应强度[14]为

BM=B0(λaer-λbeθ)

(5)

式中：B0和BM分别为引入调磁块前后的磁感应强度；λa和λb分别为复磁导函数的径向分量和切向分量；er和eθ分别为径向和切向方向的单位向量。

把λa和λb用傅里叶级数表示，代入式(5)中，即可求出内外转子气隙磁感应强度表达式。根据叠加原理，内转子气隙的磁感应强度的径向和切向分量Br-in和Bθ-in分别为

Br-in=λ0-inE(rin)cos[Nin(θ-ωit)+Ninθ10]+λ0-inF(rin)cos[Nout(θ-ωot)+Noutθ20]+

jNinθ10]+ejkcos[Nojk(θ-ωojkt)+

jNoutθ20]}

(6)

Bθ-in=λ0-inE(rin)sin[Nin(θ-ωit)+Ninθ10]+λ0-inF(rin)sin[Nout(θ-ωot)+Noutθ20]+

jNinθ10]+fjksin[Nojk(θ-ωojkt)+

jNoutθ20]}

(7)

式中：λ0-in为傅里叶级数；rin为内转子气隙测量点在极坐标下的极矩；E和F均为待定系数，且与极矩rin有关；ajk，bjk，ejk，fjk均为常数；Nijk，Nojk均为磁场谐波分量的空间极对数；ωijk，ωojk均为磁场谐波分量对应的旋转速度。

同理，也可推导出外转子气隙的磁感应强度的径向和切向分量Br-out和Bθ-out。

由麦克斯韦张量法[15]可得径向磁场调制型磁性齿轮内、外转子的最大转矩Tin和Tout分别为

(8)

(9)

式中：Lc为磁性齿轮的轴向长度；μ0为真空磁导率；Rin和Rout分别为内、外转子气隙的半径。

3 不同连接方式对磁性齿轮性能的影响

3.1 不同连接方式下磁性齿轮磁力线分布

理想条件下磁性齿轮磁力线分布如图2(a)所示，加装外连接桥、内连接桥、中间连接桥磁性齿轮磁力线分布分别如图2(b)—图2(d)所示。由于图2(a)采用的调磁块的拓扑结构在实际生产制造中机械强度较低，且不便确定各个调磁块之间的相对位置，通常需要在调磁块间加装连接桥。为了确保调磁环具有一定的机械强度，所设计连接桥的厚度不能太薄，为防止内、外转子磁场间的相互屏蔽，所设计连接桥的厚度不能过厚，本次设计连接桥厚度与调磁块厚度之比为2∶15。由图2(a)可见：内转子永磁体所产生的磁力线大多数会穿过调磁块到达外转子，形成闭合磁路。由于外转子永磁体的极矩较小，导致其磁路闭合路径短，所以外转子永磁体所激发的一部分磁力线未到达内转子。由于磁场调制效应，大部分磁力线集中于调磁块上，而相邻空气槽只有少量漏磁通。对比图2(b)—图2(d)可以看出：加装外连接桥对外转子气隙中的磁力线分布有一定影响，而加装内连接桥和中间连接桥分别对内转子气隙磁力线分布和调磁块间隙磁力线分布有一定影响。

图2 调磁块的连接方式

3.2 气隙内磁感应强度分布

内外转子永磁体产生的磁场在内外气隙耦合，由内外转子气隙磁感应强度表达式可以看出，磁场调制型磁性齿轮工作转矩形成的条件为内外转子永磁体产生的谐波具有相同的极对数和转速。不同连接桥对内外转子气隙磁力线分布影响不一，从而使不同设计连接桥下的磁性齿轮具有不同的转矩性能。

4种设计下内转子气隙磁感缨强度分量如图3所示。从图3可以看出：无连接桥时的内转子气隙磁感应强度径向分量大小与采用外连接桥时相当，无连接桥时磁感应强度径向分量最大，加装内连接桥时的则最小；对于切向磁感应强度分量大小，由高到低依次为无连接桥时、外连接桥时、中间连接桥时、内连接桥时；可以得出：加装内连接桥对内转子气隙磁感应强度影响较大，而加装外连接桥对其影响较小。

4种设计下外转子气隙磁感应强度分量如图4所示。从图4可以看出：加装外连接桥对外转子气隙磁感应强度影响较大，而加装内连接桥则对其影响较小，而加装中部连接桥处于内外连接桥大小之间。

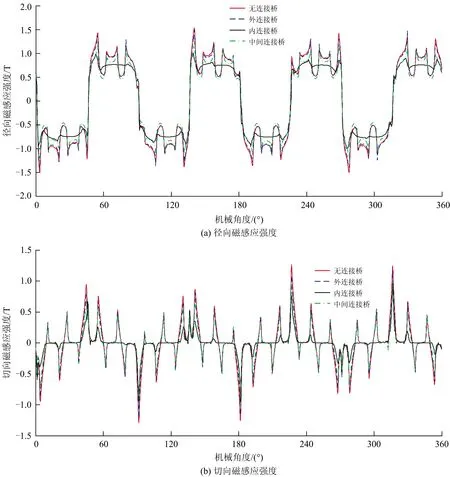
图3 内转子气隙磁感应强度

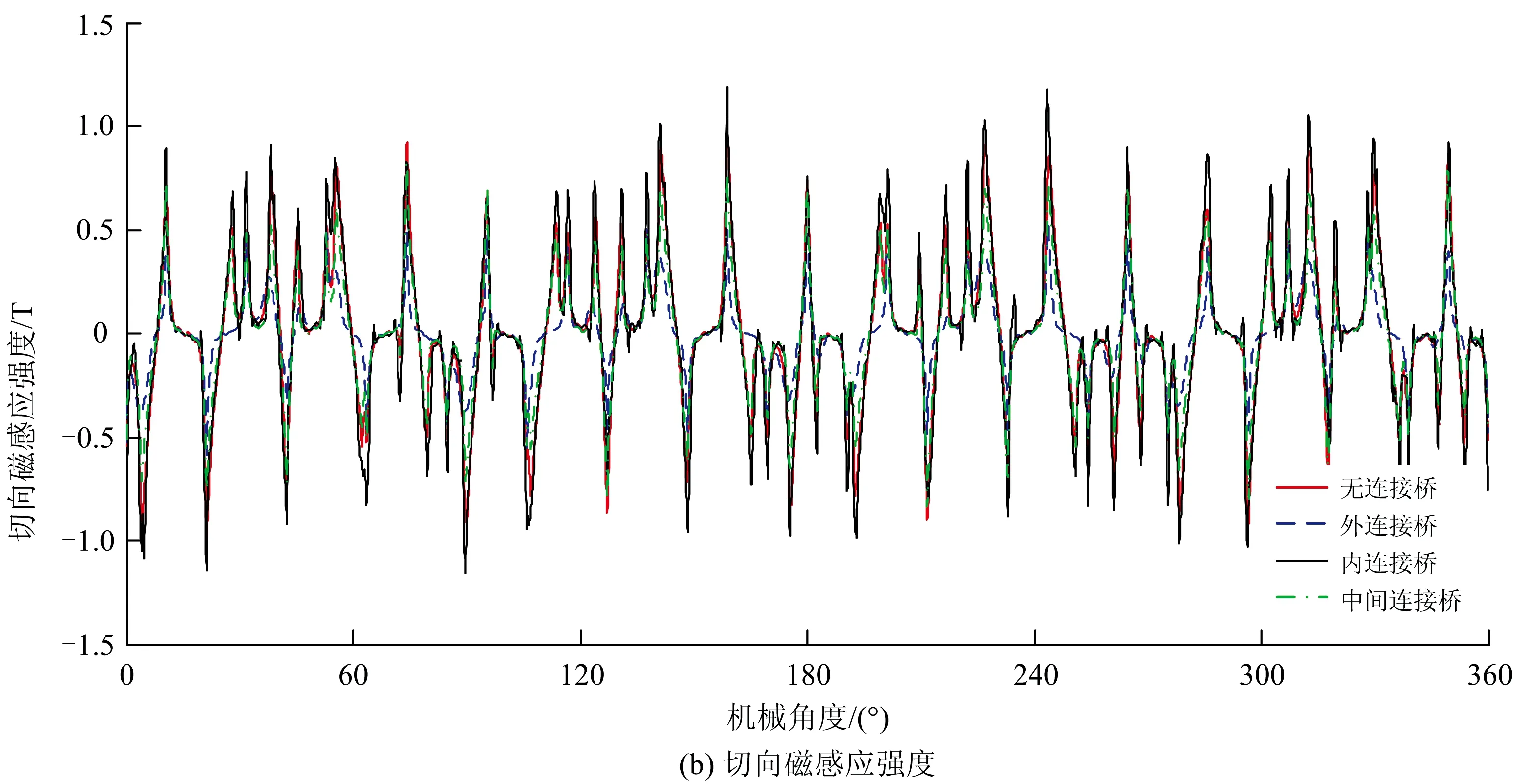
图4 外转子气隙磁感应强度

综合图3和图4可以得出:加装于同侧的连接桥对该侧气隙的磁感应强度有较大影响，而对另一侧的影响较小，采用中间连接桥加装方式的磁感应强度分量大小基本处于加装内、外连接桥之间。

3.3 转子的转矩特性

由内、外转子径向和切向磁感应强度分量与机械角度间的关系图可以直观地观察到采用不同连接方式对其磁感应强度分量的大小的影响。但转矩的大小是通过对气隙中磁场麦克斯韦张量在沿着圆周方向360°进行积分得出，无法直接通过气隙磁感应强度分量的大小来评估磁性齿轮的性能。上文通过解析法得到了外转子最大转矩公式，由式(9)得出外转子最大转矩和外转子气隙径向和切向磁感应强度分量有关。取轴向长度为35 mm，通过Ansoft有限元分析软件对不同角度下外转子转控进行计算，得到转矩—角度曲线如图5所示，具体数值见表1。

通过图7和表1可以看出：与无连接桥时相比，加装连接桥会使磁性齿轮传动性能降低；以无连接桥的外转子峰值转矩为基准，加装外连接桥的峰值转矩仅为基准值的58.1%，而加装内连接桥的转矩峰值为基准值的83.3%，加装中间连接桥的则为基准值的68.3%；采用不同的连接桥加装方式对磁性齿轮峰值转矩产生的影响差别很大，其中采用内连接桥加装方式对磁性齿轮峰值转矩的影响最小，在调磁环实际生产制造中应尽量采用内连接桥加装方式而避免采用中间和外连接桥加装方式。

表1 加转方式与峰值转矩关系

4 结 语

通过解析法给出了无调磁块和引入调磁块的内、外转子气隙磁感应强度分量表达式，对径向磁场调制型磁性齿轮的磁场调制原理进行了阐述。基于调磁块3种不同的连接方式，利用Ansoft有限元分析软件分别对3种连接方式下磁性齿轮的磁感线分布情况，内、外转子气隙径向和切向磁感应强度分量以及外转子转矩进行仿真求解。结果显示：连接桥的加装将使得磁性齿轮气隙间的磁力线分布发生改变，加装于一侧的连接桥将对该侧气隙的磁感应强度分量大小影响较大，而对另一侧气隙的磁感应强度分量影响较小。与无连接桥相比，加装连接桥将使磁性齿轮的传动性能降低，其中加装内连接桥对磁性齿轮峰值转矩影响较小，而加装外连接桥对其影响则较大。在调磁环实际生产制造过程中，为了避免磁性齿轮损失过多的传动性能，应尽量采用内连接桥加装方式。