波形钢腹板曲线箱梁桥静力特性

徐勋 余泓 冉川

（西南交通大学土木工程学院，成都 610031）

与传统的混凝土梁桥相比，波形钢腹板箱梁桥具有自重轻、耐久性好、施工方便的特点，合理利用了混凝土和钢材各自的特性［1］。波形钢腹板曲线箱梁桥在设计时不仅要考虑曲线梁桥纯扭转、翘曲、畸变的影响和弯剪扭耦合效应［2］，还要考虑波形钢腹板自身褶皱效应、正交异性［3］特征。本文结合实际工程，建立不同曲率半径的波形钢腹板曲线箱梁桥模型，分析结构在最不利活载作用下的内力、变形和应力分布变化。同时，结合曲线箱梁桥静力特性的研究［4］，总结腹板形式对曲线箱梁桥静力特性的影响。

1 有限元模型

根据实际工程结构特点，本文采用的计算模型为三跨连续梁，跨径组合为（20+25+20）m，边界条件见图1。横隔板为混凝土材料，端支座处厚0.8 m，中支座处厚1.2 m，在每跨的1/3，2/3处布置0.4 m厚的横隔板［5］。波形钢腹板曲线梁桥横截面布置见图2（a），建立相同布置的混凝土实腹板曲线箱梁桥（图2（b））来对比分析变形和内力。波形钢腹板采用1600型［5］，见图3。

图1 边界条件

图2 横截面（单位：cm）

图3 1600型腹板尺寸大样（单位：mm）

通过ANSYS建立波形钢腹板曲线箱梁桥模型。顶底板以及横隔板混凝土采用8节点的solid45模拟，材料采用普通C40混凝土，弹性模量3.25 GPa，泊松比0.2，质量密度2 400 kg/m3。钢腹板采用4节点的shell63模拟，材料采用Q235钢材，钢材弹性模量2.1 GPa，泊松比0.3，质量密度7.85 g/cm3。由于壳单元和实体单元自由度不同，为了与实际情况吻合，将壳单元嵌入实体单元，并耦合几排公共节点来传递弯矩［6-7］。波形钢腹板曲线梁桥的ANSYS结构离散图如图4所示。

施加荷载为公路-1级车道荷载，车列过桥速度60 km/h。汽车荷载离心力参照JTG D60—2015《公路桥涵设计通用规范》［8］选取，离心力系数为C=V2/（127R），其中V为车速，R为曲率半径。离心力着力点在桥面以上1.2 m。为模拟实际结构的最不利受载情况，荷载按一级汽车荷载双车道布置，外车道外偏2.400 m，内车道内偏0.575 m。本文仅对在活载作用下的结构静力特性进行计算分析，不考虑恒载的影响。

图4 结构离散图

2 内力分析

受曲率的影响，曲线梁内力分析时需要考虑梁内弯矩和扭矩耦合的影响。波形钢腹板曲线箱梁桥在曲线箱梁基础上还需要考虑波形钢腹板的结构特点。本文结合数值模型分析曲线箱梁桥各项参数在最不利活荷载布置下随曲率半径的变化规律。

2.1 支座反力

波形钢腹板曲线梁桥在活载作用下支座反力随曲率半径的变化曲线见图5。可知，支座反力随曲率半径的增加变化明显：①曲率半径为30 m的曲线梁桥逐渐变化为直线桥（R=∞）的过程中，在横向弯矩作用下，端部外侧支座反力减小50.4%，端部内侧支座反力增大83.2%，中支座支反力减小16.5%；②小曲率半径时支反力变化幅度大；③由于端支座和中支座的约束形式不同，中支座支反力受曲率半径的影响远小于端支座。

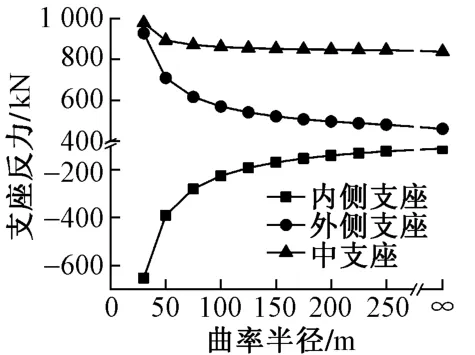
图5 支座反力随曲率半径的变化曲线

2.2 剪力

分别取波形钢腹板曲线箱梁桥边支截面、中支截面和跨中截面最不利荷载情况下的竖向剪力进行分析。各截面在活载作用下剪力随曲率半径的变化曲线见图6。可知：①在R=30 m时，各截面剪力均为负值；②曲率半径为30 m的曲线梁桥逐渐变化为直线桥（R=∞）的过程中，跨中截面剪力减小11.6%，边支截面剪力减小33.3%，中支截面剪应力增大14.3%。

图6 剪力随曲率半径的变化曲线

根据剪力随曲率半径的变化规律可知，存在合适的曲率φ使得曲线桥截面剪力可以近似按直线桥计算。该数值模型在曲率φ≤0.25时，各截面剪力随曲率半径变化的幅度均小于5%，按直线桥计算可以保证足够的精度。

2.3 弯矩

波形钢腹板曲线梁桥竖向弯矩和横向弯矩在最不利荷载布置情况下随曲率半径的变化曲线见图7。

图7 弯矩随曲率半径的变化曲线

由图7可知：①随着曲率半径的增大，跨中截面的竖向正弯矩逐渐增大，中支截面的竖向弯矩逐渐减小，变化幅度分别为34.6%，25.9%。②跨中截面和中支截面的竖向弯矩在曲率φ≤0.25时，变化幅度均小于10%，且随曲率半径的增大竖向弯矩变化平缓。竖向弯矩按直线桥计算，可以满足计算精度要求。③横向弯矩受曲率的影响较大。跨中截面和中支截面横向弯矩均随曲率半径的增大而减小。小曲率半径时，跨中截面在活载作用下横向弯矩最大。

2.4 扭矩

波形钢腹板曲线箱梁桥边支截面、中支截面和跨中截面扭矩随曲率半径变化曲线见图8。

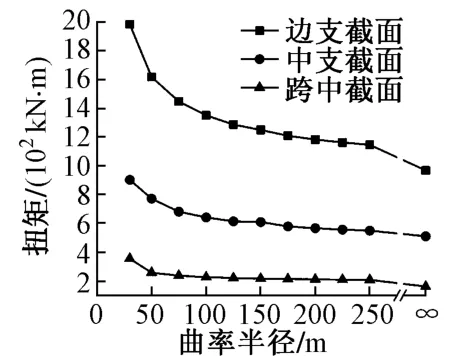
图8 扭矩随曲率半径的变化曲线

由图8可知，曲率半径为30 m的曲线梁桥逐渐变化为直线桥（R=∞）的过程中，各截面的扭矩都有不同程度的减小：边支截面、中支截面和跨中截面的变化幅度分别为42.2%，39.15%和38.8%。桥梁约束的布置形式不同，曲率半径对边支截面扭矩的影响最大，中支截面次之，跨中截面影响最小。

结构曲率、活载的离心力以及活载偏心作用是影响曲线梁桥扭矩的主要因素。波形钢腹板比混凝土实腹板整个截面的抗扭转刚度小很多，导致了在相同荷载作用下扭转变形更加显著。

3 变形分析

仅考虑活载作用，则混凝土箱梁桥和波形钢腹板箱梁桥的内力参数基本相等。在相同荷载作用下，波形钢腹板箱梁桥抵抗变形的能力弱于混凝土箱梁桥。

3.1 挠度

挠度是反映梁结构刚度的重要指标。跨中截面顶板挠度随曲率半径的变化曲线见图9。

图9 挠度随曲率半径的变化曲线

由图9可知，在活载作用下，曲线箱梁桥顶板外侧竖向挠度大于内侧竖向挠度，波形钢腹板箱梁桥顶板竖向挠度大于混凝土箱梁桥同侧顶板的竖向挠度。随着曲率半径的增大，顶板内外侧竖向挠度均呈逐渐减小的趋势。

曲线箱梁桥的挠度主要受竖向弯矩影响，偏心加载是造成顶板内外侧挠度差值的原因。波形钢腹板基本不承担竖向弯矩，仅利用上下混凝土板来抵抗弯矩。在相同荷载作用下，波形钢腹板箱梁桥的挠度大于混凝土箱梁桥同侧竖向挠度，原因是采用波形钢腹板导致箱梁截面竖向刚度发生削减。随着曲率半径的变化，波形钢腹板箱梁桥和混凝土箱梁桥的腹板挠度比值没有发生明显变化。本文实例中，二者的比值保持在1.2。

3.2 翘曲

箱梁在约束扭转时会产生翘曲位移，波形钢腹板曲线梁桥在偏心活载的作用下，弯扭耦合现象更加突出。通过记录同一截面内外侧纵向位移的差值可以反映翘曲的程度。波形钢腹板曲线箱梁桥和混凝土曲线箱梁桥翘曲差值随曲率半径的变化曲线见图10。

图10 翘曲差值随曲率半径的变化曲线

由图10可知：①R=30 m时，波形钢腹板曲线箱梁桥跨中截面顶板翘曲差值为2.469 mm，直线桥时顶板翘曲差值为0.009 mm；②R=30 m时，混凝土曲线箱梁桥跨中截面顶板翘曲差值为1.835 mm，直线桥时顶板翘曲差值为0.004 mm。小曲率半径下，波形钢腹板曲线箱梁桥和混凝土箱梁桥的翘曲差值相差大，直线桥时二者都趋近于0。

曲线箱梁桥中，翘曲主要受横向弯矩和扭矩影响。小曲率半径时，离心力随曲率半径的减小迅速增大，翘曲差值随之增大。与混凝土曲线箱梁桥相比，波形钢腹板曲线箱梁桥抵抗翘曲的能力较弱，曲率半径越小抵抗翘曲变形的能力越弱。

4 应力分析

4.1 正应力

取箱梁的四角点（混凝土顶底板中心线与内外侧腹板的中心线的相交点）作为研究对象，其中LS，LX为内侧的上下角点；WS，WX为其外侧的上下角点。分析时均以角点的应力数值为对象，拉为正，压为负。内力数据分析表明，跨中截面为结构正应力的最不利位置，因而对跨中截面弯矩最大工况进行应力分析。波形钢腹板箱梁桥和混凝土箱梁桥跨中截面正应力分别见图11和图12。

图11 波形钢腹板箱梁桥跨中截面正应力

图12 混凝土箱梁桥跨中截面正应力

由图11和图12可知：①波形钢腹板箱梁桥的正应力分布与混凝土箱梁桥的正应力分布存在差异。②随着曲率半径的增大，波形钢腹板曲线箱梁桥跨中截面的4个角点应力变化趋势不同。角点WX的受拉正应力逐渐减小，角点LX的正应力由受压逐渐变化为受拉，角点WS的正应力由受拉逐渐变化为受压，角点LS的受压正应力逐渐增大。混凝土箱梁跨中截面的4个角点也存在同样的变化趋势。③沿顶底板方向，波形钢腹板箱梁和混凝土箱梁正应力均存在横向分布不均匀的现象，且曲率半径越小分布越不均匀。④沿腹板方向，在钢腹板和混凝土顶底板相交处，应力集中现象明显，正应力发生了突变。曲率半径越小突变程度越大。

研究箱梁截面应力时，忽略了畸变、剪力滞后、剪切变形对翘曲应力的削减作用［4］，仅探究正应力成分中翘曲应力和弯曲应力沿曲率半径的变化规律。本文选择角点WX（最大拉应力点）的各应力成分为研究对象，对比波形钢腹板箱梁桥和混凝土箱梁桥翘曲应力占主应力的比例随曲率半径的变化规律，分别见表1和表2。

表1 波形钢腹板箱梁桥应力成分

由表1和表2可知，波形钢腹板曲线箱梁桥翘曲应力σω及其占正应力的比例（σω/σ）均大于混凝土曲线箱梁桥，这种现象在小曲率半径时更明显。因此，在波形钢腹板曲线箱梁桥的结构设计中，需要注意因扭转和畸变而产生的纵向翘曲应力。

表2 混凝土箱梁桥应力成分

4.2 钢腹板剪应力

已有理论和实验研究表明，波形钢腹板主要承受剪力，且钢腹板的剪应力远大于混凝土箱梁的腹板剪应力。波形钢腹板直线箱梁桥在对称荷载作用下，腹板剪应力沿腹板高度均匀分布［9-11］。在最不利活载作用下，箱梁跨中截面内外侧波形钢腹板剪应力变化曲线见图13。

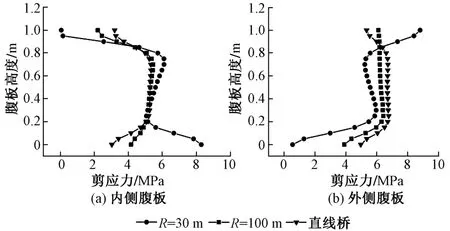
图13 波形钢腹板剪应力变化曲线

由图13可知：①直线桥时，在最不利活载作用下，腹板靠近顶底板一定范围内的剪应力小于腹板中部剪应力，腹板中部剪应力均匀分布。②曲线桥时，随着曲率半径的减小，离心力逐渐增大，扭转效应更明显。内侧腹板上端剪应力逐渐减小，下端剪应力逐渐增大；外侧腹板上端剪应力逐渐增大，下端剪应力逐渐减小。③随着曲率半径的减小，混凝土顶底板和波形钢腹板相交处剪应力变化会更加剧烈，曲率半径足够小时，最大剪应力出现在相交处。

5 结论

1）波形钢腹板曲线箱梁桥的支座反力、剪力、弯矩、扭矩等内力参数随曲率半径的增大越发趋向于直线桥的受力特点。当曲率小于合适的值时，曲线桥可以用相应的直线桥内力参数近似计算。

2）影响曲线箱梁桥挠度的主要内力因素是竖向弯矩；在活载作用下波形钢腹板曲线箱梁桥顶板竖向挠度大于混凝土曲线箱梁桥同侧顶板的竖向挠度。

3）与混凝土曲线箱梁桥相比，波形钢腹板箱梁桥抵抗翘曲变形的能力弱，翘曲应力占正应力的比例大。

4）与混凝土曲线箱梁桥相比，波形钢腹板曲线箱梁桥顶底板的正应力横向分布更加不均匀，且曲率半径越小不均匀现象越明显。顶底板和波形钢腹板相交处存在应力集中现象。

5）最不利活载作用下，波形钢腹板曲线箱梁桥腹板剪应力沿腹板高度分布不均匀，且曲率半径越小不均匀现象越明显。曲率半径足够小时最大剪应力出现在波形钢腹板与混凝土顶底板相交处。