钢筋混凝土梁疲劳性能的有限元分析

赵体波

（中国铁道科学研究院集团有限公司高速铁路轨道技术国家重点实验室，北京 100081）

钢筋混凝土结构一般作为静力承载构件，但在实际工程应用中（如公路桥梁、铁路桥梁、吊车梁等结构）常常受到变幅荷载的作用。随着交通及运输量的日益剧增，既有钢筋混凝土结构长期承受疲劳荷载的反复作用，其承载力随着疲劳损伤的累积而逐渐退化直至结构失效，导致结构在未达到静力承载极限的状态下发生疲劳破坏［1］。为了确保梁结构的运营安全，为结构加固、限载或拆除重建提供技术依据，需要对钢筋混凝土结构的疲劳性能和疲劳寿命进行分析。

已有研究表明，由于结构承受的疲劳荷载一般远小于结构的静力极限承载力，适筋钢筋混凝土梁的受压区混凝土不是引起结构疲劳破坏的原因［2-3］，然而受压区混凝土在循环荷载作用下变形模量发生退化，残余应变逐渐累积，从而影响结构整体的疲劳性能。钢筋混凝土梁的疲劳破坏通常由梁中纵向受拉钢筋的疲劳断裂导致，因此对工程中常用的变形钢筋的疲劳性能展开了大量研究［4-5］。

以往主要通过疲劳试验来研究钢筋混凝土梁的疲劳性能，然而疲劳试验存在费用昂贵且容易受到试验条件影响等缺点［6］。近年来数值模拟分析方法在结构计算研究领域得到了快速发展，通过有限元方法进行计算分析已是研究结构受力性能的重要手段［7］。大型通用有限元软件ABAQUS是其中具有代表性的软件之一，因其在非线性分析方面具有巨大优势，在混凝土结构分析中得到了广泛的应用［8］。本文基于有限元软件ABAQUS和疲劳分析软件FE⁃SAFE，结合混凝土和钢筋的应力-疲劳寿命模型，对钢筋混凝土的疲劳性能进行分析，并对不同混凝土强度和不同配筋率钢筋混凝土梁的疲劳性能进行对比。

1 基于ABAQUS的静载受力分析

1.1 模型梁

本文钢筋混凝土梁的截面形式及配筋情况如图1所示，模型中采用的混凝土和钢筋的基本力学性能分别见表1和表2。其中，P为集中荷载。

图1 模型梁结构配筋示意（单位：mm）

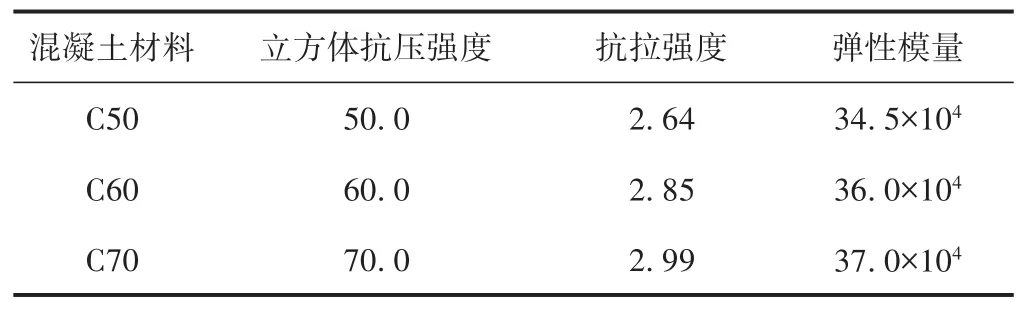
表1 混凝土材料基本力学性能 MPa

表2 钢筋力学性能 MPa

钢筋混凝土梁在疲劳荷载作用下的性能发展过程较为复杂，影响其疲劳寿命的因素较多，主要包括混凝土强度、纵向钢筋配筋率、荷载水平、几何尺寸、加载频率等。虽然实际使用中结构受到的是随机变幅荷载，但为方便研究，目前对钢筋混凝土梁疲劳性能的研究仍以施加等幅疲劳荷载为主。

本文主要研究混凝土强度等级、钢筋强度等级、钢筋配筋率和疲劳荷载水平对钢筋混凝土梁疲劳性能的影响。通过有限元软件ABAQUS建立了8根具有不同混凝土强度等级、不同钢筋等级和不同配筋率的钢筋混凝土梁的有限元模型，模型梁试验参数见表3。其中，Pmax为疲劳上限荷载；Pmin为疲劳下限荷载；Pu为静力极限承载力。

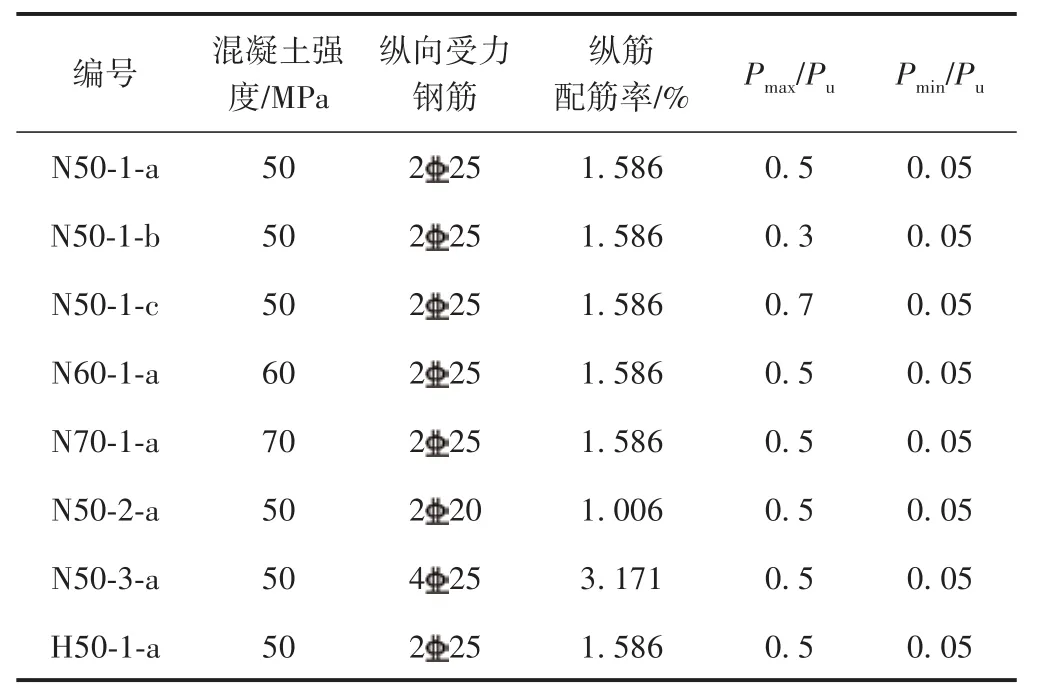
表3 模型梁试验及参数

1.2 基于ABAQUS的有限元分析

本文中混凝土采用三维六面体减缩单元C3D8R模拟，采用混凝土塑性损伤模型，纵筋和箍筋采用两结点线性三维桁架单元T3D2模拟，建模时对混凝土和钢筋骨架采用分离式嵌入模型。为避免加载时梁体出现应力集中，加载垫板和支座材料均采用弹性钢垫块。混凝土梁的加载形式为两点加载，梁N50⁃1有限元计算结果梁如图2所示。

图2 梁N50⁃1有限元计算结果

2 基于ABAQUS/FE⁃SAFE的疲劳性能分析

FE⁃SAFE可以利用名义应力法、局部应力-应变法、能量法、场强法等方法对结构进行单轴或多轴载荷的疲劳特性分析，针对实际工程中混凝土梁结构高周低幅的受力情况，对钢筋混凝土梁采用应力-寿命法能获得更好的疲劳寿命预测精度。

2.1 材料损伤准则

工程上常用的损伤模型有主应变准则、最大剪应变准则和 Brown⁃Miller准则。其中 Brown⁃Miller准则是1973年Brown M W和Miller K J提出的疲劳理论［9］，认为裂纹的产生发生在最大剪应变所在的特定平面，其对延性金属材料的寿命估计与实际最相符，因此本文对钢筋的疲劳分析采用Brown⁃Miller准则。普通混凝土属于脆性材料，无论是受压区还是受拉区混凝土的受力情况均近似于单轴受力状态，其疲劳分析一般选用Goodman准则。混凝土材料的表面比较粗糙，光滑度大于75 μm，钢筋表面的光滑度设置为Machined。

2.2 基于FE⁃SAFE的疲劳性能分析

提取ABAQUS中的应力-应变分析结果，导入FE⁃SAFE中进行疲劳分析，采用等幅正弦荷载形式，加载频率为2 Hz。以静力分析结果为基础，分别对混凝土梁施加不同等级的疲劳荷载，梁N50⁃1⁃a中混凝土和纵向钢筋的疲劳寿命云图如图3所示。

图3 梁N50⁃1⁃a钢筋和混凝土对数疲劳寿命云图（单位：次）

从图3（a）可知，受压区普通混凝土在1 000万次疲劳荷载作用下未出现受压疲劳破坏，这是由于在疲劳荷载作用下受压区混凝土应力水平较低，受压区混凝土仍处于弹性阶段，因此表现出较高的抗疲劳性能［10-11］。而受拉区混凝土在初次荷载作用下即发生开裂，当循环加载至104～105数量级时，剪跨段内的裂缝继续向支座位置扩展，纯弯段内的裂缝进一步向上延伸。从图3（b）可知，梁底纵向钢筋的疲劳寿命约为153万次，梁N50⁃1⁃a的疲劳破坏是由钢筋的疲劳失效引起的。以上有限元分析结果与钢筋混凝土实梁的疲劳裂缝发展特点以及疲劳破坏形式基本一致［12-13］。

3 钢筋混凝土梁疲劳性能影响因素

本文研究不同混凝土强度等级、不同配筋率的钢筋混凝土梁在不同疲劳荷载作用下的疲劳寿命，结果见表4。

表4 钢筋混凝土梁疲劳寿命

从表4可知，疲劳最大荷载水平对疲劳寿命的影响非常明显，梁的抗弯疲劳寿命随荷载水平的升高有显著的降低。提高混凝土强度可以提高梁的抗弯疲劳寿命，梁N50⁃1⁃a的疲劳寿命为1 527 566次，当混凝土强度提高至C60时，梁的疲劳寿命增长至3 481 612次，继续提高混凝土强度至C70，梁的疲劳寿命为2 476 856次，由此可以发现，在一定范围内提高混凝土强度可以增加梁的抗弯疲劳寿命，然而过高的混凝土强度使梁的疲劳寿命提高幅度有所下降。钢筋混凝土梁的疲劳寿命随着配筋率的增加而增大，原因是随着配筋率的增加，达到同一荷载水平时截面受拉区开裂较小，钢筋周围混凝土的塑化作用增大，即配筋率的增大间接提高了混凝土的抗拉疲劳强度，受拉区混凝土的贡献增大，钢筋的疲劳应力水平有所降低，梁的整体疲劳寿命得到提高。

4 结论

1）本文通过有限元软件ABAQUS模拟了钢筋混凝土梁在静力荷载下的受力过程，并通过疲劳计算软件FE⁃SAFE对钢筋混凝土梁的疲劳性能进行分析，得到混凝土梁全结构疲劳寿命云图，根据ABAQUS/FE⁃SAFE分析得到的钢筋混凝土梁的疲劳发展过程与试验中混凝土梁的疲劳性能发展特点相吻合。

2）疲劳荷载水平对钢筋混凝土梁的疲劳寿命影响较大，梁的抗弯疲劳寿命随荷载水平的提高显著降低；配筋率较高的钢筋混凝土梁中受拉区混凝土的抗拉疲劳性能可以得到相对更为充分的利用，因此梁的抗弯疲劳寿命随配筋率的提高而增大；在一定范围内提高混凝土强度可以显著提高梁的疲劳寿命，超过这一范围后继续增强混凝土强度，梁的疲劳寿命提高幅度反而有所降低。

3）由于ABAQUS/FE⁃SAFE的计算中未准确考虑钢筋与混凝土之间的黏结滑移影响以及结构疲劳退化过程中的应力重分布，使得文中的有限元计算模拟与实际情况存在差别，因此在疲劳寿命的模拟计算方面还需要进一步研究。