点差法解圆锥曲线中点弦问题新发现

广东省中山市第一中学 (528403) 李 虎

一、问题提出

此题的结论是没有.常用的做法有两种，一种是联立方程利用韦达定理及中点坐标公式结合判别式得出结论；另一种是利用点差法.点差法计算量小，但是面临验证是否有交点的问题，在练习题评讲过程中学生也提出为什么要验证？求出的直线又是什么呢？在课堂上，笔者从逻辑推理的角度给学生作了错误原因的分析.课后笔者也查找了文献，文[1][2]中把这种问题的原因归结于其共轭双曲线，笔者认为原因不在于此，并找出了此直线的真实含义.文[1][3][4][5]对点满足什么样的条件，这样的直线存在做了研究，为快速判断这样的直线是否存在奠定了基础.

二、逻辑推理过程中找原因

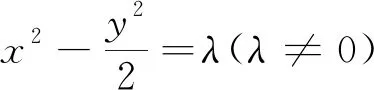
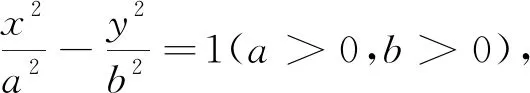
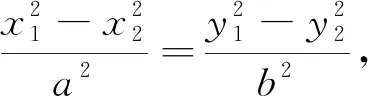
注1：这样就解释了为什么任给一个不在渐近线上的点都可以用点差法求出一条直线，这条直线是相对于“与已知双曲线共渐近线的双曲线系”来说的，所以要判断所求直线是否与已知的双曲线是否相交.

注2：文献[3]中已经证明当点p位于渐近线与双曲线所围成的区域内时(包含渐近线和曲线本身)，不存在以p为中点的弦，其余区域存在以p为中点的弦.

三、知识迁移

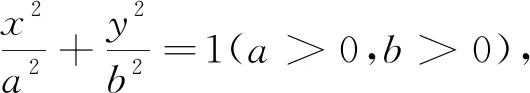
证明方法与双曲线类似，这里不再赘述.

任给平面一点，针对椭圆也可以用点差法求出一条直线，这条直线是相对于“共离心率的椭圆系”方程来说的.对给定的椭圆，容易知道，若所给的点在已知椭圆上或椭圆外，那么不会存在以这个点为中点的弦，若所给的点在椭圆的内部，则存在以p点为中点的弦.考题所给的点都在椭圆内，所以给大家一种椭圆方程用点差法解决中点弦问题不用验证判别式的错觉.

结论3 已知抛物线y2=2px(p>0)，对平面内任意一点P(x0,y0)，则存在实数λ使得P(x0,y0)是抛物线y2=2px+λ中某一条弦AB的中点.

任给平面内一点，针对抛物线也可以用点差法求出一条直线，这条直线是相对于“共对称轴的抛物线系”来说的.容易知道，若这个点在抛物线所围起焦点所在的一侧，以p点为中点的弦存在，反之，在抛物线上，或者在抛物线的另一侧，那么这种弦不存在.

四、结束语

点差法处理中点弦问题有很多优点，体现了数学的简洁美，同时也体现了事物的广泛联系性，中点的坐标就这样和斜率产生了关系.通过本题的探究有助于学生推理严密性的培养，同时也可以培养学生从多个角度看问题，思考问题，解决问题，拓展思维的宽度和深度.