高考函数“依式选图”问题求解策略*

甘肃省武威第十六中学 (733018) 刘玉文

因为函数图象是高中数学的重要基础，所以函数图象一直是历年高考选择题的命题热点.高考函数图象选择题的类型有“依式选图”和“依图选图”两类.依式选图是指根据函数解析式选择函数图象选项；依图选图是指根据图象或图形选择函数图象选项.其中“依式选图”问题一直是历年高考选择题的常考题型，它能很好地考察函数图象性质的综合运用，解法灵活多样,具有直观性、基础性、灵活性和综合性的特点，是体现数形结合思想的典范，培养核心素养的良好素材.作者对近几年来高考函数“依式选图”选择题进行了归纳、比较与分析，并选其具有代表性的典型试题的解题策略进行展示，以期达到抛砖引玉之功效.

1.直接法

直接由函数解析式确定函数的定义域、值域及函数的单调性、奇偶性、周期性等性质，再根据这些性质对函数图象进行具体分析判断，然后对照题目所给出的选项“对号入座”，做出相应的选择.直接法的解题过程，实质就是数学核心素养的提升和展示过程.

例1 (2018浙江理)函数y=2|x|sin2x的图像可能是( ).

解析：令y=f(x)=2|x|sin2x，则f(-x)=2|-x|sin(-2x)=-2|x|sin2x=-f(x),所以f(x)为奇函数①；当x∈(0,π)时，2|x|>0,sin2x可正可负，所以f(x)可正可负②.由①②可知,选D.

评注：(1)运用函数性质研究函数图像时，先要正确理解和把握函数相关性质本身的含义及其应用方向.(2)在运用函数性质特别是奇偶性、周期性、对称性、单调性、最值、零点时，要注意用好其与条件的相互关系，结合特征进行等价转化研究.如奇偶性可实现自变量正负转化，周期性可实现自变量大小转化，单调性可实现将函数值的大小转化自变量大小关系.

2.特例法

在解选择题时，可以通过取一些特殊数值、特殊点、特殊位置、特殊函数等对选项进行验证，从而可以否定和排除不符合题目要求的选项，得到正确的选项，这就是特殊化策略在解选择题中的应用.

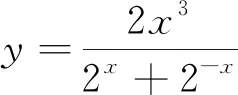
评注：本题通过判断函数的奇偶性，排除错误选项，通过计算特殊函数值，作出选择．考察了逻辑推理、数据分析和数学运算素养.特殊数值、特殊点、特殊位置、特殊范围是一举突破这类问题的最佳思路.用特例法解题时要注意：(1)所选取的特例一定要简单，且符合题设条件；(2)特殊只能否定一般，不能肯定一般；(3)当选取某一特例出现两个或两个以上的选项都正确时，这时要根据题设要求选择另外的特例代入检验，直到找到正确选项为止.

3.排除法

充分运用选择题中单选的特征(有且只有一个正确选项)，通过分析、推理、计算、判断，逐一排除，最终得出正确选择.

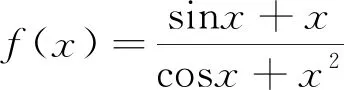
评注：本题考查函数的性质与图像，渗透了逻辑推理、直观想象、数据分析和数学运算素养.解答本题时，先判断函数的奇偶性，得f(x)是奇函数，排除A，再注意到选项的区别，利用特殊值得正确答案．排除法适用于不易直接求解的选择题.当题目中的选项多于一个时，先根据某些条件在选项中找出矛盾，这样逐步排除，直到得出正确的选项.它与特例法、图解法等结合使用是解选择题的常用而有效的方法.

4.分类讨论法

在解答某些数学问题时，有时会有多种情况，对各种情况加以分类，并逐类求解，然后综合求解，这就是分类讨论法.它能很好地训练学生思维的条理性和概括性，培养学生逻辑推理、数学抽象等素养，所以在高考试题中占有重要的位置.

评注：本题易出现的两个错误：一是指数函数、对数函数的图像和性质掌握不熟练，导致判断失误；二是不能通过讨论a的不同取值范围，认识函数的单调性.分类讨论是一种逻辑方法，也是一种数学思想.分类时注意：分类的对象是确定的，标准是统一的，不遗漏、不重复、分层次，不越级讨论.

5.导函数定性法

当遇到比较复杂的函数解析式时，函数的单调性不能直接进行判断，此时可借助导数工具，利用导函数的符号来判断.但要注意函数求导之后，解析式发生了变化，故导函数的定义域与原函数的定义域可能有所不同，但必须在原函数的定义域内研究函数的单调性.

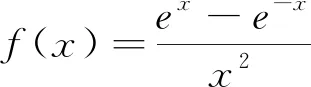
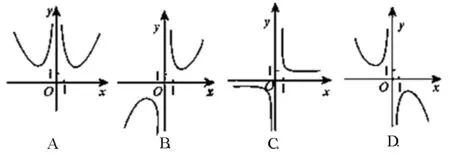
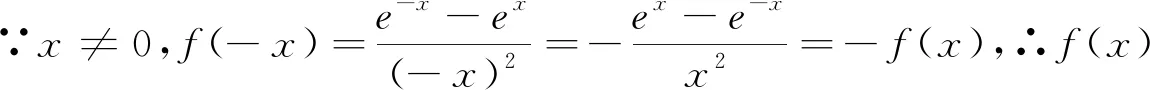
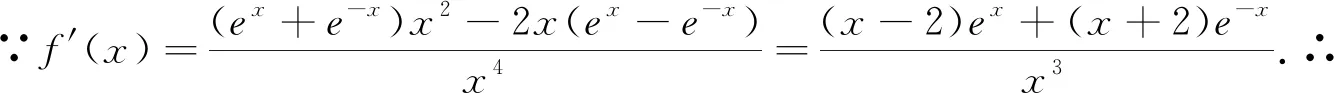
评注：本题根据解析式的结构特征，通过研究函数奇偶性以及单调性，确定函数的图像.本题的解答，很好地考察了数学抽象、逻辑推理、直观想象和数学运算等核心素养.

6.图象变化趋势法

当函数的符号变化不易判断时，应从函数图像的变化——包括函数的单调性、奇偶性、函数在区间上的零点以及最值变化等角度，深入分析函数图像的变化趋势，来判断函数的图像.

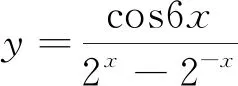
解析：由三角函数的有界性，可知cos6x∈

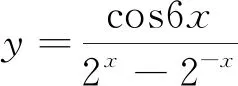
总之，高考函数“依式选图”选择题的解答，要结合已知解析式和选项灵活处理.根据解析式研究函数的有关性质，并对图像在坐标系中的位置和图像的变化趋势进行具体分析判断，找出选项之间的不同，准确进行验证排除，进而可得正确选项.这样，不仅使问题迎刃而解，而且使学生的数学核心素养得到有力提升.