蜗杆砂轮磨齿机几何误差敏感度分析

陶小会，李国龙，徐 凯，李传珍

（重庆大学机械传动国家重点实验室，重庆400044）

随着制造业的快速发展，对数控机床加工精度的要求越来越高。影响数控机床加工精度的因素包括几何误差、热误差、力误差和伺服误差等，其中几何误差所占比例较高。提高数控机床加工精度的方法有精度设计和误差补偿［1］，但蜗杆砂轮磨齿机等机床的结构复杂，误差种类多，盲目进行精度设计和误差补偿的成本高、效率低且难以取得较好的效果。因此，通过建立机床几何误差模型，识别影响机床空间精度的关键几何误差项，对机床精度设计和误差补偿有理论指导意义。

常用的机床几何误差建模理论包括多体系统理论［2-4］、刚体运动学理论［5］和齐次坐标变换理论［6-8］等，但基于上述理论的几何误差建模过程较复杂，需要在每个运动轴上建立局部坐标系。旋量理论［9-10］可以在全局坐标系下描述刚体运动，简化了建模过程，被广泛应用于机器人领域，但较少用于机床运动学建模。对于几何误差的敏感度分析，国内外许多学者进行了研究，例如：黄强等［11］对影响滚齿机加工精度的关键误差源进行了识别；程强等［12］利用矩阵微分法识别出机床的关键几何误差；Chen等［13］利用矩阵微分法对五轴数控机床的37个几何误差进行了敏感度分析；Cheng等［14］基于Sobol法识别了立式加工中心的关键几何误差；Zou 等［15］采用基于方差的敏感度分析方法，研究了三轴金刚石车床中每个误差源对加工误差的影响；廖琳［16］利用敏感度分析理论分析了影响机床姿态误差的主要几何误差；Guo等［17］通过扩展傅里叶振幅敏感度测试（extended Fourier amplitude sensitivity test，EFAST）法确定了每个几何误差对机床空间精度的影响；Cheng等［18］提出了一种基于指数螺旋理论和Morris 法的误差敏感度分析方法，并将它用于机床加工精度全局敏感度分析；夏长久等［19］建立了几何误差-齿面误差模型，并基于Morris法识别了影响磨齿机精度的关键几何误差。综上所述，目前几何误差敏感度研究主要针对通用机床，而较少关注蜗杆砂轮磨齿机。

为此，笔者提出一种基于旋量理论和Sobol法的蜗杆砂轮磨齿机几何误差敏感度分析方法。首先，基于旋量理论建立蜗杆砂轮磨齿机几何误差模型；然后，采用Sobol法对蜗杆砂轮磨齿机磨削过程进行几何误差敏感度分析；最后，修正蜗杆砂轮齿磨机的关键几何误差项，通过仿真分析对比修正前后机床的空间误差分量和3种测量模式下球杆仪的杆长，以验证敏感度分析结果的正确性和有效性。

1 蜗杆砂轮磨齿机几何误差建模

1.1 旋量理论

根据Chasles定理，任意刚体的运动都可以通过绕某一轴的转动加上沿该轴的移动来实现，该组合运动称为旋量运动。假设运动旋量，其中为旋转方向的单位向量为移动方向的单位向量，运动位移为θ，则刚体运动变换矩阵可以用运动旋量的指数表示：

式中：

对于平动轴，当w = 0时，有：

对于旋转轴，当w ≠0时，有：

运动链中的刚体经过一定转动和移动之后，第n个刚体相对于基座标系的运动变换矩阵可表示为：

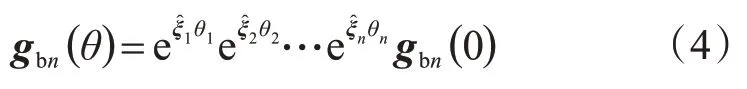
式中：gbn(0)为初始位置时第n 个刚体相对于基座标系 的 运 动 变 换 矩 阵；ξi(i = 1，2，…，n) 和θi(i =1，2，…，n)分别表示第i 个刚体的运动旋量和运动位移。

1.2 蜗杆砂轮磨齿机几何误差分析

YW7232 型蜗杆砂轮磨齿机如图1 所示。由于制造缺陷和装配误差，蜗杆砂轮磨齿机工作时会产生几何误差，这些几何误差可分为位置相关几何误差和位置无关几何误差。蜗杆砂轮磨齿机有3个直线轴（X 轴、Y 轴、Z 轴）和3 个旋转轴（A 轴、B 轴、C 轴），其中：B轴为电主轴，精度高，可忽略其几何误差；其余每轴运动时均会产生6 项位置相关几何误差。以X轴为例，X 轴运动时会产生沿X 方向的定位误差δx(x)，滚转误差εx(x)，沿Y、Z 方向的直线度误差δy(x)、δz(x)，俯仰误差εy(x) 以及偏转误差εz(x)。同时，蜗杆砂轮磨齿机还存在11项位置无关几何误差，包括直线轴间的3项垂直度误差（φzy、φxy、φxz）以及旋转轴的8项安装误差（δya、δza、φya、φza、δxc、δyc、φxc、φyc）。综上，蜗杆砂轮磨齿机共有41项几何误差，具体误差项及对应编号如表1所示。

1.3 基于旋量理论的几何误差建模

蜗杆砂轮磨齿机的拓扑结构如图2所示，主要由2 个分支组成：刀具分支和工件分支。其中，刀具分支由机床床身、X轴、Z轴、A轴、Y轴、B轴和刀具组成；工件分支由机床床身、C轴和工件组成。

蜗杆砂轮磨齿机有3个移动轴和3个旋转轴，理想情况下，机床的旋量运动为沿X轴移动x、沿Y轴移动y、沿Z 轴移动z、绕A 轴转动角度a、绕B 轴转动角度b、绕C轴转动角度c。以A轴为例分析误差运动旋量，A轴的位置无关几何误差运动可以用2组旋量运动表示：沿Y轴移动δya，绕Y轴转动角度φya，记为ξeya；沿Z 轴移动δza，绕Z 轴转动角度φza，记为ξeza。A 轴的位置相关几何误差运动可以用3组旋量运动表示：沿X 轴移动δx(a)，绕X 轴转动角度εx(a)，记为ξex(a)；沿Y轴移动δy(a)，绕Y 轴转动角度εy(a)，记为ξey(a)；沿Z 轴移动δz(a)，绕Z轴转动角度εz(a)，记为ξez(a)。蜗杆砂轮磨齿机各轴的理想运动旋量ξij和误差运动旋量ξej如表2所示，其中j = x，y，z，a，b，c。

图1 YW7232型蜗杆砂轮磨齿机示意图Fig. 1 Schematic diagram of YW7232 worm wheel gear grinding machine

表1 蜗杆砂轮磨齿机几何误差及对应编号Table 1 Geometric errors and corresponding numbers of worm wheel gear grinding machine

图2 蜗杆砂轮磨齿机拓扑结构Fig. 2 Topology structure of worm wheel gear grinding machine

由旋量理论可知，工件相对于机床的运动变换矩阵可表示为：

刀具相对于机床的运动变换矩阵可表示为：

则刀具相对于工件的运动变换矩阵为：

理想情况下，刀具相对于工件的运动变换矩阵为：

式中：θji表示理想情况下j轴的运动位移表示理想情况下j轴的运动变换矩阵。

实际情况下，刀具相对于工件的运动变换矩阵为：

式中：θjr表示实际情况下j轴的运动位移；eξ^jrθjr表示实际情况下j轴的运动变换矩阵，以A轴为例，实际情况下A轴的运动变换矩阵

则误差矩阵E可表示为：

表2 蜗杆砂轮磨齿机各轴的运动旋量Table 2 Motion screw of each axis of worm wheel gear grinding machine

基于六自由度理论和小误差假设理论，E又可表示为：

式中：Δx、Δy、Δz，Δα、Δβ、Δγ 分别表示刀具相对于工件沿X、Y、Z方向的位置误差分量和角度误差分量，统称为空间误差分量。

2 蜗杆砂轮磨齿机几何误差敏感度系数计算

2.1 Sobol法

Sobol法是基于方差分解的改进蒙特卡洛方法。采用Sobol 法对模型Y =f (x)进行敏感度分析，其中x=(x1，x2，…，xl)表示l个输入参数。在蜗杆砂轮磨齿机几何误差敏感度分析中，以X方向的位置误差分量Δx为例进行分析，Δx与几何误差的关系可表示为：

式中：e = (e1，e2，…，e41)，表示输入的41项几何误差。

根据Sobol 法的基本原理，对式（12）进行分解，可得：

式中：Δx0是基于输入量的X方向的位置误差分量Δx的期望值，为常数；Δxp(ep)表示输入量ep作用下对应的X方向的位置误差分量；Δxp，q(ep，eq)表示输入量ep和eq共同作用下对应的X方向的位置误差分量，其余高阶项以此类推。

式（12）所示模型输出项的总方差和偏方差分别为：

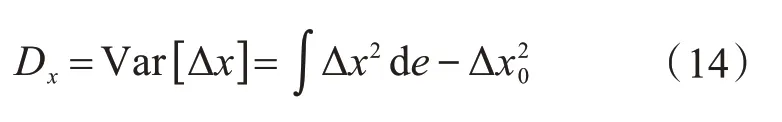
式中：1≤s ≤41。

总方差可分解为：

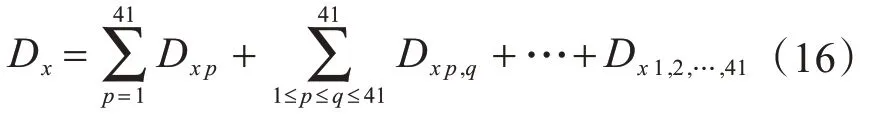
令：

式（16）左右两边同时除以Dx，可得：

式中：Sxp是输入量ep对X 方向位置误差分量的一阶敏感度系数，表示单个几何误差对X方向位置误差分量的影响；Sxp，q是输入量ep和eq对X方向位置误差分量的二阶敏感度系数，表示ep和eq共同作用对X位置误差分量的影响；其余高阶项同理。

在进行蜗杆砂轮磨齿机几何误差敏感度分析时，通常只分析其一阶敏感度和全局敏感度，则输入量ep对X方向位置误差分量的一阶敏感度系数可表示为：

输入量ep对X方向位置误差分量的全局敏感度系数可表示为：

其中：

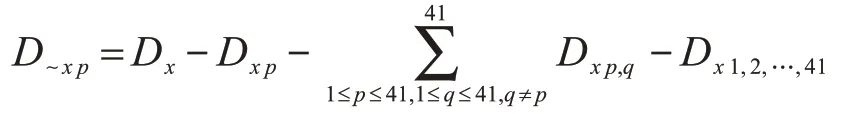
2.2 蒙特卡洛估算

在计算蜗杆砂轮磨齿机几何误差对空间误差分量的敏感度系数前，需通过蒙特卡洛采样方法对输入参数进行采样，生成2个相对独立的采样矩阵。仍以X方向的位置误差分量Δx为例进行分析，其期望值、方差、偏方差、D～xp的估算公式为：

式中：k代表每个输入量的采样个数；上标(1)，(2)表示2个采样矩阵的编号；Gm表示从采样空间取得的第m个采样集；gpm表示采样点集中第m个采样点的第p个几何误差的值。

将式（21）至（24）代入式（19）、（20）中，即可计算出蜗杆砂轮磨齿机几何误差对X方向位置误差分量的一阶敏感度系数和全局敏感度系数。

3 蜗杆砂轮磨齿机几何误差敏感度分析实例

3.1 指令位置分析及几何误差采样

蜗杆砂轮磨齿机为专用机床，磨削齿轮时其运动轨迹单一。以YW7232型蜗杆砂轮磨齿机为研究对象，分析其磨削过程中各几何误差对空间误差分量的敏感度。

蜗杆砂轮磨齿机磨削齿轮时，齿轮参数和蜗杆砂轮参数如表3所示，其中，齿轮和砂轮的旋向均为右旋。蜗杆砂轮磨削运动包括4个运动过程：砂轮和齿轮的旋转运动、砂轮径向进给运动、砂轮轴向冲程运动和砂轮窜刀运动。在磨削之前，蜗杆砂轮磨齿机B轴和C轴的初始角度为0°，A轴旋转角度由齿轮和砂轮的螺旋角确定；在磨削过程中，X轴进给到指定位置后保持静止，Y 轴和A 轴静止不动，由B 轴、C 轴和Z轴联动完成磨削过程。B轴、C轴的转动角度以及Z轴的位置都与时间t有关：

表3 齿轮和蜗杆砂轮参数Table 3 Parameters of gear and worm wheel

根据经验，取x = 260 mm，z0= 280 mm，假定Y轴在单次磨削过程中保持静止，但为了保证砂轮能在整个刀具长度方向被充分利用，在多次磨削后砂轮会发生沿Y 轴的窜刀运动，因此分别对y =-60，- 20，20，60 mm，t = 0，4，8，12，16，20 s 时对应的24个机床指令位置处的几何误差项对空间误差分量的敏感度进行分析。

使用Renishaw XL-80激光干涉仪和QC20-W球杆仪对蜗杆砂轮磨齿机进行多次重复实验，测得机床的几何误差范围，对该范围进行合理缩放后得到：位置误差范围为0～20 μm，角度误差范围为0''～10''，且几何误差元素符合正态分布。

3.2 敏感度分析结果

分别计算24个指令位置处各几何误差项对Δx、Δy、Δz、Δα、Δβ、Δγ 的一阶敏感度系数和全局敏感度系数，再通过式（25）和式（26）对24 个指令位置处的敏感度系数求平均数，可以得到机床磨削过程中各几何误差项对空间误差分量的敏感度系数，结果如图3至图8所示。

式中：Sp和STp分别表示第p项几何误差的一阶敏感度和全局敏感度系数，Shp和SThp分别表示第p项几何误差在位置h处的一阶敏感度系数和全局敏感度系数。

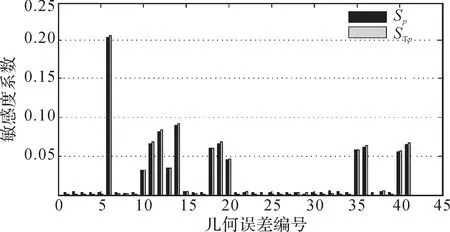
图3 YW7232型蜗杆砂轮磨齿机几何误差对X 方向位置误差分量的敏感度系数Fig. 3 Sensitivity coefficient of geometric errors to X-direction position error component of YW7232 worm wheel gear grinding machine

图4 YW7232 型蜗杆砂轮磨齿机几何误差对Y 方向位置误差分量的敏感度系数Fig. 4 Sensitivity coefficient of geometric errors to Y-direction position error component of YW7232 worm wheel gear grinding machine

基于以上一阶敏感度系数以及全局敏感度系数计算结果，可以得出如下结论：

1）将敏感度系数大于0.05的几何误差项作为关键几何误差项，根据图3至图8可得蜗杆砂轮磨齿机磨削过程中对Δx、Δy、Δz、Δα、Δβ、Δγ影响较大的关键几何误差项，如表4所示。

图5 YW7232 型蜗杆砂轮磨齿机几何误差对Z 方向位置误差分量的敏感度系数Fig. 5 Sensitivity coefficient of geometric errors to Z-direction position error component of YW7232 worm wheel gear grinding machine

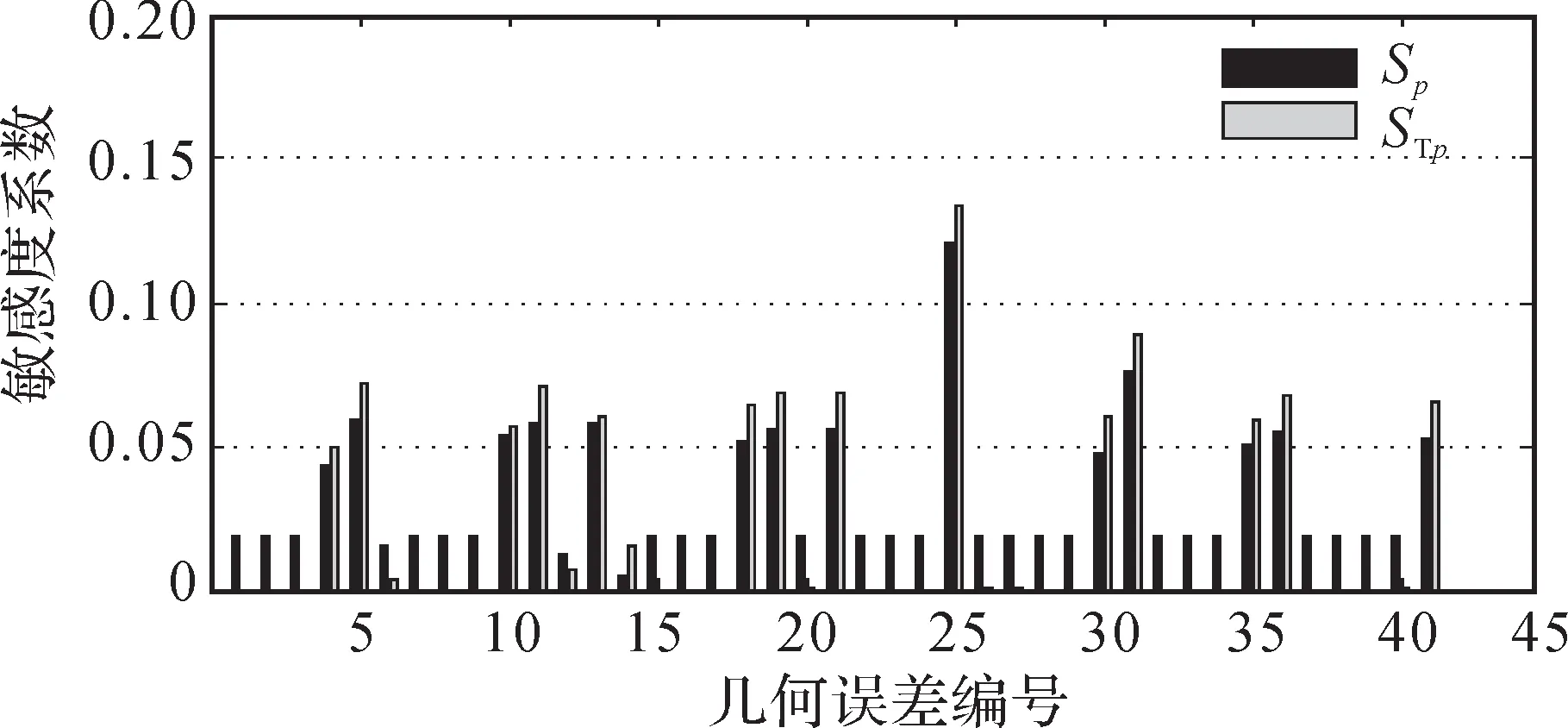
图6 YW7232型蜗杆砂轮磨齿机几何误差对X 方向角度误差分量的敏感度系数Fig. 6 Sensitivity coefficient of geometric errors to X-direction angular error component of YW7232 worm wheel gear grinding machine

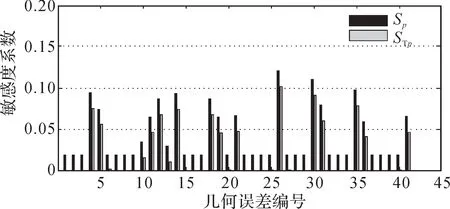
图7 YW7232 型蜗杆砂轮磨齿机几何误差对Y 方向角度误差分量的敏感度系数Fig. 7 Sensitivity coefficient of geometric errors to Y-direction angular error component of YW7232 worm wheel gear grinding machine

图8 YW7232 型蜗杆砂轮磨齿机几何误差对Z 方向角度误差分量的敏感度系数Fig. 8 Sensitivity coefficient of geometric errors to Z-direction angular error component of YW7232 worm wheel gear grinding machine

表4 YW7232型蜗杆砂轮磨齿机的关键几何误差项Table 4 Key geometric error terms of YW7232 worm wheel gear grinding machine

2）由表4可知，对蜗杆砂轮磨齿机空间误差分量影响较大的几何误差为εx(x)、εy(x)、εz(x)、εx(y)、εy(y)、εz(y)、εx(z)、εy(z)、φxz、φzy、φxy、εx(a)、εy(a)、εz(a)、φza、φya、εx(c)、εy(c)、φxc、φyc，共20项。

3）由图3至图8可知，几何误差对Δx、Δy、Δz的全局敏感度系数和一阶敏感度系数大致相同，而对Δα、Δβ、Δγ的全局敏感度系数和一阶敏感度系数有差别，说明几何误差之间的耦合作用对位置误差分量的影响比对角度误差分量的影响小。

4）对空间误差分量影响较大的是角度误差，而定位误差和直线度误差对空间误差分量的影响较小，与角度误差相比可以忽略不计，但角度误差比定位误差和直线度误差更难补偿，因此，在机床设计和制造阶段识别关键几何误差是很有必要的，可以从根本上提高机床的精度。

4 蜗杆砂轮磨齿机几何误差敏感度分析结果验证与讨论

为了验证蜗杆砂轮磨齿机几何误差敏感度分析结果的正确性，对机床关键几何误差进行修正，并对比修正前后机床空间误差分量以及机床联动运动轨迹。首先，对比关键几何误差修正前后机床空间误差分量，把影响某一空间误差分量的关键几何误差项修正为0，其他误差项保持不变，对比修正前后X、Y、Z三个方向的位置误差分量和角度误差分量，修正后空间误差分量越小，表明修正的几何误差对空间误差分量的影响越大。

以y = 20 mm为例，计算在t =1-20 s时关键几何误差修正前后蜗杆砂轮磨齿机的空间误差分量，结果如图9至图14所示。

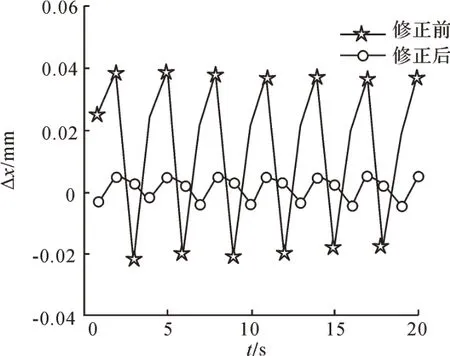
图9 关键几何误差修正前后蜗杆砂轮磨齿机X方向位置误差分量Fig. 9 X-direction position error component of worm wheel gear grinding machine before and after key geometric error correction

图10 关键几何误差修正前后蜗杆砂轮磨齿机Y 方向位置误差分量Fig. 10 Y-direction position error component of worm wheel gear grinding machine before and after key geometric error correction

由图9 至图14 可知，对影响蜗杆砂轮磨齿机空间误差分量的关键几何误差项进行修正后，蜗杆砂轮磨齿机X、Y、Z方向的位置误差分量和角度误差分量都明显减小，且接近于0，说明修正的几何误差项对蜗杆砂轮磨齿机空间误差分量的影响很大，证明了敏感度分析结果的正确性。

其次，对比关键几何误差修正前后机床联动运动轨迹。对20项关键几何误差进行修正后，在机床常用的加工区间内通过仿真模拟球杆仪的3种测量模式：X-Y-C 联动测量模式、X-Z 联动测量模式和Y-Z联动测量模式，并对比修正前后的球杆仪的杆长。3种测量模式示意图及关键几何误差修正前后球杆仪的杆长对比如图15 至图17 所示。图中标准圆的半径为球杆仪的标准长度，记为100 mm，图中一个刻度代表0.01 mm。

图11 关键几何误差修正前后蜗杆砂轮磨齿机Z 方向位置误差分量Fig. 11 Z-direction position error component of worm wheel gear grinding machine before and after key geometric error correction

图12 关键几何误差修正前后蜗杆砂轮磨齿机X 方向角度误差分量Fig. 12 X-direction angular error component of worm wheel gear grinding machine before and after key geometric error correction

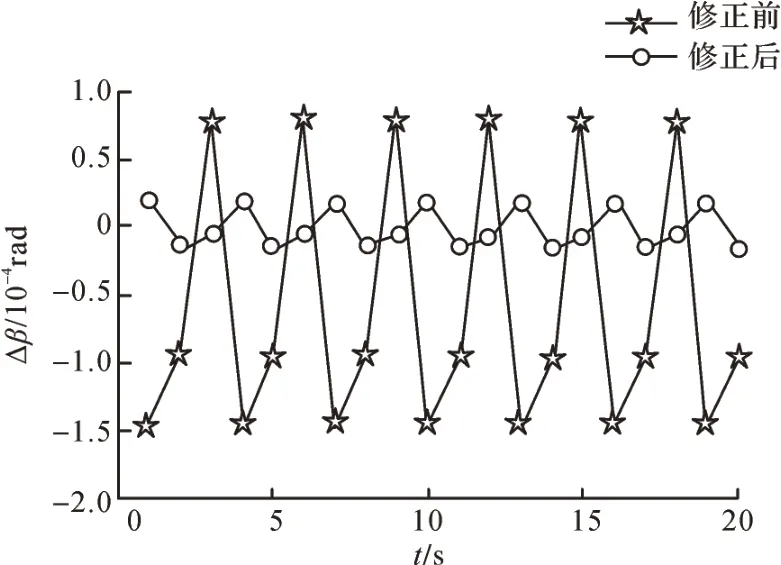
图13 关键几何误差修正前后蜗杆砂轮磨齿机Y 方向角度误差分量Fig. 13 Y-direction angular error component of worm wheel gear grinding machine before and after key geometric error correction

由图15至图17可知，对关键几何误差进行修正后，蜗杆砂轮磨齿机的联动精度明显改善，这说明通过敏感度分析结果对机床进行精度设计和误差补偿，可以高效快速地提高机床空间精度。

图14 关键几何误差修正前后蜗杆砂轮磨齿机Z 方向角度误差分量Fig. 14 Z-direction angular error component of worm wheel gear grinding machine before and after key geometric error correction

图15 X-Y-C联动测量模式及该模式下球杆仪的杆长Fig. 15 X-Y-C linkage measurement mode and rod length of ballbar in this mode

5 结 论

本文针对蜗杆砂轮磨齿机结构复杂、几何误差种类多引起的建模困难、几何误差测量及补偿复杂的问题，提出了一种基于旋量理论和Sobol法的蜗杆砂轮磨齿机几何误差敏感度分析方法。

(b) X-Z联动测量模式下的杆长图16 X-Z联动测量模式及该模式下球杆仪的杆长Fig. 16 X-Z linkage measurement mode and rod length of ballbar in this mode

图17 Y-Z联动测量模式及该模式下球杆仪的杆长Fig. 17 Y-Z linkage measurement mode and rod length ofballbar in this mode

1）基于旋量理论，建立了蜗杆砂轮磨齿机几何误差模型。

2）基于Sobol法，计算了蜗杆砂轮磨齿机磨削过程中各几何误差对空间误差分量的敏感度系数，识别出影响机床空间误差分量的关键几何误差项。

3）通过仿真分析，对比了关键几何误差修正前后蜗杆砂轮磨齿机的空间误差分量和3种测量模式下球杆仪的杆长，验证了敏感度分析结果的有效性。

4）根据敏感度分析结果，对机床进行误差测量和补偿，可高效快速地提高机床空间精度；将敏感度分析结果用于指导机床设计与装配，可从根源上改善机床空间精度。