单级柔顺正交位移放大机构非线性建模与优化

孔垂旺，陈为林，卢清华，罗陆锋，张云志

（佛山科学技术学院机电工程学院，广东佛山528000）

在微血管外科手术、细胞操作、光纤装配、柔性导线理线焊接等精密工程应用中［1-4］，均需利用微夹钳实现微纳尺度物体的夹取、搬运与放置。一方面，柔顺机构具有无间隙、无摩擦、免装配等优点，是微纳操作系统末端执行器的典型实现形式［5］；另一方面，压电驱动器响应速度快，分辨率高［6］，是微夹钳的常用驱动方式之一。对基于柔顺机构的压电驱动微夹钳而言，同时实现操作的灵活性和稳定性是国内外研究者普遍关注的热点［7-8］。

提高输出端行程可有效扩大压电驱动柔顺微夹钳的夹取范围，实现灵活操作。由于典型的压电叠堆驱动器的输出行程仅约为其自身长度的0.1%［9］，为提高微夹钳输出端行程，需将驱动器与位移放大机构匹配使用。常用的柔顺位移放大机构包括杠杆放大机构、柔顺正交位移放大机构、Scott-Russell 机构等［10-13］。其中，以桥式放大机构、单力输入单级柔顺正交位移放大机构为代表的柔顺正交位移放大机构可以通过压电叠堆驱动器的直线位移输出转换来实现平行夹持，提高微纳操作的稳定性。桥式放大机构结构紧凑且理论位移放大倍数大，有关该机构静力学建模、动力学建模、结构优化等的研究较多［14-22］，但它仅在双向对称输入力作用下才能实现正交位移转换。对于微纳操作系统中的压电叠堆驱动器，一端固定一端输出的边界条件更有利于其预紧的便捷性与稳定性，但这种边界条件无法与桥式放大机构相匹配。而单力输入单级柔顺正交位移放大机构可以在单向力输入下兼顾紧凑性的同时实现正交位移转换和位移放大。Chen等［23］提出了抑制单力输入单级柔顺正交位移放大机构几何非线性作用的约束条件。刘敏等［24］提出了单力输入单级柔顺正交位移放大机构的拓扑优化设计方法，并深入研究了弹簧刚度对拓扑优化结果的影响规律。

在上述研究中，对柔顺正交位移放大机构的建模普遍基于2 个假设：1）机构中的柔性单元满足欧拉-伯努利梁假设，且剪切作用可以忽略；2）柔性单元服从小变形假定。然而，当柔性单元长径比不够大时，剪切作用会引起梁的附加挠度，对机构输出位移产生非线性影响。而且在柔顺正交位移放大机构中，柔性单元处于输入力主导的弯曲变形状态，大变形、应力刚化问题不可忽略。常用的几何非线性分析方法包括椭圆积分法、有限单元法、链式算法、梁约束模型法和半解析非线性建模法等［25-29］，其中：椭圆积分法适用于简单柔性单元的几何非线性解析建模；有限单元法、链式算法可用于精确描述复杂柔顺机构的几何非线性行为，但无法获得解析解，且求解时间长；梁约束模型法可用于描述中等变形柔性单元的几何非线性行为，但在大变形条件下模型的精度不足；半解析非线性建模法是将线弹性建模、几何非线性有限元分析与数值拟合相结合，可实现非线性结果的快速、精确预测。

本文拟对单力输入单级柔顺正交位移放大机构进行非线性建模与优化设计。首先，考虑到剪切作用与几何非线性因素，对单级柔顺正交位移放大机构输出位移进行半解析建模，以实现非线性结果的快速预测；然后，综合考虑2种几何非线性因素的影响，对该机构平面尺寸和厚度进行优化设计；最后，利用有限元仿真对机构输出位移非线性模型和优化结果的有效性进行验证。

1 机构输入输出关系非线性建模

1.1 考虑剪切作用的小变形建模

单力输入单级柔顺正交位移放大机构是一种基于三角放大原理的非完全对称型机构［12］，如图1 所示。该机构厚度均匀，仅关于输入力Fin对称，通过引入含3个待定参数（Ld、Bd、γ）的等截面梁CD实现正交位移转换，梁CD的设计方程参见文献［12］。等截面梁CD的下端与机架固联，使得机构避免采用双向对称输入力。变截面梁AB由柔顺铰链a、b和等截面梁2 组成，lBC1、lCC1表示其输出端结构的平面尺寸。其中，柔顺铰链a、b的结构型式不限，图1（a）中采用的是典型的直梁型柔顺铰链。

图1 单力输入单级柔顺正交位移放大机构和三角放大原理示意图Fig. 1 Diagram of single-stage compliant orthogonal displacement amplification mechanism with single-force input and triangulation amplification principle

变截面梁AB 的受力分析如图2 所示，载荷FxB、FyB、MB均作用于B点。变截面梁的位移边界条件为：yA=0 μm，θA=0°，xB=0 μm，θB=0°，其中θA与θB表示点A、B处的转角。

在小变形假定下，采用柔度矩阵法对变截面梁

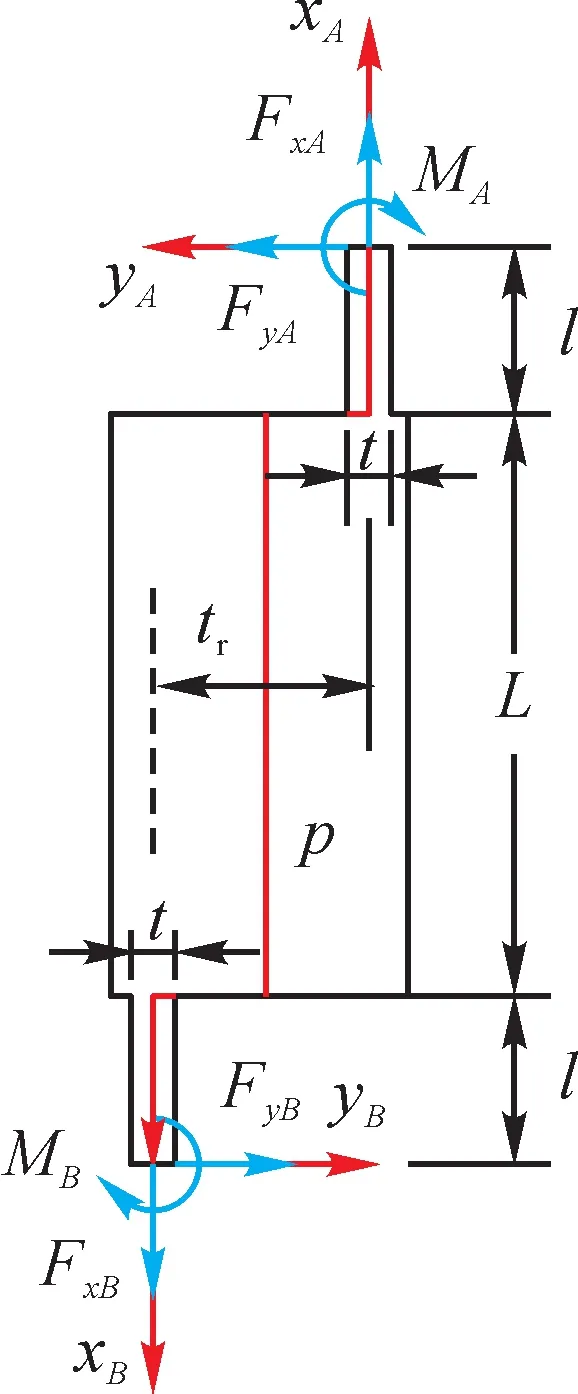
图2 变截面梁AB的受力分析Fig. 2 Force analysis of variable section beam AB

AB中点A、B处的载荷位移关系进行分析，可得：

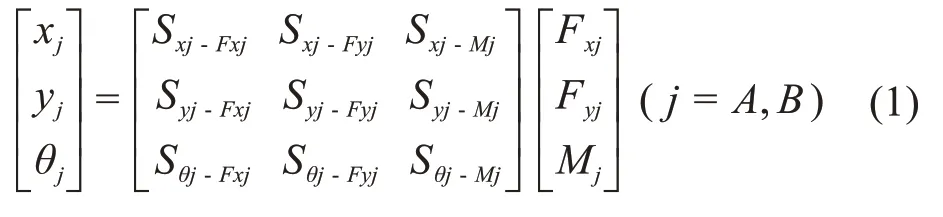
根据式（1）可得yB与B点载荷间的关系为：

式中：SyB-FxB、SyB-FyB、SyB-MB为变截面梁AB的柔度系数。

依据卡式第二定理得：

假设变截面梁AB为欧拉-伯努利梁，则可忽略剪切作用，其应变能UAB由轴向分量和弯曲分量组成：

式中：LAB、AAB、IAB分别为变截面梁AB的长度、横截面积和横截面惯性矩；E为材料弹性模量；FAB为变截面梁AB轴力，与载荷FyB无关；MAB为变截面梁AB的弯矩，是关于载荷FxB、FyB、MB的函数。

联立式（3）和式（4）可推导出SyB-FxB、SyB-FyB、SyB-MB的具体表达式。

图1（b）所示结构呈一次超静定，输入端结构AO由结构AB-BC-CD 和移动副支承。由于移动副转动刚度远大于结构AB-BC-CD的转动刚度，若输入端结构具有足够大的刚度，则MA趋于0，结合式（1），可将A点处的转角—载荷关系简化为：θA=SθA-FxA· FxA+SθA-FyA·FyA。结合θA=0°和变截面梁AB 的载荷平衡方程，可得FxB与FyB间的关系为：

依据变截面梁AB 在结构和载荷方向上的反对称特征可得点A、B处的柔度系数间的关系为：SθA-FxA=SθB-FxB，SθA-FyA=SθB-FyB。根据边界条件θB=0°以及式（1）

可得：

yB的绝对值即为单力输入单级柔顺正交位移放大机构的输出位移eout，故可将式（7）视为在小变形假定下不考虑剪切作用与几何非线性因素的单力输入单级柔顺正交位移放大机构的输出位移模型。用kc表示式（7）中Fin的系数，将式（7）中yB记为yBsE，考虑剪切作用对输出位移yBsE的影响，进一步构造yBsE的修正系数α：

式中：yBs表示机构输出位移的小变形分析值，可通过ANSYS Workbench小变形静力学有限元分析获得。

剪切作用引起的非线性项与机构中柔顺铰链的平面尺寸l、t，厚度h以及表征柔顺铰链间距的参数L、tr有关，即α为关于l、t、h、L、tr的函数。随着柔顺铰链长径比l/t的增大，由剪切作用引起的非线性项逐渐减小［30］，使得剪切非线性修正系数α减小。对于任意材料与输入力Fin，在不同L/tr下α随柔顺铰链长径比l/t（通过固定l、改变t获取不同长径比）的变化曲线如图3所示。

图3 不同L/tr下α随长径比l/t 的变化曲线Fig. 3 Variation curves of α over aspect ratio l/t under different L/tr

由图3可知：在不同L/tr下，随着h的增大，α均逐渐减小；随着L/tr的增大，α逐渐增大。此外，图3是通过固定l、改变t获取不同的l/t，通过固定tr、改变L 获取不同的L/tr的。如果通过固定t、改变l获取不同的l/t，或者通过固定L、改变tr获取不同的L/tr，所得到的α的变化曲线会与图3略有区别，由此可见：除了长径比l/t外，t或l均会对α产生独立影响；除了L/tr外，L或tr均会对α产生独立影响。

基于上述分析，构造无量纲因子φ。在单因素分析中，将与α成反比的l/t、h看作φ的分母，与α成正比的L/tr看作φ的分子，可得：式中：m1、n1、a1、b1、c1为权重系数，m1＞0，n1＞0，a1＞0，

b1＞0，c1＞0。

取m1=4，则n1=2，a1=0.1，b1=2.5，c1=2.1。基于图3所示的180组算例，利用式（9）求取φ，得到180组离散结果，如图4 所示。图4 显示总体上α 随φ 呈单调递增的趋势，利用最小二乘法拟合得：

式中：所有常数仅与机构的拓扑结构以及形状有关，与机构的尺寸、材料无关。

1.2 几何非线性修正系数的确定

几何非线性作用导致yB偏离小变形分析值yBs，为衡量偏离程度，构造yBs的无量纲修正系数β：

式中：变化量Δβ表征机构输出位移的几何非线性程度，变化量Δβ是关于Fin、柔顺铰链尺寸l、t、h以及材料弹性模量E 的函数。随着输入力Fin的增大，单力输入单级柔顺正交位移放大机构输出位移的几何非线性程度提高，即Δβ增大。

取Fin=10 N，选用镁合金（E=45 GPa）、铝合金（E=71 GPa）、钛合金（E=96 GPa）、铜合金（E=110 GPa）和不锈钢（E=193 GPa）五种常见的各项同性材料时，Δβ随柔性铰链长径比l/t的变化曲线如图5所示。

由图5可知，无论选用何种材料，随着l/t的增大，Δβ均逐渐增大；随着h的增大，相同材料下Δβ逐渐减小；随着材料弹性模量E 的增大，Δβ 逐渐减小。此外，图5是通过固定l、改变t获取不同l/t值的，如果通过固定t、改变l获取不同的l/t值，所得到的Δβ变化曲线与图5 略有区别，由此可见除了长径比l/t外，t或l也会分别对Δβ产生独立影响。

图4 α随φ的变化曲线及其最小二乘拟合结果Fig. 4 Variation curves of α over φ and its least squares fitting result

图5 选用不同材料时Δβ随长径比l/t的变化曲线（Fin=10 N）Fig. 5 Variation curves of Δβ over aspect ratio l/t when using different materials（Fin=10 N）

基于上述分析，构造无量纲因子ω。在单因素分析中，将与Δβ成正比的Fin、l/t看作ω的分子，与Δβ成反比的E、h看作ω的分母，可得：

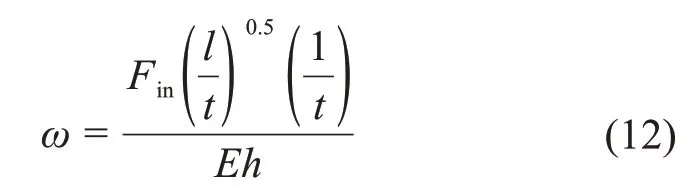
根据图5所示的180组算例，分别取Fin=1，2，…，10 N，利用式（12）求取ω，得到1 800 组离散结果，如图6所示。由图6可见总体上Δβ随ω单调递增，利用最小二乘法拟合得：

式中：所有常数仅与机构的拓扑结构和形状有关，与机构的尺寸、材料无关。

图6 Δβ随ω的变化曲线及其最小二乘拟合结果Fig. 6 Variation curves of Δβ over ω and its least squares fitting result

2 机构参数的非线性优化设计

一方面，为了增大单力输入单级柔顺正交位移放大机构的工作空间，选择eout=|yB|最大化作为优化目标。综合式（7）、式（8）、式（11）可得：

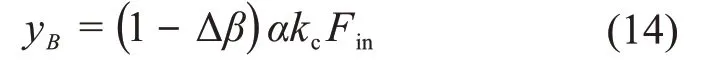
另一方面，若Δβ很小（例如Δβ≤0.02），则单力输入单级柔顺正交位移放大机构的几何非线性作用几乎被完全抑制。此时，eout=|yB|最大化可以简化为αkc最大化，以减弱输入输出关系的非线性特征，便于后续研究。

依据第1节所述的单力输入单级柔顺正交位移放大机构输入输出关系非线性建模过程，选取设计变量为l、t、L、tr、h。柔顺铰链的抗弯刚度EIa应远大于等截面梁2 的抗弯刚度EI2，以保证机构柔度集中于柔顺铰链处；在线弹性解析建模过程中，将柔顺铰链a、b和等截面梁2看作一个整体，限制l/t和L/b2的下限（b2为等截面梁宽度）及tr的上限；考虑到紧凑性和加工能力，应限制l/t的上限以及l、t、h、tr的下限；考虑到柔性铰链是在平面内转动，应限制铰链宽度t与厚度h。综上分析，建立2种单力输入单级柔顺正交位移放大机构参数优化模型：

1）优化模型1：

2）优化模型2：

min: - αkcs.t.

取初始设计参数为：lmin=1 mm，lmax=3 mm，tmin=0.3 mm，Lmax=12 mm，trmin=1 mm，trmax=2 mm，hmin=1.2 mm，铰链最大长径比rmax=8；输出端结构参数lBC1=1.1 mm，lCC1=0.5 mm，材料设置为铝合金，输入力Fin=10 N。基于优化模型1，利用MATLAB fmincon 梯度优化函数对单力输入单级柔顺正交位移放大机构的参数进行优化，结果如表1所示。当采用不同初始值进行测试时，结果均稳定收敛于表1中的优化结果，且优化结果与材料和输入力Fin无关。利用前期研究［12］中的设计方程计算出与表1优化结果对应的等截面梁CD的待定结构参数，如表2所示。

表1 基于优化模型1的单力输入单级柔顺正交位移放大机构参数优化结果Table 1 Parameter optimization results of single-stage compliant orthogonal displacement amplification mechanism with single-force input based on optimization model 1 单位：mm

表2 基于优化模型1的等截面梁CD的待定结构参数Table 2 Pending structural parameters of constant-section beam CD based on optimization model 1

在不改变初始设计参数的前提下，基于优化模型2，利用MATLAB fmincon梯度优化函数对采用不同材料的单力输入单级柔顺正交位移放大机构的参数进行优化，结果如表3所示。当采用不同初始值进行测试时，结果均稳定收敛于表3中的优化结果，且随着材料弹性模量E增大，柔性铰链的厚度h逐渐减小。与表3优化结果对应的等截面梁CD的待定结构参数均为：Ld=7 mm，Bd=0.25 mm，γ=0.76°。

表3 基于优化模型2的单力输入单级柔顺正交位移放大机构参数优化结果Table 3 Parameter optimization results of single-stage compliant orthogonal displacement amplification mechanism with single-force input based on optimization model 2 单位：mm

3 机构输出位移非线性模型和优化结果的有限元仿真验证

本节通过小变形静力学有限元仿真验证剪切非线性修正系数α拟合结果的准确性，并结合几何非线性静力学有限元仿真验证几何非线性修正系数β拟合结果的准确性，最后通过有限元仿真验证优化结果的有效性。

对材料与结构参数均不同的单力输入单级柔顺正交位移放大机构进行静力学有限元仿真分析，取5组算例，各算例中变截面梁AB 的参数设置如表4所示。对于表4中的5组算例，变截面梁AB输出端结构参数lBC1=1.1 mm，lCC1=0.2 mm，计算得到各算例中等截面梁CD 的待定结构参数，如表5 所示。在5 组算例中，柔性铰链的长径比l/t值分别为5.50，4.00，5.00，4.29，8.00，其中，算例I、Ⅳ中变截面梁AB 不满足欧拉-伯努利梁假设。

表4 各算例中变截面梁AB的参数设置Table 4 Parameter setting of variable section beam AB in each example 单位：mm

表5 各算例中等截面梁CD的待定结构参数Table 5 Pending structural parameters of constant-section beam CD in each example

3.1 考虑剪切作用的小变形建模验证

利用ANSYS Workbench小变形静力学有限元仿真分别获取各组算例的yBs值，其中输入力Fin=10 N。算例I对应的单力输入单级柔顺正交位移放大机构的小变形静力学有限元仿真结果如图7与图8所示。图7中X正方向与图2中yB正方向相同。通过对比5组算例的yBs的理论值和仿真值可知，两者的相对误差分别为0.01%，5.38%，1.72%，3.42%，3.38%，均小于6.00%，说明剪切非线性修正系数α 的拟合结果准确。

图7 算例I 对应的单力输入单级柔顺正交位移放大机构的边界条件设置与小变形静力学有限元仿真结果(Fin=10 N)Fig. 7 Boundary condition setting and small deformationbased static finite element simulation results of singlestage compliant orthogonal displacement amplification mechanism with single-force input corresponding to example I(Fin=10 N)

3.2 几何非线性修正系数模型验证

对于表4 中的5 组算例，分别取Fin=1，2，…，10 N，在不同输入力下通过几何非线性静力学有限元仿真（边界条件如图7（a）所示）和小变形静力学有限元仿真分别求出yB值和yBs值，结果如图9所示，进而计算β的仿真值，并与基于式（12）和式（13）求出的理论值进行对比，结果如图10所示。通过对比可知5组算例β 的理论值和仿真值的相对误差分别为1.61%，0.89%，2.10%，1.50%，1.51%，均小于2.50%，说明几何非线性修正系数β的拟合结果准确。

图8 yBs的理论值与小变形静力学有限元仿真值对比Fig. 8 Comparison of theoretical values and small deflection-based static finite element simulation values of yBs

图9 算例I 对应的单力输入单级柔顺正交位移放大机构的几何非线性静力学有限元仿真结果(Fin=10 N)Fig. 9 Geometrical nonlinear static finite element simulation results of single-stage compliant orthogonal displacement amplification mechanism with single-force input corresponding to example I(Fin=10 N)

3.3 非线性优化结果验证

表4 中算例I、II、V对应的单力输入单级柔顺正交位移放大机构的参数满足优化模型1的约束条件，可将它们设为初始组，表6为初始组与基于优化模型1 优化的yB的有限元仿真值对比。依据基于优化模型1的优化结果，可构造3组具有最大理论位移放大倍数的对照组，分别与算例I、II、V对应，各对照组中变截面梁AB 的尺寸参数为：l=2.40 mm，t=0.30 mm，L=12 mm，tr=1 mm，h=1.2 mm。取输出端结构参数lBC1=1.1 mm，lCC1=0.2 mm，计算得到相应的梁CD 的待定结构参数：Ld=10.75 mm，Bd=0.31 mm，γ=1.98°。相对于初始组，优化组输出位移的几何非线性程度提高，但输出位移显著增大。尽管对照组具有最大理论位移放大倍数，但优化组具有更大的输出位移，说明优化结果有效。

表6 初始组、优化组与对照组的yB、β 的有限元仿真值对比（Fin=10 N）Table 6 Comparison of finite element simulation values of yB and β in the initial group, optimal group and control group (Fin=10 N)

基于优化模型2优化的yB和β的有限元仿真值如表7 所示。在优化组II（镁合金）中，β 控制在约束范围内；在其它优化组中，尽管β超出约束范围，但β的有限元仿真值相对于约束条件中β的阈值的误差分别为0.07%，0.05%，0.07%，0.11%，0.20%，均小于0.50%，说明优化结果有效。

图10 β的理论值与有限元仿真值对比Fig. 10 Comparison of theoretical values and finite element simulation values of β

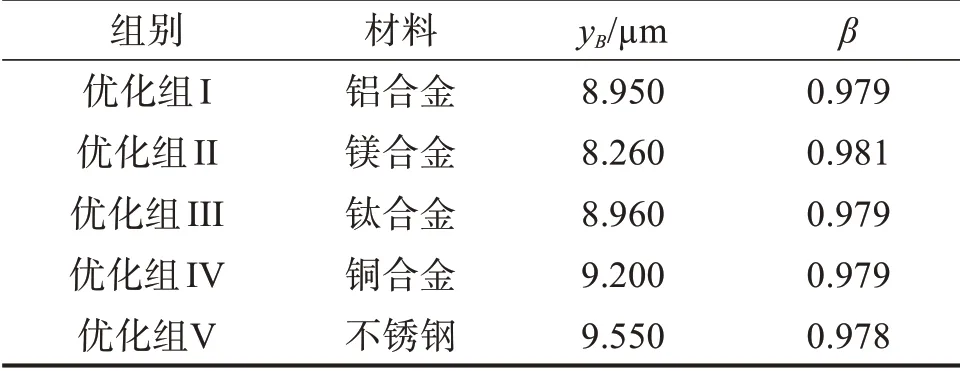
表7 基于优化模型2的yB、β的有限元仿真值（Fin=10 N）Table 7 Finite element simulation values of yB and β based on optimization model 2（Fin=10 N）

4 结 论

本文对单力输入单级柔顺正交位移放大机构进行了非线性建模与参数优化。通过对机构输入输出关系的两步法半解析建模，实现了非线性结果的快速预测。结合卡式第二定理、有限元仿真法与最小二乘拟合法，建立了剪切非线性修正系数与无量纲尺寸参数因子间的二阶多项式模型。基于有限元仿真法与最小二乘拟合法，建立了几何非线性修正系数与无量纲结构尺寸、载荷参数的三阶多项式拟合模型。通过ANSYS Workbench有限元仿真验证了上述2个模型的准确性，其误差均小于5%。综合考虑输出位移最大化与抑制几何非线性的影响，提出2种平面尺寸和厚度综合优化策略，并利用ANSYS Workbench有限元仿真验证了优化结果的有效性。利用本文方法对单级柔顺正交位移放大机构进行非线性建模与优化，可有效提高压电驱动柔顺微夹钳的位移输出性能与开环控制的精度和实时性，有利于实现稳定灵活的微操作。