改进人工蜂群算法优化的LSSVM在混合气体定量分析中的应用

李成兵，叶 超，毛熙皓

（西南石油大学机电工程学院，四川成都610500）

易燃易爆气体泄漏引发的燃烧和爆炸事故在石油化工、交通运输等行业时有发生。常见的易燃易爆气体有酒精气体、甲烷、一氧化碳和氢气等，一般情况下，泄漏的易燃易爆气体并非单一性质气体，而是几种气体的混合体。因此，对易燃易爆混合气体进行定量分析具有非常重要的意义，但因各气体传感器间存在交叉敏感性［1］，不能实现对各组分气体浓度的精确测量。目前，提高混合气体中各组分气体浓度测量精度的方法主要有支持向量机（support vector machine，SVM）［2-3］、最小二乘支持向量机［4-7］和BP（back propagation，反向传播）神经网络［8-11］等。金翠云等人［2］利用PSO 算法对SVM 的参数进行了优化，并将优化后的SVM应用于气体定量分析，减小了测量误差。曲健等人［3］利用自适应PSO算法优化了SVM的参数，并与利用遗传算法优化的结果进行对比，发现采用自适应PSO 算法时分析模型的建模时间较长，但预测精度较高。曾燕等人［4］将LSSVM应用于下水道可燃气体的定量分析。李玉军等人［5］将PSO 算法与LSSVM 相结合，建立了混合气体定量分析模型，提高了混合气体中各组分气体浓度的测量精度。丁续达等人［6］利用LSSVM对燃煤发电排放的NOx的浓度进行了在线预测。丁知平等人［7］使用引力算法优化了LSSVM，从而提高了NOx浓度的预测精度。王春晨等人［8］将BP神经网络与PID（proportion integration differentiation，比例积分微分）控制器相结合，实现混合气体的配比。张瑞华［9］通过BP人工神经网络建立了一定浓度可燃混合气体的爆炸超压模型。黄伟军等人［10］改进了BP神经网络，实现了汽车尾气各组分气体浓度的测量。龚雪飞等人［11］利用PSO算法对BP神经网络进行优化，实现了多元有害气体的浓度测量，并提高了测量精度。BP神经网络的收敛精度和预测精度与其网络结构的选择有很大关系，因此其输出具有不可预测性和不一致性，且BP神经网络的本质为梯度下降法，其学习的时间较长，而LSSVM可以很好地避开上述问题。

为此，笔者提出一种利用改进人工蜂群算法优化LSSVM的方法，对含有酒精气体、甲烷、一氧化碳和氢气的混合气体进行定量分析。首先，通过在标准人工蜂群算法中引入自适应递减因子以更新搜索步长，并结合轮盘赌与反向轮盘赌机制来改进待工蜂跟随概率公式，以提高搜索精度；然后，利用IABC算法对LSSVM 的惩罚参数C 和核参数σ2进行优化，使LSSVM拥有具有更高的计算精度；最后，将优化后的LSSVM用于混合气体定量分析，以提高在交叉敏感状态下混合气体中各组分气体浓度的测量精度。

1 最小二乘支持向量机

最小二乘支持向量机（LSSVM）是由Suykens等［12］在SVM的基础上提出的，将SVM中的不等式约束转变为等式约束，并选取误差平方和作为优化目标函数，使得二次规划问题转化为线性方程组求解问题，从而降低了计算难度。LSSVM在非线性系统建模方面更具有优势［13-14］，其基本思想如下。

给定一个训练数据集T ={( xi，yi)|i=1，2，…，l }，其中输入为n维向量xi，输出为yi，l为训练样本个数，则LSSVM的优化问题可以描述为：

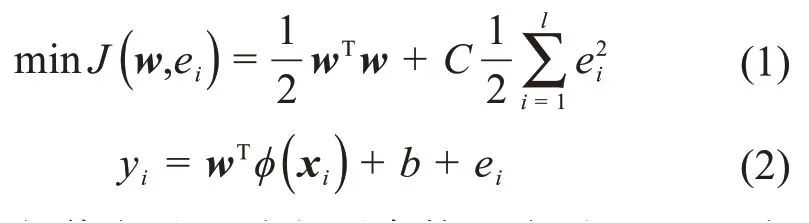
式中：w为权值向量，C为惩罚参数，ei为误差，φ(·)为原空间到高维空间的非线性映射，b为阈值。

由于w可能有无限的维数，直接求解式（1）较为困难，因此引入拉格朗日函数：

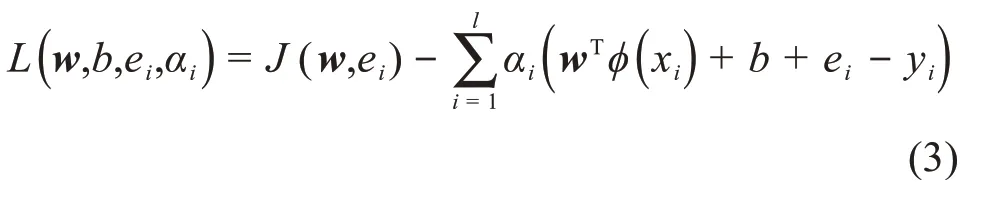
式中：αi≥0，为拉格朗日乘子。

根据取极值的必要条件，设拉格朗日函数对于各个变量的偏导数为零，可得：

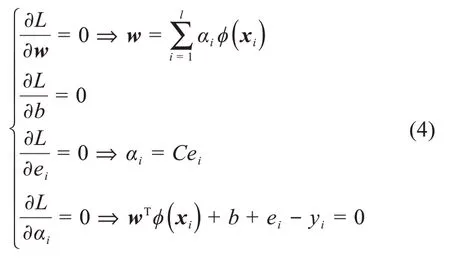
引入核函数：

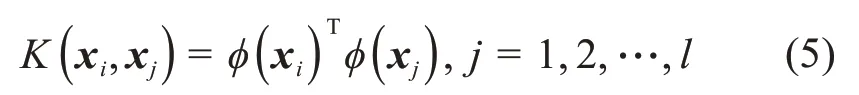
基于核函数，可将式（4）整理为：

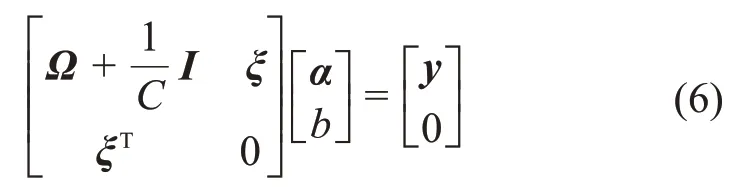
式中：Ω 为一个方阵，其第i 行第j 列元素Ωij=K ( xi，xj)；I为单位矩阵；ξ =[1，…，1]T。

本文选择径向基函数作为核函数：

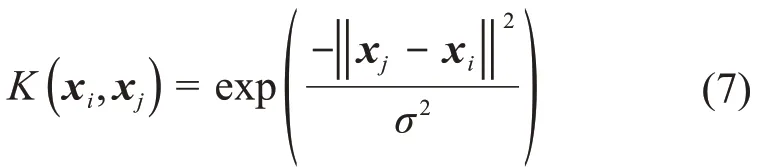
式中：σ2为核宽度。

根据式（6）求出的α 和b 构造用于函数估计的LSSVM模型：

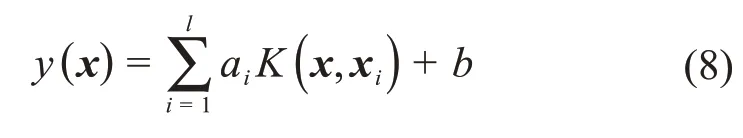
2 人工蜂群算法

2.1 标准人工蜂群算法

标准人工蜂群（ABC）算法于2005年由Karaboga提出［15］，常用于求解函数极值问题。在标准ABC算法中，蜂群由3 种蜂组成：采蜜蜂、待工蜂、侦查蜂。采蜜蜂搜索蜜源，测量蜜源质量即适应度函数值，并将蜜源信息分享给其他蜜蜂；待工蜂通过采蜜蜂分享的信息，以一定的概率选择蜜源进行搜索；侦查蜂随机搜索蜜源。

标准ABC算法实现的具体步骤如下［16-18］：

1）初始化蜜蜂种群。初始时刻所有蜜蜂均为侦查蜂，全局随机搜索蜜源，蜜源的位置代表空间内的可能解向量，蜜源的初始位置在搜索空间随机产生，随机产生的公式为：

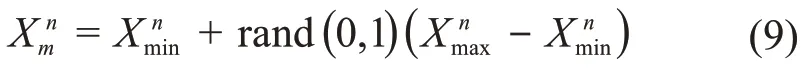
式中：蜜源m（m=1，2，…，N）与蜜蜂一一对应，N为蜜源即蜜蜂个数；Xnm表示蜜源位置，Xnmax和Xnmin分别表示搜索空间的上限和下限，n=1，2，…，D，D 为优化问题参量的个数；rand（0,1）为［0,1］内的随机数。

搜索到蜜源初始位置后，所有侦查蜂转变为采蜜蜂，并测量每个蜜源的适应度函数值（用于衡量蜜源的质量），然后采蜜蜂在蜜源初始位置邻域内搜索新蜜源：

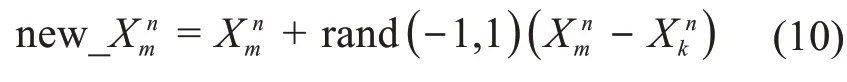
式中：k∈｛1，2，…，N｝，且k≠m；rand（-1，1）为［-1，1］内的随机数。

当新蜜源的适应度函数值优于旧蜜源的适应度函数值时，根据贪婪准则，以新蜜源取代旧蜜源，否则保留旧蜜源。

2）对所有采蜜蜂测量得到的适应度函数值进行排序，排名靠后的采蜜蜂成为待工蜂，一般定义待工蜂和采蜜蜂各占种群一半。然后，采蜜蜂飞回交流区把蜜源信息分享给待工蜂，待工蜂依据轮盘赌机制对蜜源进行选择，选择概率为：

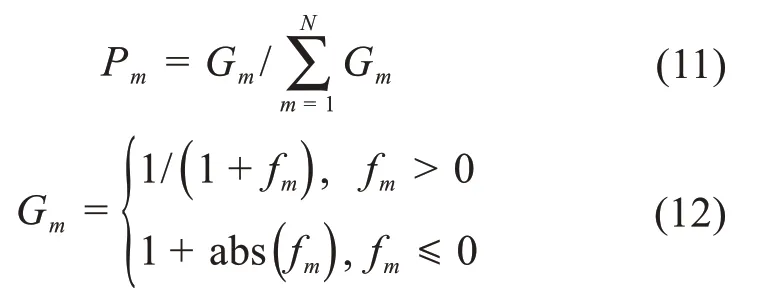
式中：Gm为解的适应度函数值，fm为目标函数值。

对于每只待工蜂，在选择一个蜜源后，按式（10）在该蜜源邻域内寻找其他蜜源，若新蜜源的适应度函数值更优，则取代原蜜源，且该待工蜂转换为采蜜蜂。

对于每只采蜜蜂，在分享信息后，继续在该蜜源附近寻找新蜜源并计算其适应度函数值，然后根据贪婪准则进行选取。

3）若在搜索过程中，经过s次搜索并得到一定的搜索阈值T后仍没有找到更优的蜜源，则采蜜蜂和待工蜂将放弃该蜜源且转变为侦查蜂，并按式（9）重新随机产生一个新的蜜源。

2.2 改进的人工蜂群算法

在标准ABC算法中，蜂群搜索的范围和精度由步长rand（-1，1）决定：当rand（-1，1）较大时，算法收敛速度较快，但随着优化趋近最优值，容易跳过全局最优解；当rand（-1，1）较小时，算法收敛速度较慢，但收敛精度高。对标准ABC算法分析可知，在搜索前期，应取较大的步长，以保证收敛速度，加快向最优解靠拢；在搜索后期，算法搜索到的值逐渐靠近最优解，应逐渐减小步长以实现对最优解周围进行细化搜索，减少在最优值附近的动荡，提高收敛精度。基于此，引入了一种自适应递减因子来更新搜索步长，其公式为：

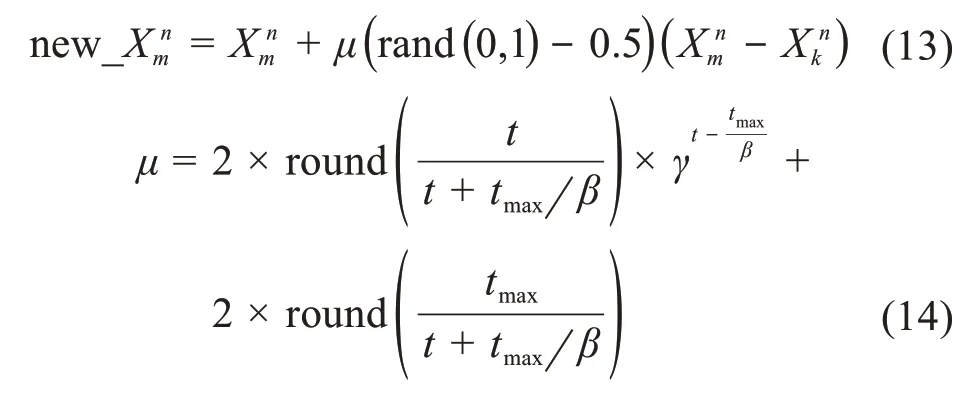
式中：μ为自适应递减因子，round（）为四舍五入函数，t为当前迭代次数，tmax为最大迭代次数，β ∈(1，tmax)且? 不为整数，γ ∈(0，1)。

设tmax=100，当β和γ取不同值时，μ与迭代次数的关系曲线如图1所示。

由图1 可以看出，当γ 相同时，β 值越小，维持大步长的迭代次数越多，说明算法在搜索前期的收敛速度较快；当β相同时，γ值越小，达到最大迭代次数时μ越小，说明算法在搜索后期的收敛精度更高。

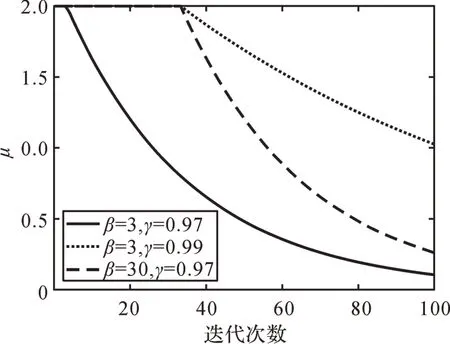
图1 β、γ不同时μ与迭代次数的关系曲线Fig. 1 The relationship between μ and iteration times under different β and γ

同时，在标准ABC算法中，待工蜂按照式（11）对蜜源进行选择，适应度越高的蜜源被选择的概率越大，但这种选择方式会使蜂群在优化过程中朝着适应度高的蜜源集中，而适应度低的蜜源则会被迅速淘汰，这会导致蜂群多样性降低，使得种群早熟收敛而不能达到全局最优。因此，在算法搜索前期应使待工蜂对适应度高的蜜源进行搜索，以保证收敛速度，而在算法搜索后期应使待工蜂对适应度低的蜜源进行适当的跟踪搜索，以保持种群的多样性，避免陷入局部最优。为此，引进反向轮盘赌机制［19］，并结合轮盘赌和反向轮盘赌，改进待工蜂的跟随概率公式，具体改进公式为：

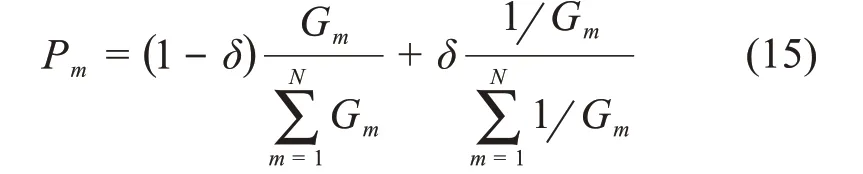
式中

改进后，既保证了算法在搜索前期对高适应度蜜源搜索的收敛速度，又增大了搜索后期稍差适应度蜜源的被选择概率，保持了蜂群的多样性，提高了算法的求泛能力。

3 实验验证

3.1 改进人工蜂群算法性能测试

为测试IABC算法的性能（主要为收敛精度），选取5个常用测试函数进行实验，并与PSO算法进行对比。常用的5个测试函数如表1所示，每个函数的最优值均为0，其中：测试函数Sphere 的搜索范围为［-100，100］，Schaffer 的搜索范围为［-100，100］，Schwefel 的搜索范围为［-500，500］，Griewank 的搜索范围为［-600，600］，Rosenbrock 的搜索范围为［-2.048，2.048］。

表1 常用的5个测试函数Table 1 Five commonly used test functions

设IABC算法的种群规模为20，维数为2，最大迭代次数tmax=100，搜索阈值T=10，γ=0.92，β=1.3。设PSO 算法的种群规模为20，维数为2，最大迭代次数为100，惯性权重因子为0.8，学习因子c1=1.5，c2=1.8。使用MATLAB R2017b进行实验测试，每种优化算法对每个测试函数进行10 次实验，测试结果如表2 所示。通过对比表2中最优值、最劣值和平均值可以看出：IABC 算法对5个测试函数的收敛精度要比PSO算法高，且收敛效果更好。

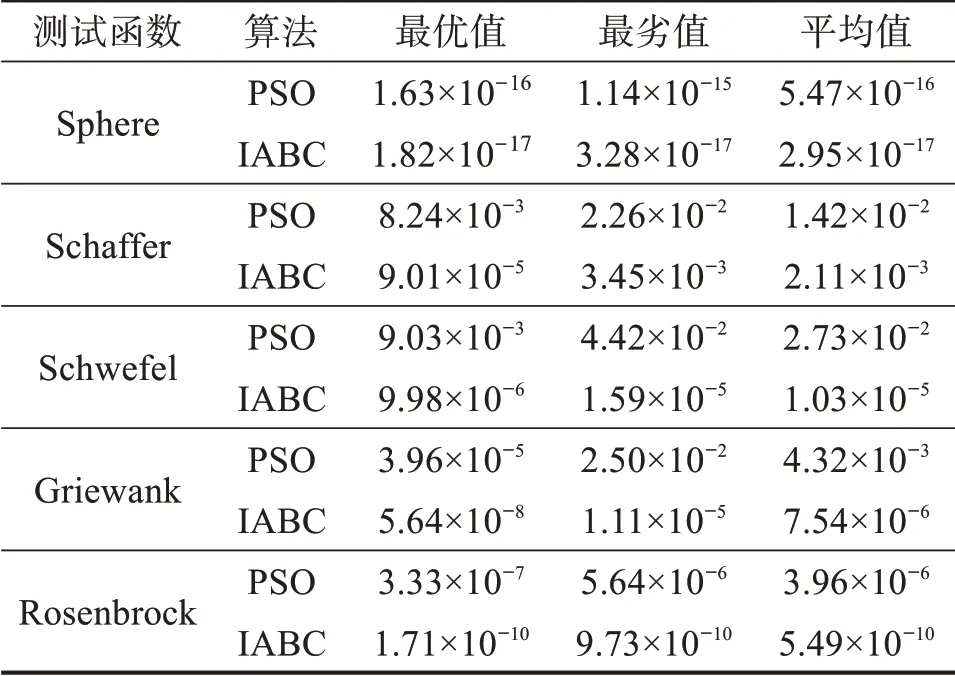
表2 IABC算法和PSO算法的性能测试结果对比Table 2 Comparison of performance test results between IABC algorithm and PSO algorithm

同时，为评价IABC 算法和PSO 算法的复杂度，通过计算各算法的运行时间来对比其复杂度［20］。分别使用IABC 算法和PSO 算法对5 个测试函数进行1 000次迭代，采用高迭代次数是为了使2种算法的优化时间的差异更加显著。每个测试函数进行10次测试，并计算2种算法的平均优化时间，结果如图2所示。由图可知，IABC算法迭代1 000次所用的时间分别为：3.351 s（函数Sphere）、4.447 s（函数Schaffer）、4.361 s（函数Schwefel）、4.099 s（函数Griewank）、4.663 s（函数Rosenbrock），均略低于PSO算法的优化时间（3.459 s（函数Sphere）、4.972 s（函数Schaffer）、4.615 s（函数Schwefel）、4.273 s（函数Griewank）、5.314 s（函数Rosenbrock））。通过对比2种算法的优化时间可知，IABC 算法的迭代速度稍高于PSO 算法，说明计算过程中IABC 算法的复杂度低于PSO算法。

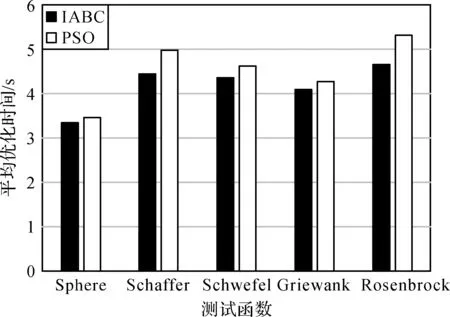
图2 IABC算法和PSO算法优化时间对比Fig. 2 Comparison of optimization time between IABC algorithm and PSO algorithm

3.2 混合气体定量分析实验

在20℃、相对湿度为50%的环境下对包含酒精气体、甲烷、一氧化碳和氢气的混合气体进行浓度检测。酒精气体、甲烷、一氧化碳、氢气四种气体的浓度范围分别为：190～770，260～400，110～470，15～45 mg/m3。实验中使用的传感器为：郑州炜盛电子科技有限公司生产的MQ-3B 酒精传感器，检测浓度范围为47.8～956.7 mg/m3；MQ-4 甲烷传感器，检测浓度范围为199.7～6 655.3 mg/m3；MQ-7B一氧化碳传感器，检测浓度范围为11.6～582.3 mg/m3；MQ-8氢气传感器，检测浓度范围为8.3～83.2 mg/m3。选用的传感器皆为半导体电阻式传感器，各传感器的电导率随着待测气体浓度的增大而增大，拥有较高的灵敏度。采用STM32F103VET6作为单片机最小系统，测试系统原理图和测试环境分别如图3和图4所示。

采集各组分浓度不同的混合气体以及传感器响应值，共计得到50组样本数据，取其中40组样本数据作为训练样本，剩余10组作为测试样本。为使数据更符合算法的输入，需对获取的原始样本进行归一化处理（将样本数据归一化到［0，1］内），归一化公式如下：

图3 混合气体浓度测试系统原理图Fig. 3 Schematic diagram of mixture gas concentration test system

图4 混合气体浓度测试环境Fig. 4 Mixture gas concentration test environment

式中：Uq是采集到的样本数据，Uqmax、Uqmin为数据样本中最大值和最小值。

利用LSSVM 建立混合气体定量分析模型前需对其惩罚参数C和核参数σ2进行合理的优化选择，本文采用IABC算法对惩罚参数和核参数进行寻优，并与常用的混合气体定量分析方法——PSO算法的寻优结果进行对比，具体的寻优过程如下：

1）对LSSVM 的惩罚参数C 和核参数σ2进行初始化，初步建立回归模型。

2）初始化IABC 算法的种群规模、最大迭代次数、搜索阈值、自适应因子等参数以及惩罚参数C和核参数σ2的搜索范围。

3）将模型输出结果的均方误差作为IABC 算法的适应度值，并设定合适的均方误差作为阈值。

4）执行IABC算法，记录并更新最优解。

5）判断优化结果是否满足设定的均方误差或者达到最大迭代次数，若满足则输出最优解，即输出最佳的C和σ2，否则转第4）步。

为提高测量精度，利用LSSVM分别构建酒精气体、甲烷、一氧化碳和氢气的定量分析模型，然后再利用IABC 算法对各组分气体定量分析模型的参数分别进行优化。以甲烷气体定量分析模型的参数优化为例，设IABC算法的种群规模为20，维数为2，最大迭代次数为100，搜索阈值为10，γ=0.92，β=1.3；LSS-VM 惩罚参数C 和核参数σ2的搜索范围设置为（0，100）。根据上述的模型优化流程进行分析，得到基于IABC 算法的甲烷气体定量分析模型参数优化误差曲线，如图5所示。

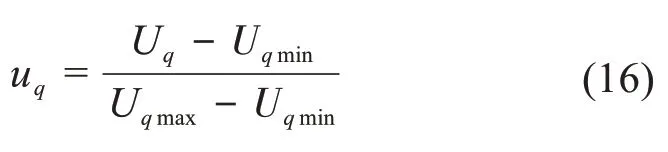
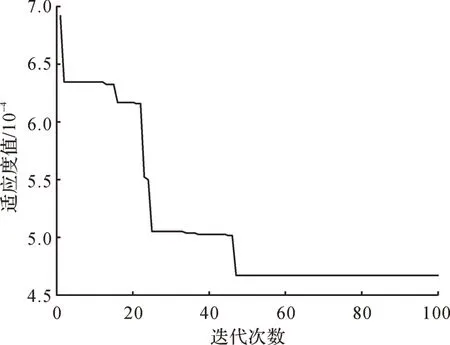
图5 基于IABC 算法的甲烷气体定量分析模型参数优化误差曲线Fig. 5 Optimization error curve of parameters of quantitative analysis model for methane gas based on IABC algorithm

从图5可以看出，IABC算法在经过46次迭代后便找到了最优解，具有较快的收敛速度。IABC算法迭代100 次所用的时间为7.840 s，此时均方误差最小，为4.642×10-4，惩罚参数C=58.260，核参数σ2=9.124。用同样的方法对酒精气体、一氧化碳和氢气的定量分析模型进行优化，得到对应的惩罚参数、核参数、均方误差以及迭代时间，如表3所示。

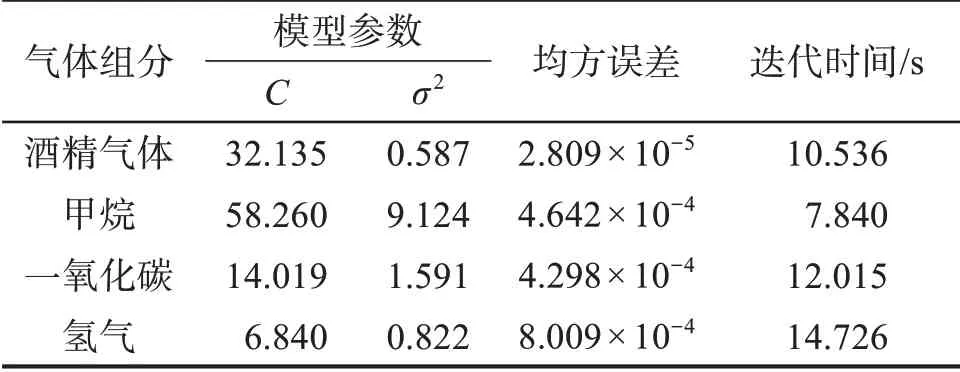
表3 IABC 算法对各组分气体定量分析模型参数的优化结果Table 3 Optimization results of parameters of quantitative analysis model for each component gas by IABC algorithm

同样地，采用PSO 算法对各组分气体定量分析模型进行参数优化。本文设PSO 算法种群规模、维数及最大迭代次数均与IABC 算法相同，分别为20，2，100；PSO 算法惯性权重因子为0.8，学习因子c1=1.5，c2=1.8。PSO 算法的优化流程如图6 所示，基于PSO算法的甲烷气体定量分析模型参数优化误差曲线如图7所示。

由图7 可以看出，PSO 算法在经过51 次迭代后找到了最优解，PSO 算法迭代100 次所用的时间为13.021 s，收敛速度稍慢于IABC 算法。此时均方误差 为3.247×10-3，惩 罚 参 数C=39.331，核 参 数σ2=0.845。用同样的方法对酒精气体、一氧化碳和氢气的定量分析模型进行优化，得到对应的惩罚参数、核参数、均方误差以及迭代时间，如表4所示。

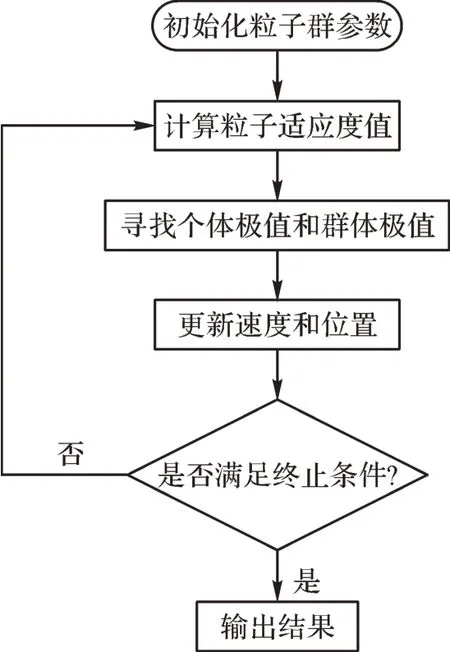
图6 PSO算法优化流程Fig. 6 Optimization process of PSO algorithm

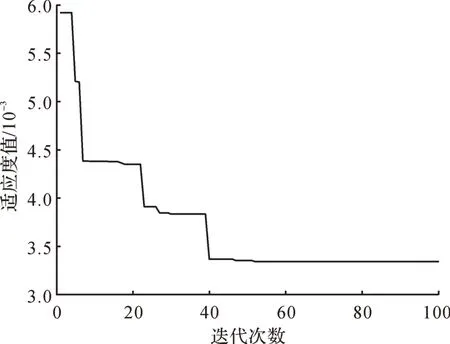
图7 基于PSO 算法的甲烷气体定量分析模型参数优化误差曲线Fig. 7 Optimization error curve of parameters of quantitative analysis model for methane gas based on PSO algorithm

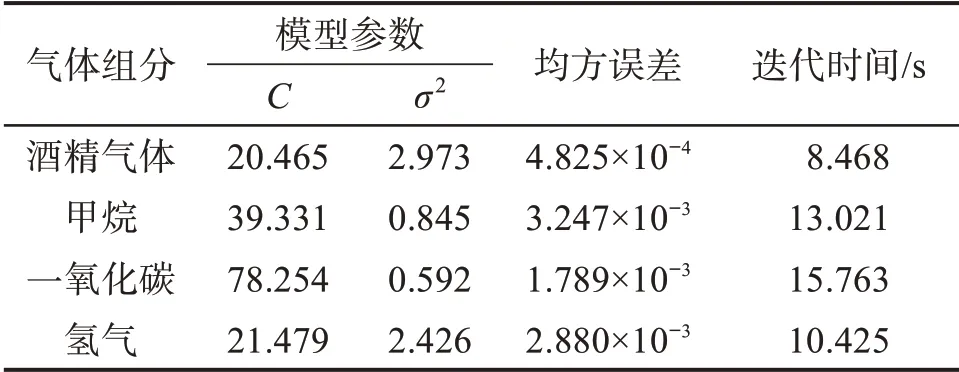
表4 PSO 算法对各组分气体定量分析模型参数的优化结果Table 4 Optimization results of parameters of quantitative analysis model for each component gas by PSO algorithm

结合表3、表4可以看出，IABC算法对各组分气体定量分析模型的优化时间总和为45.117 s，PSO算法对各组分气体定量分析模型的优化时间总和为47.677 s，IABC算法所用的时间略短于PSO算法，且IABC算法对各组分气体定量分析模型参数进行优化后得到的均方误差明显小于PSO算法。将优化得到的惩罚参数和核参数代入LSSVM以重建各组分气体定量分析模型，并对各测试样本的气体浓度进行预测，基于2种算法的混合气体各组分浓度的预测结果如表5所示，预测相对误差分别如图8和图9所示。

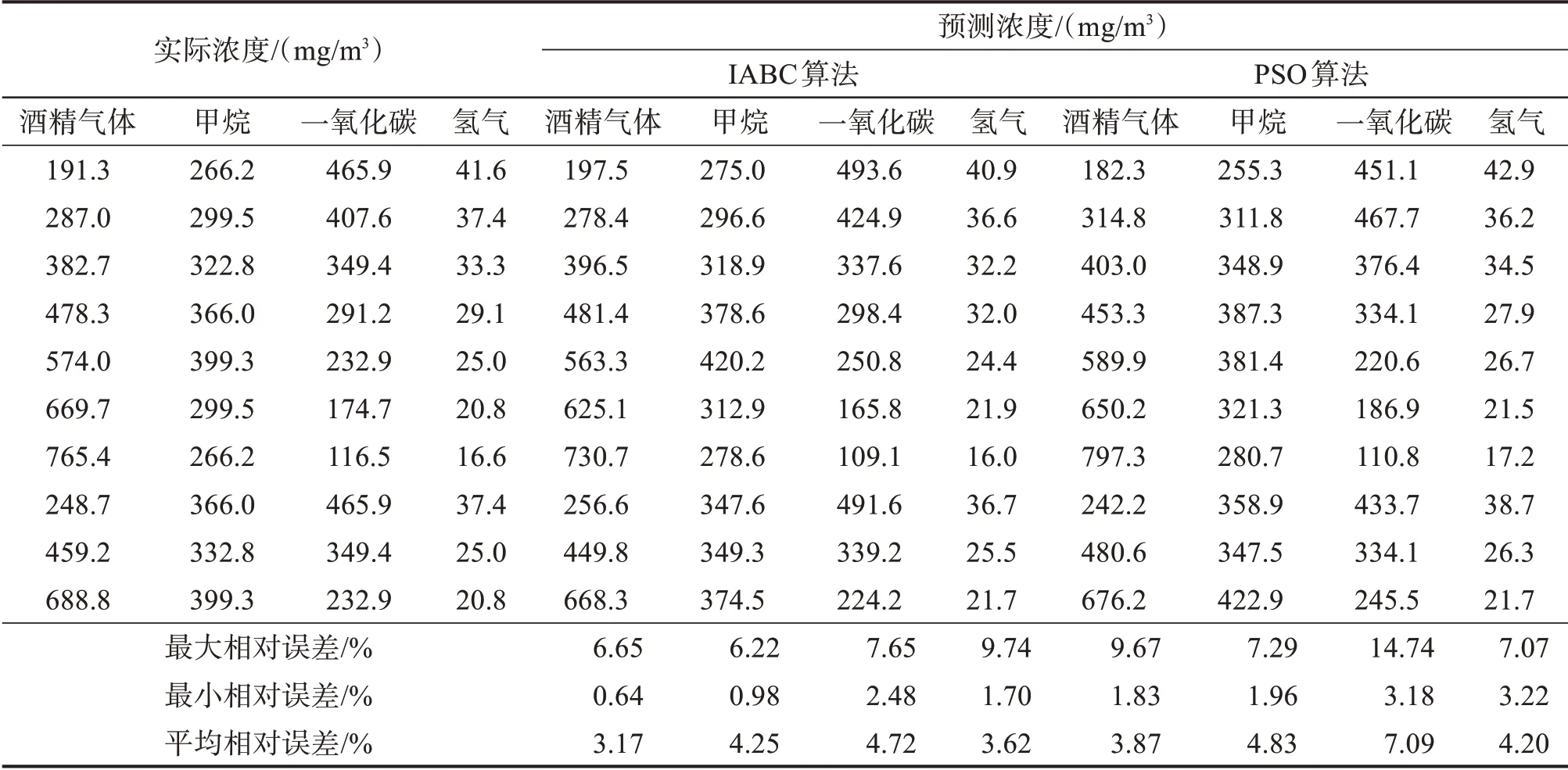
表5 基于IABC-LSSVM和PSO-LSSVM的混合气体各组分浓度测试结果Table 5 Test results of concentration of each component of mixture gas based on IABC-LSSVM and PSO-LSSVM

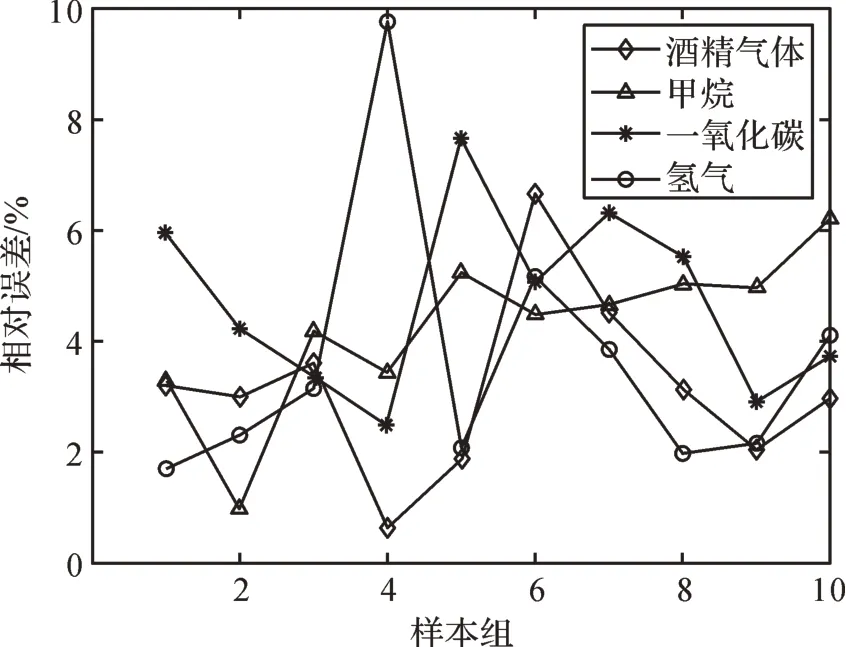
图8 基于IABC-LSSVM 的混合气体各组分浓度预测的相对误差Fig. 8 Relative error of concentration prediction of each component of mixture gas based on IABC-LSSVM

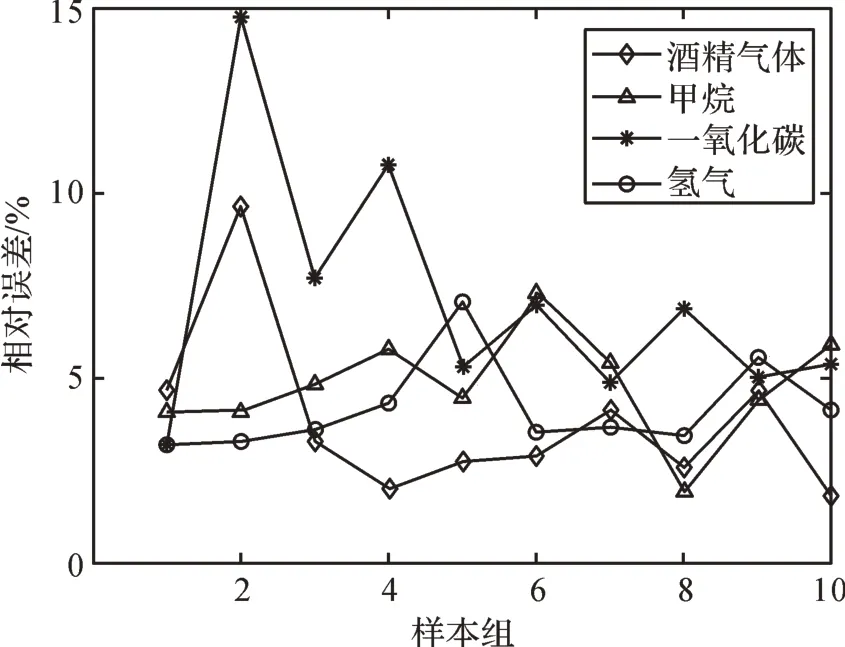
图9 基于PSO-LSSVM 的混合气体各组分浓度预测的相对误差Fig. 9 Relative error of concentration prediction of each component of mixture gas based on PSO-LSSVM

通过表5、图8、图9可以看出，基于IABC算法和PSO算法所建立的定量分析模型对混合气体各组分浓度的预测误差水平是不同的。采用IABC 算法优化LSSVM 后对各组分气体浓度预测的平均相对误差分别为3.17%（酒精气体）、4.25%（甲烷）、4.72%（一氧化碳）、3.62%（氢气），低于PSO 算法优化LSSVM后预测的平均相对误差（3.87%（酒精气体）、4.83%（甲烷）、7.09%（一氧化碳）、4.20%（氢气））。结果表明IABC算法优化的LSSVM在交叉敏感状态下对混合气体各组分浓度的预测精度要优于PSO算法优化的LSSVM，且IABC 算法比PSO 算法具有更强的鲁棒性。

4 结 论

本文提出了一种利用IABC 优化LSSVM 的方法，并将它应用于交叉敏感状态下混合气体的定量分析。通过在标准ABC算法中引入自适应递减因子，并结合轮盘赌和反向轮盘赌选择机制来改进待工蜂跟随概率公式，提高了算法的收敛精度。利用IABC算法优化LSSVM的参数，并使用优化后的参数重建定量分析模型，以提高对混合气体各组分浓度的测量精度。

通过5 个常用的基准测试函数对IABC 算法和PSO算法进行测试后表明，IABC算法具有更高的收敛精度。混合气体定量分析实验表明，采用IABC算法对各组分气体定量分析模型进行优化，优化所用的总时间和各模型的均方误差均低于采用PSO 算法的；利用优化后的各组分气体定量分析模型对混合气体各组分浓度进行预测，IABC-LSSVM 对混合气体各组分浓度预测的平均相对误差也低于PSO-LSS-VM。因此，在交叉敏感状态下，利用IABC算法优化LSSVM 的方法可有效提高混合气体各组分浓度的测量精度。