基于GA-NLP的剪刀式折叠桥梁展桥机构多目标优化设计
张 帅,韩 军,涂群章,杨小强,杨 旋
(1. 陆军工程大学野战工程学院,江苏南京210007;2. 陆军工程大学训练基地,江苏徐州221004;
3. 陆军研究院第5研究所,江苏无锡214035)
传统的军用剪刀式桥梁展桥机构主要通过驱动链条或钢索进行桥节的展开与折叠,其缺点是可展机构在运输状态下伸出桥面,增大了桥梁占用空间,导致桥梁设备机动性能降低。而新型剪刀式桥梁采用的内置式展桥机构,无论在展开状态还是折叠状态下均位于桥节内部,具有结构简单、质量较轻等特点,其内置展桥油缸可同时承载压力和推力作用,而且该展桥机构能够实现相邻桥节接近180°的回转,满足展开与折叠要求。某型军用剪刀式折叠桥梁需要在敌火力打击环境条件下架设,运输时桥节折叠放置在运载车辆上,架设时通过展桥油缸驱动展桥机构进行桥节的展开[1],展桥机构作为架桥和撤收的驱动机构,需满足动作可靠、迅速的工作要求[2-3]。由于展桥机构置于桥节内部,动作空间有限,不合理的设计会导致桥节展开过程中出现展桥机构铰点和展桥油缸的受力过大,降低展桥机构的使用寿命,甚至出现机构干涉碰撞以及机构死点的情况。因此,对现有工程样机的展桥机构进行优化设计来提升其受力性能具有较大的工程意义。由于展桥机构的受力状态比较复杂,常规的设计软件一般无法满足该机构的优化设计要求,因此针对新型展桥机构,需要寻求一种更为合理和有效的优化方法。
针对展桥机构或可展结构的优化,曾繁琦等[4]利用虚拟样机技术建立了展桥机构的参数化模型,将展桥油缸受力最小作为优化目标,利用广义梯度递减法对4 个铰点位置的变量进行优化;Dai 等[5]针对一种剪刀铰式可展结构,以设计空间、运动学和动力学限制为约束条件,以质量最小为优化目标,采用序列二次规划算法进行了优化设计;Jalili,Kaveh等[6-8]针对不同的可展桁架,分别选取不同的优化策略进行了桁架结构优化;Salar等[9]采用遗传算法对一种剪刀式可展机构进行了优化;胡均平等[10]基于粒子群优化算法对螺旋钻机变幅机构铰点位置进行了优化。
某型剪刀式折叠桥梁工程样机在实测过程中出现了展桥油缸间断溢油现象,通过对其展桥机构进行运动学和静力学分析发现:展桥机构各个铰点受力峰值差异较大;展桥油缸的拉力峰值大于其闭锁力,这与实测过程中展桥油缸出现间歇溢油的现象吻合;展桥油缸的推力峰值与拉力峰值的比值为0.67,与其理论比值1.2相差较大,说明展桥油缸受力分配不合理。为解决这些问题,需对展桥机构进行优化设计,优化时应满足:展桥机构展开过程中,各个机构之间及展桥机构与桥节之间不会发生干涉碰撞;展桥机构避免通过死点位置;液压油缸的伸长比例满足设计要求;边桥节与支腿之间的夹角在合理取值范围内。以展桥机构关键铰点和展桥油缸的受力最小为优化目标,采用遗传算法和非线性规划混合算法对展桥机构进行多目标优化设计。
1 展桥机构运动学与静力学数学模型
1.1 剪刀式折叠桥梁展开方案
某型剪刀式折叠桥梁由3个桥节组成,分别为2个岸桥节和1 个中桥节,桥节之间采用铰接方式连接。运输时3个桥节折叠放置在运载车辆上,以减小占用空间,方便运输。架设时,通过桥节之间的展桥机构进行展开。为方便表述,记与舌形臂油缸连接的岸桥节为第1桥节,中桥节为第2桥节,另一侧岸桥节为第3桥节。
剪刀式折叠桥梁展开方案如图1所示,折叠桥梁的架设步骤如下:第1步,当运载车辆到达架设位置后,通过翻转架油缸(图1中未画出)将水平放置的折叠桥推至竖直状态,如图1(a)所示。第2步,舌形臂油缸推动折叠桥,使它与竖直方向的角度为θ1,如图1(b)所示。第3步,第1桥节与第2桥节之间的展桥油缸动作,推动第1桥节与第2桥节展开,如图1(c)所示。第4步,第2桥节与第3桥节之间的展桥油缸动作,第2 桥节与第3 桥节展开,如图1(d)所示。第5步,舌形臂油缸动作,使桥梁放下直至到达工作位置。
鉴于第1 桥节与第2 桥节之间的展桥机构和与第2桥节与第3桥节之间的展桥机构完全相同,对称设置在第2桥节的两侧,第1桥节与第2桥节之间的展桥机构在架桥过程中承受2个桥节的重量,而第2桥节与第3桥节之间的展桥机构仅承受1个桥节的重量,因此本文仅对受力情况较恶劣的第1桥节与第2桥节之间的展桥机构进行优化分析。
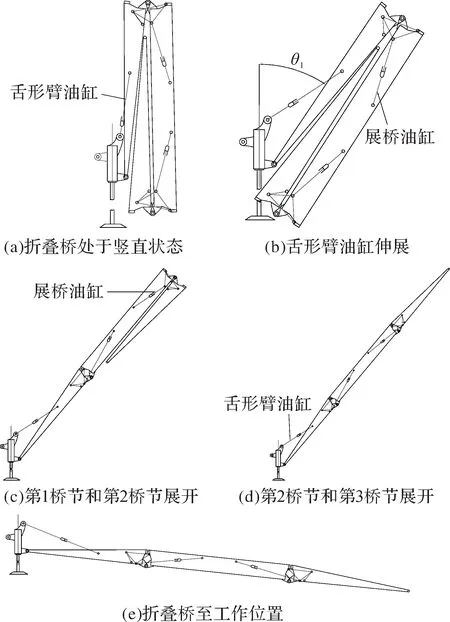
图1 剪刀式折叠桥梁展开方案Fig. 1 Scissor folding bridge unfolding scheme
1.2 展桥机构运动学模型
图2为新型剪刀式折叠桥梁展桥机构简图,其中A、B、C、D、E、F分别表示支腿与舌形臂油缸、舌形臂油缸与第1桥节、第1桥节与连杆、第2桥节与展桥油缸、连杆与展桥架、展桥油缸与展桥架的铰接位置;G1、G2分别表示第1桥节、第2桥节的重心位置。
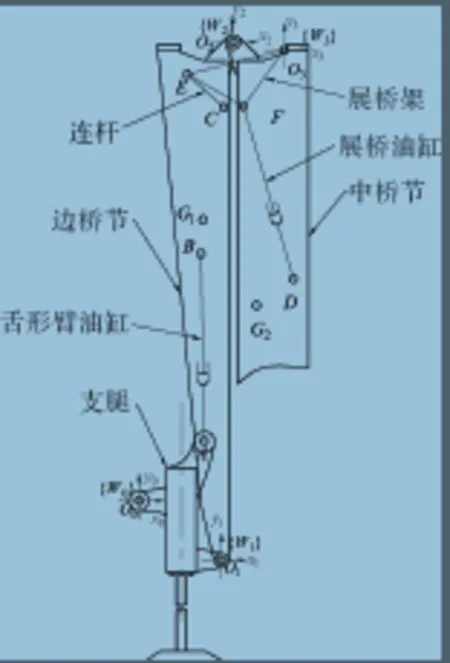
图2 剪刀式折叠桥梁展桥机构简图Fig. 2 Diagram of scissor folding bridge deployable mechanism
舌形臂油缸控制第1桥节的展开和折叠,展桥油缸控制第1桥节、第2桥节的展开和折叠。为了简化模型,将第2桥节和第3桥节作为整体,统称为第2桥节,其质量为第2桥节和第3桥节质量之和。
为了便于分析展桥机构的展开过程,假定展桥过程中支腿不动,以车辆与支腿的铰接点O0为坐标原点,建立基坐标系{W0} ;以支腿与第1 桥节的铰接点O1为坐标原点,建立坐标系{W1} ;以第1桥节与第2桥节的铰接点O2为坐标原点,建立坐标系;以第2 桥节与展桥架的铰接点O3为坐标原点,建立坐标系。设θ1为坐标系{W1} 相对于坐标系的旋转角度,θ2为坐标系相对于坐标系的旋转角度,θ3为坐标系相对于坐标系的旋转角度[11-12]。
利用Denavit-Hartenberg 法,建立剪刀式折叠桥梁展桥机构各坐标系间的转换矩阵[13],为:
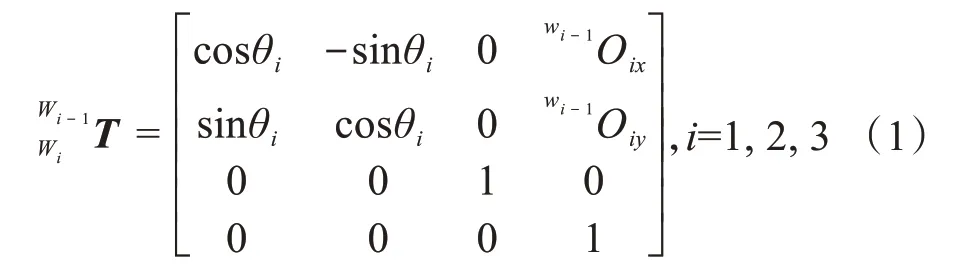
式中:WWii-1T为坐标系相对坐标系的转换矩阵;wi-1Oix、wi-1Oiy分别为铰点Oi在坐标系中的横坐标和纵坐标。
铰点C、O2在坐标系{W1} 下的坐标向量为W1C、W1O2;铰点D、O3、G2在坐标系{W2} 下的坐标向量为W2D、W2O3、W2G2;铰点E、F 在坐标系{W3} 下的坐标向量为W3E、W3F,则铰点C、O2、D、O3、G2、E、F在基坐标系{W0}下的坐标向量分别为:
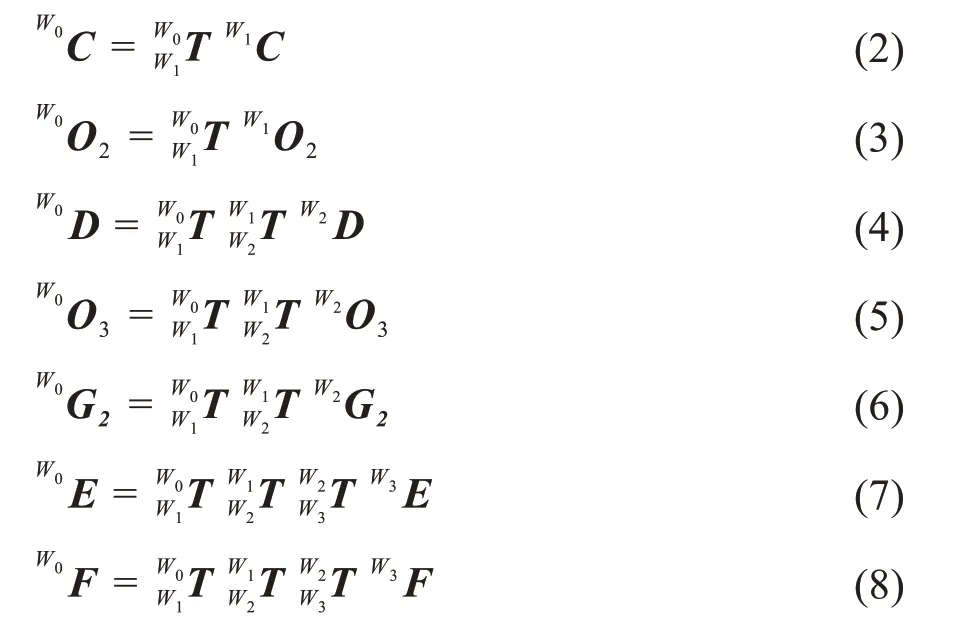
1.3 展桥机构静力学模型
以展桥机构和第2桥节为研究对象进行受力分析。如图3 所示,以铰点O2为坐标原点建立直角坐标系,x轴方向为水平向右,y轴方向为竖直向上,其中:m1、m2、m3分别表示展桥架、展桥油缸和第2桥节的质量;γ为连杆与竖直方向所成夹角;FCE为连杆受到的作用力,方向沿CE方向,FO2x、FO2y分别为铰点O2处受力沿水平方向和竖直方向的分力。
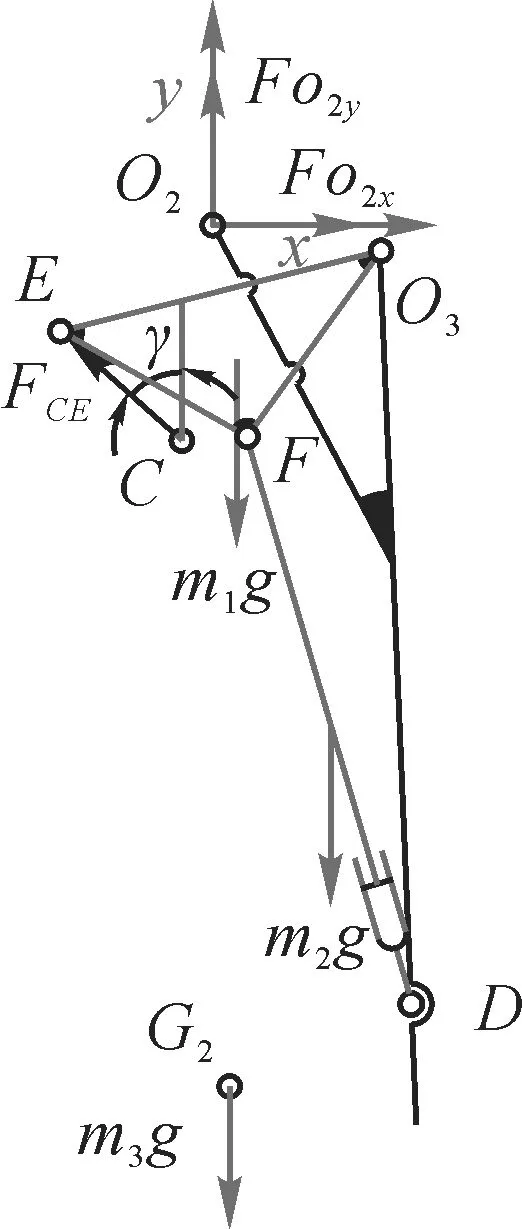
图3 展桥机构和第2桥节受力分析Fig. 3 Force analysis of deployable mechanism and the second bridge unit
由水平方向受力平衡得:
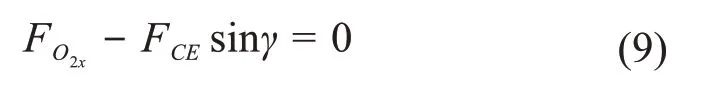
由竖直方向受力平衡得:
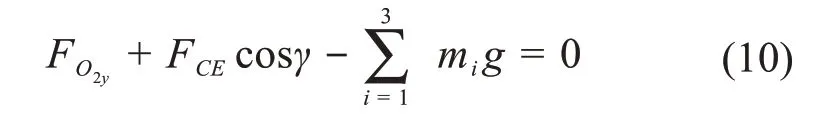
由铰点O2处转矩平衡∑MO2= 0得:
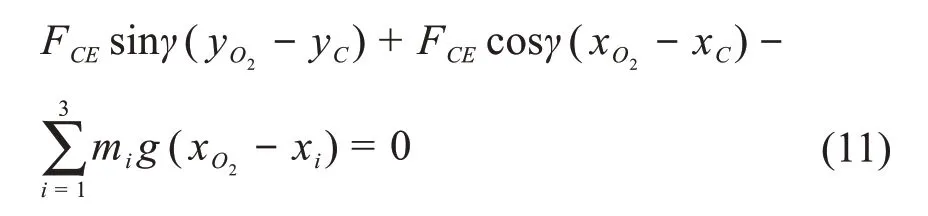
式中:x1、x2、x3分别为展桥架、展桥油缸、第2桥节质心位置的横坐标;xO2、xC分别为铰点O2、C的横坐标;yO2、yC分别表示铰点O2、C的纵坐标。
铰点O2所受的力为:
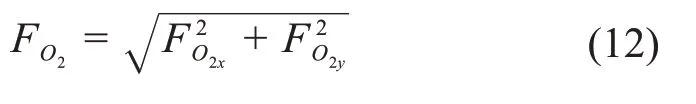
联立式(9)至式(12),可得FCE、FO2的值。
以展桥机构为研究对象进行受力分析。如图4所示,以铰点O3为坐标原点建立坐标系,x轴方向为水平向右,y 轴方向为竖直向上,其中:FDF为展桥油缸所受的力,受推力时为正,受拉力时为负;FO3x、FO3y分别为铰点O3所受力沿水平方向和竖直方向的分力;φ为展桥油缸与竖直方向所成夹角。
由水平方向受力平衡得:
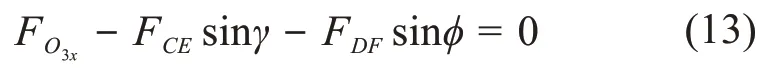
由竖直方向受力平衡得:
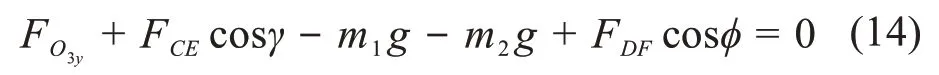
由O3铰点处转矩平衡得:
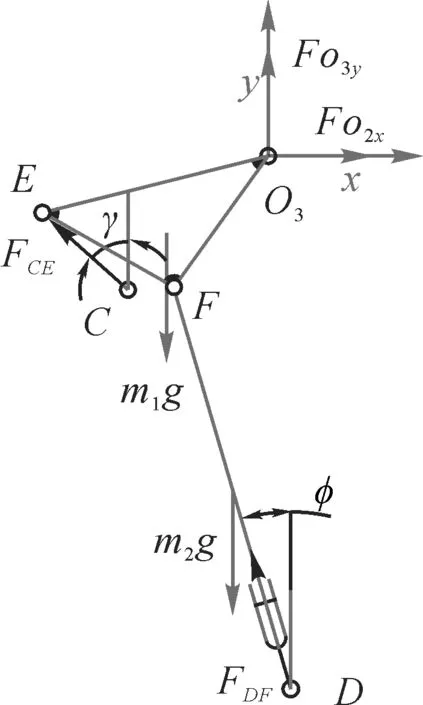
图4 展桥机构受力分析Fig. 4 Force analysis of deployable mechanism
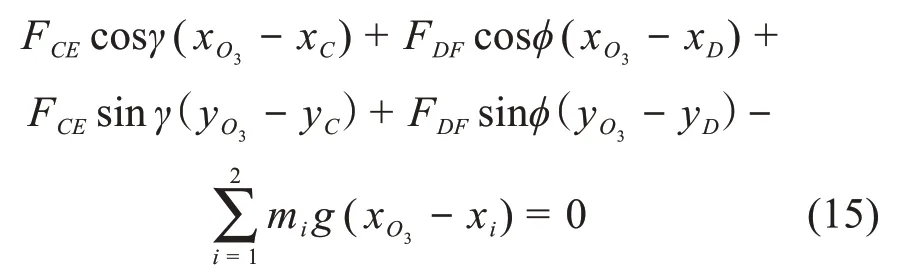
式中:xO3、xD分别为铰点O3、D 的横坐标;yO3、yD分别为铰点O3、D的纵坐标;
铰点O3所受的力为:
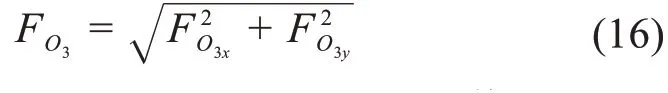
联立式(13)至式(16),可得FDF、FO3的值。
2 展桥机构多目标优化分析模型建立
2.1 设计变量
在架桥过程中,展桥机构受到大变载荷的作用,连杆、展桥架和展桥油缸的尺寸以及安装位置对展桥机构受力影响较大。取初始状态下展桥机构关键铰点C、D、E、F的坐标位置作为优化设计变量。
此外,θ1值不同时展桥机构的受力也不同,因此,在优化展桥机构参数的同时,需寻求θ1的最优值。故对于展桥机构,待优化的设计变量为:
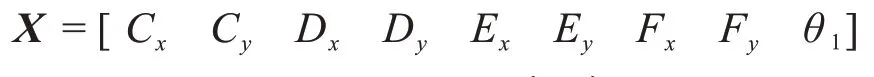
式中:Cx、Cy为铰点C在坐标系{ }W1下的坐标;Dx、Dy为铰点D在坐标系{ }W2下的坐标;Ex、Ey,Fx、Fy分别为铰点E、F在坐标系{W3}下的坐标。
2.2 约束条件
在设计展桥机构时,需要避免架桥过程中机构与桥节之间发生干涉碰撞,同时满足加工安装的工艺要求,因此需要将各个铰点的位置限定在一定范围内。根据工程经验,θ1的取值范围为-30°~-50°:当θ1取值过小时,展开后桥在竖直方向暴露面积过大,桥身重心偏高,同时易受风载影响,导致架桥过程不稳定;当θ1取值过大时,桥身重心偏低,桥节的展开空间受限,不利于桥节的快速展开。因此设定各个设计变量的线性约束如下,其中各点坐标值的单位为m,θ1的单位为(°)。

在设计展桥机构时,还应避免在架桥过程中出动作现力臂过小的情况,否则会导致展桥机构因受力过大而损坏,无法完成架桥动作。如图5所示,在桥梁展开过程中,当连杆与O2C共线时,连杆CE的受力对O2点的驱动力臂为0 m,这时无法对铰点O2产生有效力矩,不能使第2桥节绕铰点O2转动,连杆受力无限增大,此时为展桥机构的死点位置。尽管不会发生机构干涉,但无法完成目标动作。因此在展桥过程中必须避免这一情况出现,故设定架桥过程中需满足5°≤∠ECO2( X )≤175°。
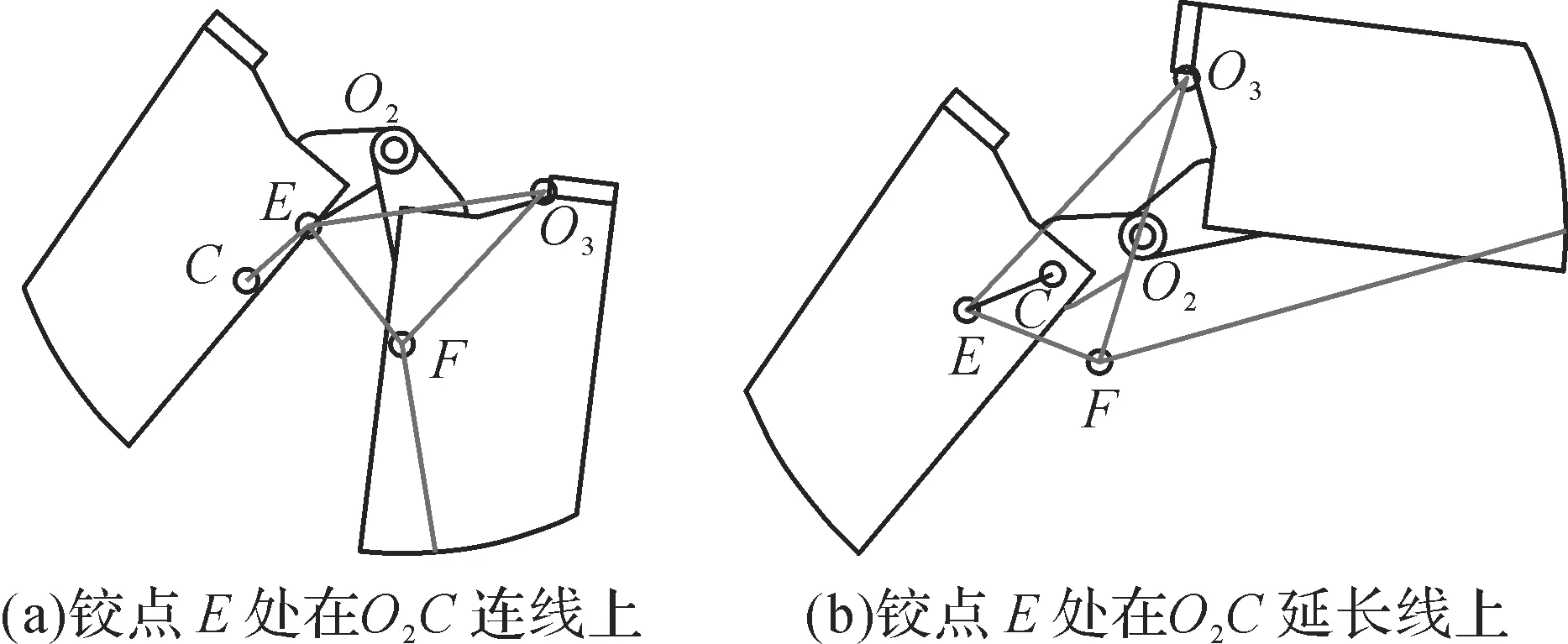
图5 展桥机构死点位置分析Fig. 5 Analysis of dead point for deployable mechanism
当θ2为174.3°和0°时,铰点D与铰点F之间的距离分别对应展桥油缸的最大伸展长度lDFmax(X)和最小长度lDF0( X ),应满足液压油缸设计的极限比例要求,即:
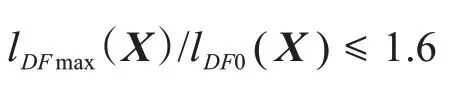
2.3 目标函数
展桥机构优化设计的目的是尽可能降低展桥机构各个对受力敏感位置处的受力峰值,优化展桥机构整体受力状况。展桥机构中对受力敏感的位置包括:铰点C、E、O2、O3、D、F,连杆以及展桥油缸。
由于展桥油缸所受的力与铰点D、F所受的力近似相等,但展桥油缸的极限受力更小,对受力也更加敏感,在展桥油缸和铰点D、F中,选择对展桥油缸的受力峰值进行优化。由于连杆CE 所受的力与铰点C、E所受的力近似相等,但连杆对受力更敏感,因此对连杆的受力峰值进行优化。综上,确定4个优化目标,分别为展桥油缸、连杆、铰点O2、铰点O3在架桥过程中的受力峰值。
对于典型的多目标优化问题,通常采用多目标加权法进行处理[14]。但是,由于各个优化目标的极限载荷不同,在加权处理前需对优化目标进行正规化处理[15]。展桥油缸小腔所能承载的最大拉力和大腔所能承载的最大推力是有区别的,对展桥油缸的拉力和推力分别作正规化处理:
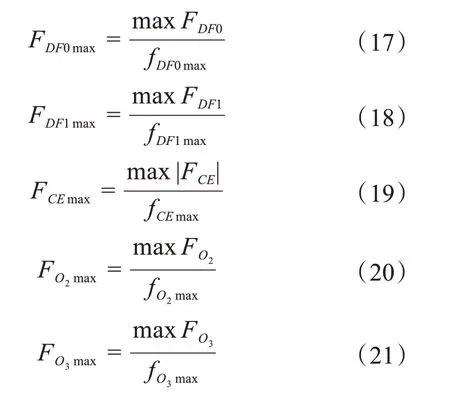
式中:fDF0max为展桥油缸承受推力的最大极限载荷;fDF1max为展桥油缸承受拉力的最大极限载荷;fCEmax为连杆的最大许用力;fO2max、fO3max分别为铰接处的最大极限载荷。
由此可得展桥机构的优化目标函数为:
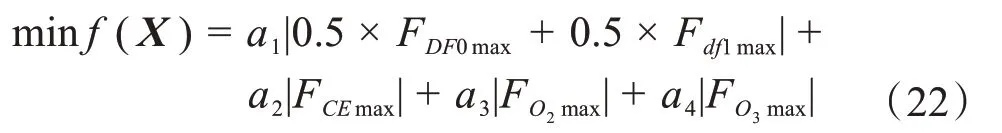
式中:a1、a2、a3、a4分别为展桥油缸、连杆、铰点O2、铰点O3处受力的权重系数,其值可根据实际经验选取,只需使权重系数满足关系:a1+ a2+ a3+ a4= 1。结合各个铰点和展桥油缸的受力敏感和优先程度,本文选取a1= 0.5,a2= 0.2,a3= 0.15,a4= 0.15。
综上所述,展桥机构的优化模型为:
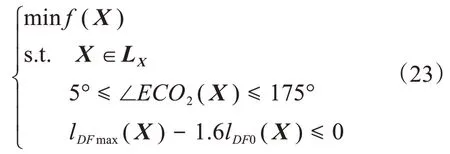
3 展桥机构多目标优化分析模型求解
3.1 优化算法
在多目标优化问题求解中,遗传算法全局搜索能力较强,但局部搜索能力不足;非线性规划具有较强的局部搜索能力,但易陷于局部解,发生早熟现象。通过结合2种算法的优点,首先利用遗传算法进行全局寻优,然后采用非线性规划进行局部寻优,则可以较高的搜索效率取得全局最优解[16-18]。
设定遗传算法种群规模为20,交叉概率为0.6,变异概率为0. 1,最大进化代数为60 代。如图6 所示,在优化设计变量的取值范围内随机产生种群,根据目标函数,得到不同的个体适应度,按照遗传算法进化法则依次进行选择、交叉、变异以产生新的个体。遗传算法每进行10次迭代,对所有种群进行一次非线性规划寻优,以加快算法的寻优速度。当达到最大迭代次数时,退出循环,输出最优解。

图6 基于遗传算法和非线性规划的优化流程Fig. 6 Optimization flow based on genetic algorithm and nonlinear programming
3.2 优化结果
基于遗传算法和非线性规划对展桥机构的参数进行优化,每代目标函数最小值和平均值如图7 所示。由图可以看出针对展桥机构的多目标优化模型,该混合算法具有较快的全局搜索能力。优化前后展桥机构设计变量如表1所示。
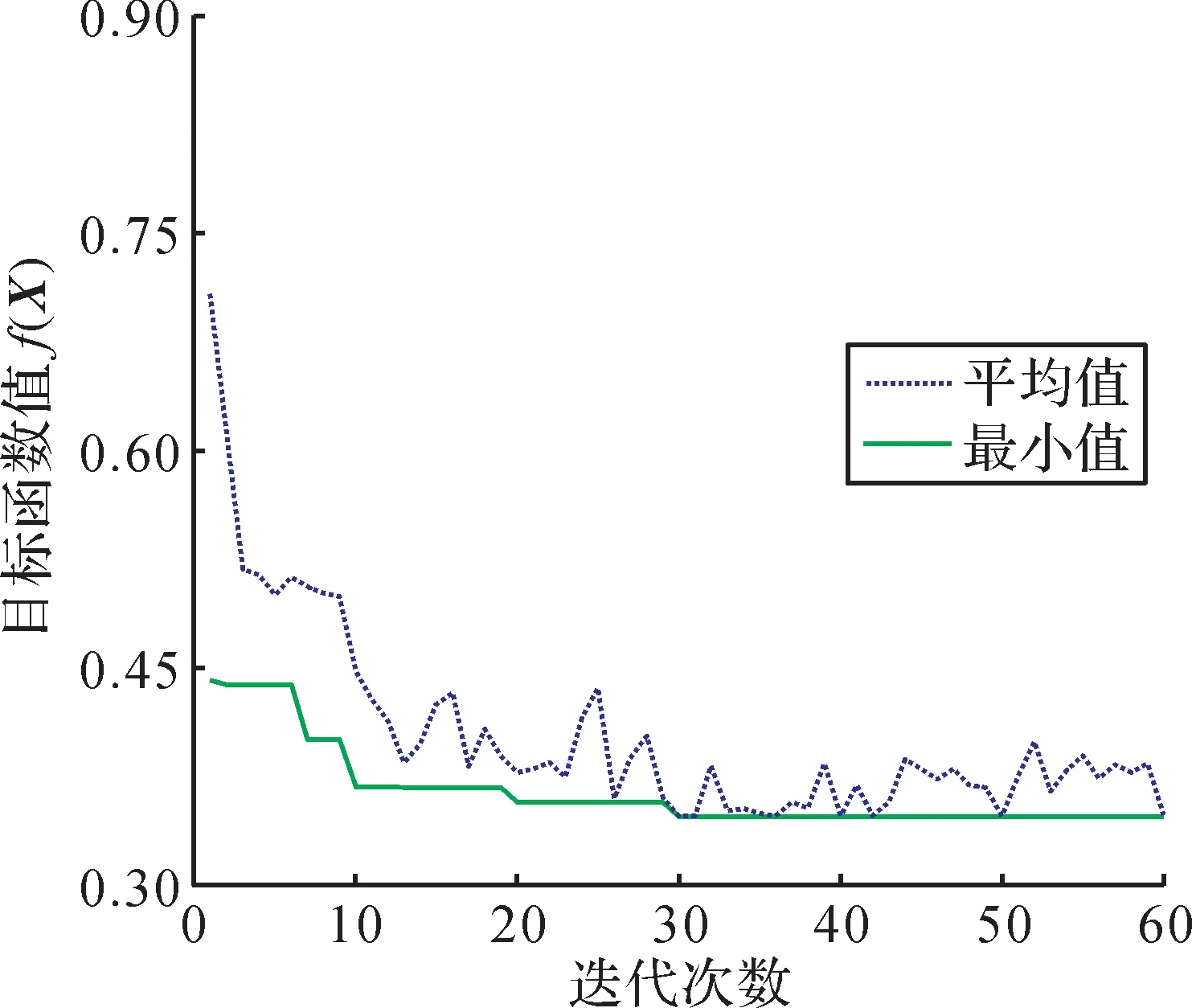
图7 展桥机构优化分析模型每代目标函数的最小值和平均值Fig. 7 The minimum and average values of the objective function of each generation for optimization analysis model of deployable mechanism

表1 优化前后展桥机构设计变量Table 1 Design variables of deployable mechanism before and after optimization
图8所示为优化前后展桥油缸的受力比较。由图可知,在初始参数下:当θ2=0°时,展桥油缸受到的最大拉力为-2.680×105N;当θ2=26.30° 时,展桥油缸受到的作用力为0 N;当θ2=174.30°时,展桥油缸受到的最大推力为1.775×105N。参数优化后:当θ2=0°时,展桥油缸受到的最大拉力为-1.129×105N;当θ2=28.08°时,展桥油缸受到的作用力为0 N;当θ2=96.48°时,展桥油缸受到的最大推力为1.326×105N。由此可知:通过优化,展桥油缸在架桥过程中承载的拉力峰值减小了57.9%,推力峰值减小了25.3%,展桥油缸所受推力峰值与拉力峰值的比值为1.17,更加合理;优化后展桥油缸受力方向改变时,其受力变化曲线的斜率明显更小,说明优化后展桥油缸由于受力方向的改变对液压系统造成的液压冲击也会减小。
图9所示为优化前后连杆的受力比较。由图可知,在初始参数下:当θ2=0°时,连杆受到的最大压力为1.034×105N;当θ2=36.72°时,连杆受到的作用力为0 N;当θ2=91.44°时,连杆受到的最大拉力为-1.520×105N。参数优化后:当θ2=0° 时,连杆受到的最大压力为0.4634×105N;当θ2=28.44° 时,连杆受到的作用力为0 N;当θ2=93.24° 时,连杆受到的最大拉力为-1.124×105N。比较优化前后连杆的受力可知:最大压力减小了55.2%,最大拉力减小了26.1%。
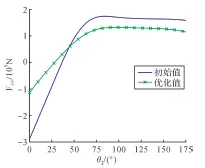
图8 优化前后展桥油缸的受力比较Fig. 8 Comparison of the force of deployable mechanism cylinder before and after optimization
图10 所示为优化前后铰点O2的受力比较。由图可知:优化前,当θ2=93.24°时,铰点O2在架桥过程中的受力峰值为1.664×105N;优化后,当θ2=100.80°时,其受力峰值为1.273×105N。优化后铰点O2的受力峰值相较于优化前减小了23.5%。
图11 所示为优化前后铰点O3的受力比较。由图可知:优化前,当θ2=92.16°时,铰点O3在架桥过程的受力峰值为2.208×105N;优化后,当θ2=124.56°时,其受力峰值为1.617×105N。优化后铰点O3的受力峰值相较于优化前减小了26.8%。
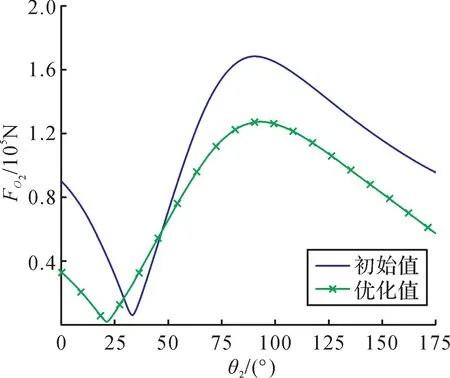
图10 优化前后铰点O2的受力比较Fig. 10 Comparison of the force of hinge point O2 before and after optimization
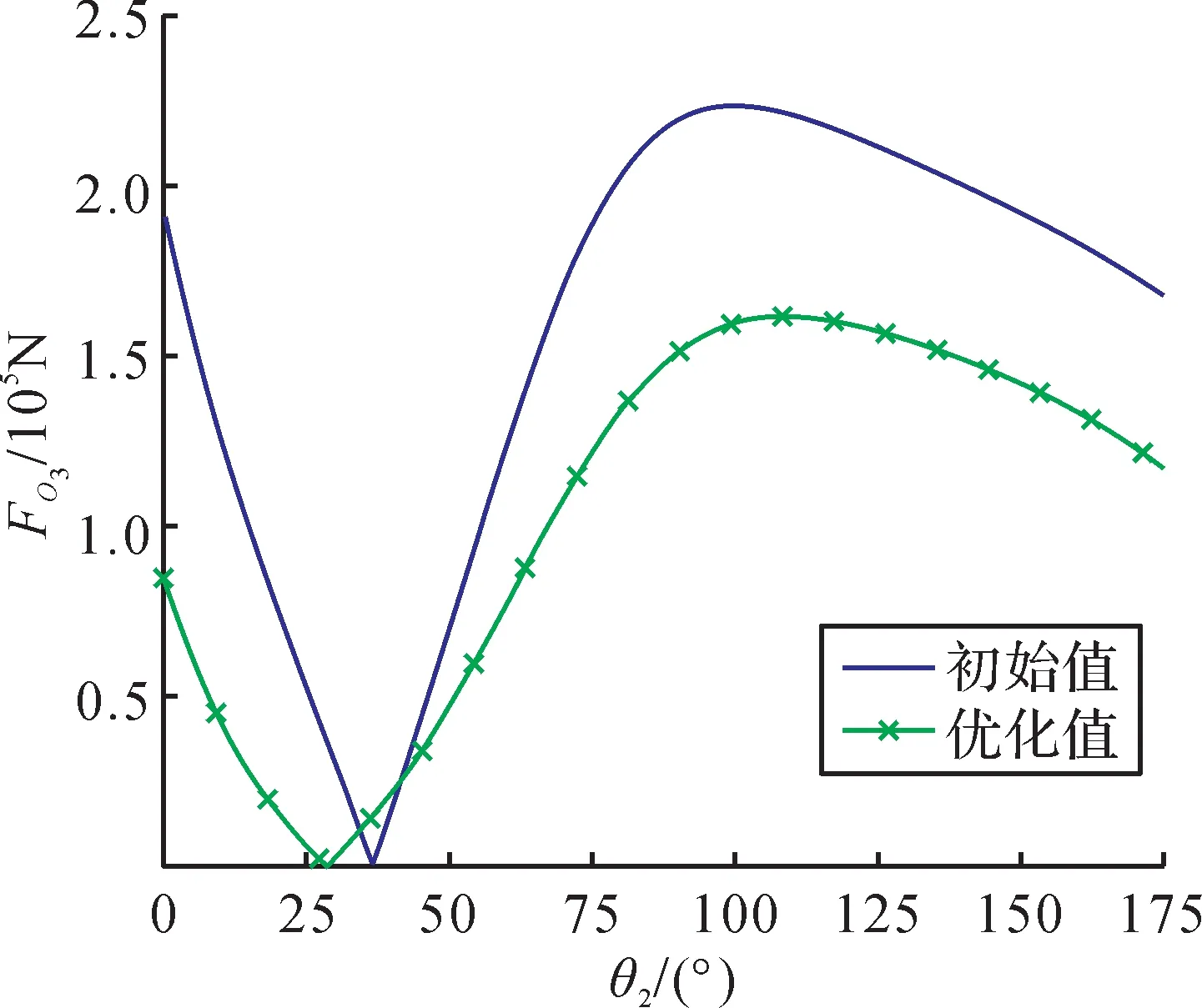
图11 优化前后铰点O3的受力比较Fig. 11 Comparison of the force of hinge point O3 before and after optimization
综上所述,优化后展桥油缸、连杆、铰点O2、铰点O3在架桥过程中所承载的最大力都有所减小。同时随着第1桥节、第2桥节的展开,其受力变化曲线更加平缓,有利于减小大变载对展桥机构铰点处轴承以及展桥油缸液压系统的冲击。
4 剪刀式折叠桥梁虚拟样机模型验证
根据剪刀式折叠桥梁样机的实际几何参数、物理特性及约束条件,基于ADAMS建立剪刀式折叠桥梁虚拟样机模型,如图12所示。根据所建立的虚拟样机模型对展桥机构进行展开过程的动力学仿真验证[19]。
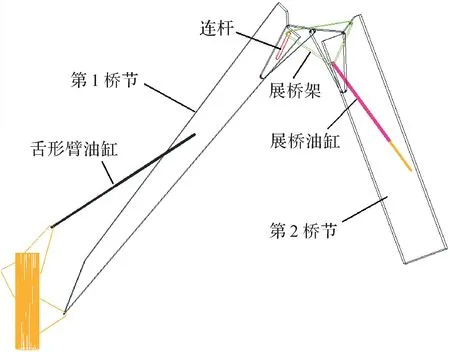
图12 剪刀式折叠桥梁虚拟样机模型Fig. 12 Virtual prototype model of scissor folding bridge
建立剪刀式折叠桥梁虚拟样机模型后,分别输入展桥机构优化前后的参数进行仿真,并对比展桥机构受力的仿真结果与数学模型计算结果,结果表明动力学模型与数学模型求解出的展桥油缸、连杆和铰点的受力值近似相等,验证了数学模型的正确性。为免赘述,仅以展桥油缸为例予以说明。图13为基于虚拟样机技术的展桥油缸受力分析结果。
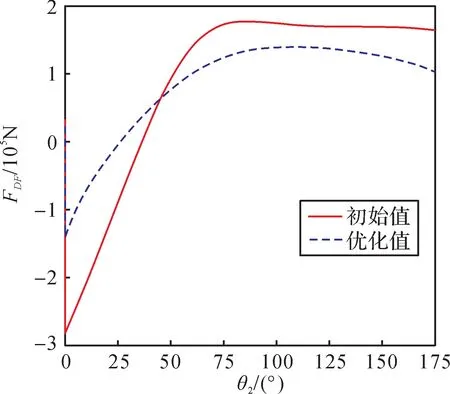
图13 基于虚拟样机技术的展桥油缸受力分析结果Fig. 13 The force analysis results of deployable mechanism cylinder based on virtual prototype technology
由图13可得:优化前展桥油缸受到的最大拉力为-2.780×105N,最大推力为1.778×105N;优化后,展桥油缸受到的最大拉力为-1.162×105N,最大推力为1.367×105N。仿真结果与数学模型计算结果有一定的偏差,经计算,偏差最大的为优化后展桥油缸受到的最大拉力,其偏差为3.7%。考虑到ADAMS 是基于动力学进行建模,仿真过程中会存在动载荷的作用,而数学模型为静力学模型,理论上存在偏差。经计算展桥油缸、连杆、铰点O2、铰点O3在架桥过程中受力峰值偏差都在5%以内,这说明基于数学模型的优化可很好地改善架桥过程中展桥机构的受力。
5 结 论
为改善剪刀式折叠桥梁展桥机构的受力,采用多目标优化的方法对展桥机构进行了优化设计,得出以下结论:
1)对4 个铰点的位置参数和1 个转角参数进行优化,使得展桥机构在架桥过程中的受力得到有效减小。优化后,展桥油缸承载的最大拉力和推力、连杆承载的最大拉力与压力、铰点O2和铰点O3的受力峰值相较于优化前分别减小了57.87%和25.3%、26.1%和55.2%、23.5% 和26.8%。结果表明优化后展桥机构受力得到明显改善。
2)基于遗传算法和非线性规划的混合算法具有不易早熟、收敛速度快的特点,可以有效解决新型剪刀式折叠桥梁展桥机构的优化设计问题。

