平均时距对良态风气候地区极值风速的影响研究
全 涌,肖钰川,顾 明
(同济大学土木工程防灾国家重点实验室,上海 200092)
在风气候观测数据格式方面,不同的国家存在很多的差异,其中在风速时距的选取上尤为突出。这是由于时距的选取不仅与各国的气候条件有关,还与历史规范的继承与延续有关。历史上,各国的规范中时距有1 min、2 min、10 min、1 h等。例如:设在关岛的JTWC (联合台风预警中心)对最大风速的测量采用1min平均时距[1],而RSMC (日本气象厅的区域气象中心)采用世界组织所规定的 10 min平均时距[2]。而中国气象局编制的《地面气象观测规范》等规范[3—4]对最大风速的测量以前使用的是2 min的平均时距,近年则使用10 min的平均时距。而对于在同一种风环境下预测不同重现期的风速极值,不同的观测时距必然会产生不同预测结果。这种差异同样存在于结构风荷载设计参考风速的选取中,一般情况下,若时距越长,所得到的平均风速样本就越小,最终得到的极值风速预测值也越小。Durst[5]基于短期风速观测结果,给出了1 s~10000 s的时距转换系数,但由于样本少,对长时距观测风速并不准确;林雯等[1]给出了特定台风条件下特定地区 1 min ~10 min时距与平均风速的衰减函数,并研究了不同时距对台风强度计算值的影响,但其时距选取的范围仍旧偏小;陈雯超等[2]给出了台风条件下不同时距风速系数的转换公式,但其结果均是依据某次特定台风得到,结论需要更多的个例进行验证;黄鹏等[6]给出了特定台风条件华东地区不同时距下湍流度、阵风因子、峰值因子及湍流积分尺度等风特性参数的变化规律,但未涉及时距对极值风速预测的影响。Mike Gibbons等[7]研究了充分数据与不充分数据下极值分布以及母体分布的区别,提出对于风速的母体分布,二者相对较符合;对于风速的极值分布,二者差异随重现期不同而不同,但未考虑风速观测时距的影响。Harper等[8]在若干台风实测数据的基础上给出了针对海上、陆地、离岸和离海几种不同下垫面的不同时距台风风速的转换系数,但其研究仍局限于台风,且其转换系数仅是对采样样本的修正,不能对年极值风速预测值等进行修正。
本文基于互联网上获得的美国良态风气候地区11个气象站的风速、风向长期连续观测数据[9—10],结合改进的独立风暴法和极值I型概率分布,得到时距跨度从1 min~60 min的不同重现期极值风速转换比例,以解决良态风气候地区风速观测时距不统一的问题。
1 风速样本的选取与预处理
美国国家海洋和大气管理局(ASOS, NOAA)近期公布了一个相对新的数据集,提供了从2000 年~2016年这16年间处于良态风气候地区的美国11座城市每分钟平均风速数据,城市所在位置如图1所示。此数据的测量是在当地空旷平坦地面上10m高处观测得到,数据样本量充足,完整性高。本文经过对这些数据的处理,分别得到了每1 min、2 min、3 min、…、60 min平均值样本,并对这些数据进行了分析,如图 2所示(以美国中部城市托皮卡市(Topeka,简称 TOP)为例)。
图1 11座城市所在位置Fig.1 Location of 11 cities

图2 TOP市1 h内不同时距风速处理结果示意Fig.2 Wind speed of TOP city at different average time intervals in one hour
从图2可以看出,即使对于在同一种风环境下预测不同重现期的风速极值,不同的观测格式必然会产生不同预测结果。极值风速的平均时距较小,所得的极值风速就较大。
2 不同采样时距对应的极值拟合与预测
本文初步采用独立风暴法进行计算。关于如何识别独立风暴,对于适当的非连续风速时程和连续风速时程,Cook[11]已经阐述了相应做法。
Harris[12—15]给出了一套相对完整的极值理论。与过去的所有极值分析方法相比,这套理论更加着眼于极值的特性,并为其量身打造了相应的拟合方法,尽可能地削减了极值分析过程中可能造成的误差。基于此,本文采用了改进后的独立风暴法:考虑左截断,并对简化变量的计算方法进行改进[16],同时采用加权最小二乘拟合极值Ⅰ型分布,以使得独立风暴法得到的拟合结果更符合实际。拟合效果和长周期重现期预测如图3、图4所示。

图3 TOP市不同时距下极值风速概率分布Fig.3 Probability distribution of extreme wind speed at different average time intervals in TOP city
图3可以看出,改进后的独立风暴法能很好地对极值风速进行拟合及预测。同时,经过不同采样时距方式处理后风速的观测极值会有差异,即不同的采样时距必然导致不同的风速预测极值。图4是根据拟合结果计算的1 年~1000 年重现期的风速极值。
图4可以看出,随着重现期的加长,基于不同采样时距所求得各重现期的极值风速有明显差异。同时,对其他 11座城市研究的结果表明:不同采样时距所求得极值风速之间存在一个转换比例,以50年重现期为例,在1 min采样时距下的风速极值均为10 min时距的1.19倍左右。
3 采样时距的转换比例
图5展示了将经过前述计算得到的各重现期下不同采样时距的极值风速值的结果,折线为真实值连线。可见,随着采样时距的加长,极值风速值会逐渐降低,这与前文预测相符。
值得说明的是,由于本文采用的是更接近实际的滑动平均法(即采取每段时距的平均值,不重复使用数据),故会使极值风速值随采样时距的变化而波动,但该波动属于随机波动,可以通过取不同城市的平均值等方式加以消除。
上述分析基于以美国中部城市 TOP在不考虑风向情况下进行分析,该市的风气候类型为良态风,而具有良态风和台风混合气候类型其他城市在不同采样时距下所引起的差异可能会更大。因此,本文又对其他10个城市进行了分析。并以10 min时距下极值风速值为单位 1,得到了不同重现期各城市时距转换比例的综合图如图6所示,其中各细虚线分别代表美国各城市的时距转换比例,粗实线为上述城市的平均值;由于各城市的气候不同等原因,其各转换比例不完全相同,但整体趋势和变化范围类似。

图4 TOP市不同时距下各重现期极值风速预测Fig.4 Extreme wind speed for different return periods at different average time intervals in TOP city

图5 TOP市各重现期极值风速随采样时距变化趋势Fig.5 Variation trend of extreme wind speed with average time intervals for different return periods of TOP city

图6 11座城市各重现期不同采样时距转换比例图Fig.6 Conversion ratio of different average time intervals for 11 cities in different return periods
将10年、50年、100年重现期下各城市转换比例的均值进行分析,如图7所示,同时,运用指数函数拟合上述值,得到了改进的独立风暴法下综合拟合曲线和相应的拟合公式,并与Durst[5]基于短期观测数据给出的转换系数进行对比。

图7 时距转换比例图Fig.7 Conversion ratio of different average time intervals
图7表明,11座城市极值风速对于时距的转换比例均值几乎不随重现期变化,且其随采样时距的改变符合指数函数关系。通过与Durst的结果对比可以看出:与Durst给出的转换系数在1 min~10 min时距段上基本吻合,而在10 min~60 min时距段上存在差异。这是由于Durst的结果是基于某个观测站点的短期观测数据得出,数据量过少,导致其在10 min~60 min时距上转换系数稳定在1附近,显然这并不合理,不具有广泛代表性。
而本文基于美国11个城市16年连续观测数据得到的结果能反应出这一时距段上转换系数的变化。为工程应用简便,将得到的转换系数拟合为指数曲线,并对系数进行灵敏度分析,结果如下:

式中:t为观测时距;R(t)为该时距下极值风速转换为10 min标准时距极值风速时的转换比例。由此得到不同平均时距的极值风速之间的转换关系:
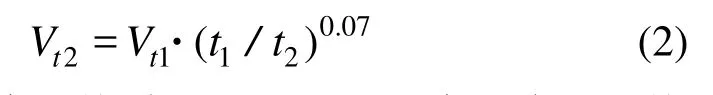
式中:t1和t2为平均时距;Vt1和Vt2为对应于平均时距t1和t2的极值风速。
图8给出了拟合值与真实计算值的结果比较。可见,无论在是长时距(10 min以上)还是在短时距(10 min以下)下,真实值和拟合值的残差率均在-2%~2%,通过进一步计算,该拟合函数相对于原始数据的和方差(SSE)为 0.005,均方根(RMSE)为0.0096,确定系数(R2)为0.978,这表明指数函数对不同时距间极值风速的转换比例具有很好的拟合效果。

图8 转换比例拟合效果分析图Fig.8 Analysis chart of conversion proportion fitting effect
4 结论
本文研究了良态风气候地区风气候观测时距差异对极值风速预测产生的影响。对美国处于良态风气候地区 11座城市气象站记录的每分钟连续观测数据进行分析计算,给出了平均时距为 1 min~60 min的不同重现期的极值风速,并得到良态风气候地区详细的不同时距下极值风速的转换比例,得到如下结论:
(1) 随着平均时距的增大,极值风速的预测值逐渐变小,近似呈指数律衰减;
(2) 运用 Harris改进的独立风暴法,不同城市之间由于气候等原因在时距转换比例的计算中存在5%~10%的差异;
(3) 平均时距对极值风速的影响规律基本不受极值风速重现期的影响;
(4) 从统计学角度分析,1 min平均极值风速与10 min平均极值风速大19%左右;
(5) 不同平均时距的极值风速可用式(1)和式(2)进行转换。

