木结构建筑群火灾蔓延危险建筑的识别及防火改造效果评价

张 健，宋志刚，李全旺，郝爱玲

(1. 昆明理工大学建筑工程学院，昆明 650500；2. 清华大学土木工程系，北京 100084；3. 应急管理部天津消防研究所，天津 300381)

中国现存大量木结构建筑群，据不完全统计，中国 48个世界遗产名录中有 16个与传统木结构建筑群相关，而待保护的传统村落更是多达2500 个[1]。木结构建筑群的消防安全是一个突出的问题，以云南省为例，2006年-2016年，大理古城、丽江古城和独克宗古镇三个著名古城先后发生火灾 34起[2]，其中丽江大研古城 3·11火灾(2013年)、香格里拉独克宗古镇1·11火灾(2014年)、丽江束河古镇4·06火灾(2014年)均导致了建筑群的火灾蔓延，在国内外引起了广泛关注。类似的火灾蔓延问题，在近几年的贵州、广西苗寨、侗寨等木结构杆栏式建筑群大火中，也时有发生。目前，虽然意识到火灾在木结构建筑群中蔓延的风险，但是由于文物或传统风貌保护的限制，火灾防控工作不允许对建筑群进行大规模改造，因此识别出对建筑群火灾蔓延影响显著的单体建筑，并进行相应的防火改造，对古城镇、古村落的保护具有重要意义。

火灾在建筑间蔓延是连片木结构建筑群火灾面临的普遍问题，国内外相关研究多集中在地震后次生火灾领域，比较常见的火灾蔓延模型有Hamada[3]提出的经验模型，黄维章等[4]、Nishino等[5]提出的概率模型，Ohgai等[6]、杨立中等[7]、柳春光等[8]提出的元胞自动机模型，Himoto和Takara[9]提出的物理模型，赵思健等[10]结合Himoto模型提出的简化物理模型等。在随后的研究中，Ren和Xie[11]将蔓延模拟技术和GIS平台结合，开发了地震后火灾仿真系统，曾翔等[12]对贵州苗寨及独克宗古城进行火灾蔓延分析，并基于OSG图形引擎开发了可视化平台。上述工作对建筑群火灾蔓延的研究具有重要的参考价值，但限于研究对象和考虑问题的出发点不同，大部分研究主要侧重于火灾在建筑群中蔓延过程、蔓延规模的描述与模拟及火灾蔓延发展过程的仿真再现，对火灾防控问题的研究相对较少。针对上述问题，本文以场-网数值模拟为基础建立了考虑多火灾场景的危险建筑的识别方法。该方法首先结合有向图模型建立蔓延矩阵和邻接矩阵；在此基础上提出节点危险度指标，并结合节点连通度得到节点重要度指标作为危险建筑的判定依据；随后给出了面向不同数量的防火改造建筑的确定方法以及防火改造效果的评价方法；最后对云南某典型木结构民居建筑群进行了模拟分析，验证该方法的有效性，并对改造效果进行了评价。

1 分析过程和方法

1.1 火灾蔓延模拟方法

场-网数值模型、Himoto模型[9]和简化物理模型[10]在模拟建筑群火灾蔓延时都采用了类似“网”的思想(Net work Model)，即将单体建筑模型化为节点，每个节点的温度、热释放速率等物理量采用一组均匀参数表示[13]，在此基础上，分析不同节点之间的引燃过程，从而确定连接节点的弧。场-网数值模拟涉及的基本概念和方法表述如下。

1.1.1 节点

将建筑群中每个单体建筑均看作一个节点，t时刻任意节点i的状态Si可用四个参数确定：

式中：t0i为节点被点燃时间，对于初始起火节点，t0i= 0，当节点未被引燃时，t0i可取一大值；Qi和Ti分别为节点 i的火灾热释放速率(HRR)和平均温度，均为 t和t0i的函数，当 t ＜ t0i时，表示节点i未被引燃，二者皆为0，当t≥t0i时，节点i处于燃烧状态，二者皆为燃烧时间 Δti(Δti=t- t0i)的函数。Himoto模型、简化物理模型和场-网数值模型的最大差别在于确定单体建筑 Qi和 Ti的方法。简化物理模型直接通过已有的经验确定单体建筑的 Qi和Ti，Himoto模型则是先将单体建筑划分为由若干房间组成的区域，结合区域模型(Zone Model)[9]求解区域的控制方程确定 Qi和 Ti，而场-网数值模拟在确定单体建筑 Qi、Ti时则使用了场模型(Field Model)[13—14]，即直接将整个单体建筑划分为若干微元体，运用计算流体动力学(CFD)的方法在分析域内求解质量、动量和能量等基本守恒方程，通过分析微元体构成的 N-S方程[15]模拟单体建筑物内气体的速度场、温度场和浓度场的空间分布及时间变化特性，从而确定不同燃烧时间下的Qi和Ti。

1.1.2 节点引燃状态的确定

热辐射、火羽流和飞火是建筑间火灾蔓延的主要途径。有关飞火的试验和计算理论还有待进一步完善，其分析结果尚存在一定的不确定性[16]，因此，已有文献主要研究热辐射和火羽流引起的火灾蔓延问题，相关研究已进行较多论述，这里仅进行简要归纳。t时刻，对于一个未起火节点j，当满足式(2)时，节点j被引燃：

式中：qcr为木材引燃的临界热通量，一般可取12.5 kW/m2；qjr(t)为节点 j的木质外墙或洞口接收到的热通量，可按如下公式计算[17]：

式中：ε为墙面发射率，可取 0.8；σ为 Stefan-Boltzman 常数，取 5.67×10-8W/(m2·K)；Ni为起火节点数量；iφ为第i个起火节点相对于节点j的木质外墙的辐射角系数； qi(t)为节点i的热辐射功率，借鉴NFPA92B的点火源的计算方法[18]，可近似按式(4)计算；hw为墙面对流换热系数，可由大空间自然对流换热实验关联式计算[14]，本文近似取7.6 W/(m2·K)，T0/K 为节点 j的墙面温度，TE为Ni个起火节点火羽流的等效叠加温度，按式(5)计算[17]。

式中：α为建筑外墙开洞率；χR为火灾热释放能量中以热辐射形式释放的比例，一般取1/3。

式中，ΔTi为起火节点i的火羽流引起的在节点j墙面处温度增量，ΔTi的计算方法详见文献[17]，这里不再赘述。火羽流在风作用下的偏转修正详见文献[9-10]，在分析计算时，可将未引燃建筑靠火羽流最近的表面按高度和宽度方向划分若干计算参考点，按式(3)计算各参考点的热通量，取其最大值确定建筑是否被引燃。

1.2 蔓延模拟的分析步骤

通过检查、更新t时刻各个节点的状态Si(t, t0i,Qi, Ti)实现建筑群火灾蔓延的模拟，模拟过程可按如下步骤进行。

1.2.1 单体建筑场模拟

本文使用美国国家技术标准与技术研究院(NIST)开发的火灾动力学模拟工具(FDS)进行单体建筑的场模拟，以确定单体建筑的 Qi(Δt)和 Ti(Δt)曲线(Δt=t - t0i)，并制成插值表供分析使用。值得注意的是：1) 由于模拟对象主要是木结构建筑，因此需要考虑木材的热解问题；2) 由于场模拟计算工作量很大，对所有建筑单体逐一模拟是难以实现的，考虑到我国古城镇建筑群往往是由几种建筑材料、尺寸、分隔方式、立面风格相近的基本建筑单元组合而成，因此，可仅对几种典型的建筑单元进行模拟，再推广至所有建筑中，从而大幅度减少模拟计算的工作量。

1.2.2 确定火灾蔓延模拟的初始条件

火灾蔓延模拟的初始条件包括：1) 环境风速、环境温度(T∞)等环境条件；2) 建筑群节点数量、模拟时间步长dt和模拟时间总步数 Nt等模拟条件；3) 节点初始条件，对于初始起火节点，其引燃时间t0i= 0，初始状态设置为Si= Si(0,0,0,T∞)，对于未起火节点，其引燃时间取一大值，计算时可取 t0i=(Nt+1)dt，其初始状态设置为Si= Si(0, (Nt+1)dt, 0,T∞)。

1.2.3 更新不同模拟时间tk= kdt，k=1,2,…, Nt时的节点状态

节点状态更新按如下方式进行：

1) 通过场模拟确定HRR和温度插值曲线，插值确定所有已起火节点(满足 t0i≤ tk)在 tk时刻的Qi和 Ti；

2) 按式(3)～式(5)计算所有起火节点对每一个未起火节点j (满足t0i=(Nt+1)dt)在tk时产生的总热通量qjr(tk);

3) 按式(2)判断未起火节点j是否被引燃，若节点j被引燃，则t0j= tk，节点j的状态被更新为Sj=Sj(0, tk, 0, T∞)。

为记录建筑火灾随时间蔓延的过程，可在上述模拟过程中设置一个1×M的行向量g作为模拟过程中的引燃时间向量，向量g的第i个元素记录节点i被引燃的时间。

1.3 火灾邻接矩阵和蔓延矩阵

在给定环境温度、风速等条件的情况下，设定一个或多个起火节点，按照上文所述方法均可确定一个引燃时间向量 g，该向量给出了每个节点被引燃的时间，从而确定出一个蔓延场景。针对不同的初始起火建筑，其位置、火灾热释放速率的不同会导致不同的蔓延结果，每一种蔓延结果均对应了一种蔓延损失场景。对于具有M个节点的建筑群，在考虑有m个初始起火节点的情况下，其蔓延场景数共个。

为说明问题，这里仅讨论一个初始起火点的情况，共计有M个蔓延场景，可确定出M个引燃时间向量gi，i =1,2,…, M。为反映出不同节点之间的直接引燃关系或者说网络中弧的连接状态，引入邻接矩阵 AM×M描述各蔓延场景中不同节点之间的直接引燃关系，若节点 i能直接引燃节点 j，则A(i, j) =1，否则A(i, j) = 0。考虑在密集建筑群中，不同单体建筑之间存在相互遮挡效应，在火灾蔓延途径以热辐射和火羽流为主的情况下，远一些的建筑会因遮挡效应而暂时得到保护，建筑起火后一般是先引燃其最邻近的建筑。因此，在获得第i个火灾蔓延场景向量gi以后，i场景的邻接矩阵A(i)可近似按如下步骤确定：

1) 按引燃时间由小到大的顺序对向量 gi对应的节点编号排序。排序越靠前的节点，起火时间越早，对于排序位置为j的节点，假设其节点编号为k，那么引燃节点k的节点，存在于排序位置为前j -1个的节点中；

2) 取前j -1个节点中距离k最近的节点，若其节点标号为m，则可确定编号为m的节点直接引燃了编号为k的节点，此时A(i)(m, k)=1；

3) 按排序结果，逐次执行第2步骤，最终确定第i个火灾蔓延场景所对应的邻接矩阵A(i)。

考虑所有火灾场景后，建筑群火灾蔓延的邻接矩阵AT可通过如下的布尔运算得到：

式中，矩阵的并，表示对矩阵中对应位置的元素进行并集运算。AT矩阵的第i行中取值为1的元素的列，表示节点i起火时，能够直接引燃的节点编号；AT矩阵的第j列中取值为1的元素的行，表示能够直接引燃节点i的节点的编号。由于风向的影响和建筑规模的差异性，节点i能直接引燃节点j，但节点j并不一定能直接引燃节点i，即建筑群存在由节点i向节点j单向火灾蔓延的情况，在存在单向蔓延时，AT为非对称矩阵。

由M个引燃时间向量g，可获得一个M×M的引燃时间矩阵G，矩阵元素Gij给出了第i个节点为初始起火节点时，第j个节点被引燃的时间，依据式(7)可进一步确定火灾蔓延矩阵 SM×M，当然，火灾蔓延矩阵也可由矩阵 AT结合有向图模型的遍历算法建立[19]。

矩阵S的第i行中值为1的列表示当第i个节点为初始起火点时，在模拟时间内被直接或间接引燃的节点，第j列反映第j个节点在不同火灾场景中被引燃的情况。

1.4 建筑危险度、重要度和损失期望

1.4.1 节点危险度Ri

对矩阵S的第i行求和：

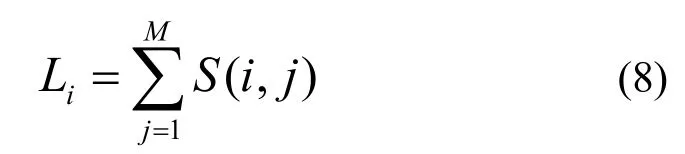
式中，Li表示当节点i作为初始起火节点时，最终被直接或间接引燃的节点数量。对矩阵S的第i列求和：

式中，Pi表示会引燃节点i的场景数量。显然，如果建筑群中某一节点的 Li越大，说明该节点起火时，能够直接或间接引燃的建筑数量越多，蔓延损失越大；在假定每个起火场景出现概率相同(均为1/M)的情况下，若该节点的Pi越大，说明该节点被引燃的概率也越大。因此，可以用指标Ri判断节点i在建筑群中的危险度，Ri越大，节点的危险度越高，Ri按式(10)计算：

1.4.2 节点重要度 Ii

在获得AT矩阵以后，可以计算任意节点i的连通度Ci：

式(11)中右侧第一项为节点 i能够直接引燃的节点数，第二项为能够直接引燃节点i的节点数，显然，Ci越大，节点i在整个网络中的“枢纽地位”越高，则节点i对局部或整体网络的影响力也越大。

节点危险度 Ri及节点连通度 Ci是评价网络中节点重要性的主要指标，在存在双向蔓延的情况下，在网络中会出现多个危险度相同的节点，但事实上，这些节点在网络中的连通度并不一样，或者说，其重要性是存在差异的，为此，引入重要度指标 Ii，Ii按式(12)计算：

以图1为例，该蔓延图示中各参数及相应的Ri、Ci计算结果如表1所示。结合表1的计算结果不难看出，尽管1号~5号节点具有相同的危险度Ri=3.43，但通过 Ii的计算，可以将危险度高、连通度大的3号节点找出来，对其进行拆除或采用自动灭火系统等防火改造措施，让其成为不蔓延建筑，使其断开与周围节点的联系，如图2所示。由图2可看出，对3号节点进行改造具有最好的改造效果，建筑群火灾蔓延的风险得到了有效的控制。

图1 节点危险度、连通度Fig.1 Node risk and connectivity

表1 火灾蔓延模型各参数指标Table 1 Parameters of fire spread model

图2 改造后节点危险度、连通度Fig.2 Node risk and connectivity after fire protection

对一个建筑群而言，可以通过逐次搜索重要度最大的节点，确定防火改造的建筑，具体步骤如下：

1) 设定起火点，得到不同火灾场景下的引燃时间向量gi，i =1,2,…, M；

2) 由引燃时间向量g确定i火灾场景的邻接矩阵A(i)；

3) 由邻接矩阵A(i)通过布尔运算得到整个建筑群火灾蔓延的邻接矩阵AT；

4) 由矩阵AT结合有向图模型的遍历算法建立火灾蔓延矩阵S；

5) 根据式(8)~式(12)确定 Li、Pi、Ri、Ci、Ii值；

6) 选取Ii值最大的节点作为防火改造建筑k，将AT中的k行k列置为0，更新AT矩阵；

7) 重复步骤4)~6)；

8) 给出需要防火改造建筑的先后顺序。

1.4.3 损失期望E(L)

显然，对于一个具有M个单体建筑的建筑群，按照上文提到的搜索办法，可以得到这M个建筑进行防火改造的优先级，并通过损失期望值[20]来评价改造效果。对各个场景下的Li值进行频数统计，可得到引燃节点数量L的累计概率密度曲线，如图3所示，对该曲线按式(13)进行积分，得到不同起火场景引燃建筑数量的期望值E(L)：

在考虑恢复重建时，也可以将E(L)视为片区发生火灾后，需要恢复重建的建筑数量期望值，E(L)越小说明区域抵御火灾蔓延的能力越强，可恢复性越好。

图3 引燃节点数量L的概率分布曲线Fig.3 Cumulative probability distribution of L

2 翁丁村火灾蔓延分析

2.1 翁丁村的建筑特点

翁丁村位于云南省沧源县，是我国典型的杆栏式古建筑群，除粮仓外，共有建筑105栋。现场测绘得到各单体建筑位置及编号如图4所示。典型单体为底部架空的双层结构，如图5所示，由于连片建设，存在火灾蔓延风险[21]。村内单体建筑均为全木结构、草屋顶，采用2 cm木板作为隔墙，建筑面积不大，依据其建筑面积，可划分为 6类，如表2所示。

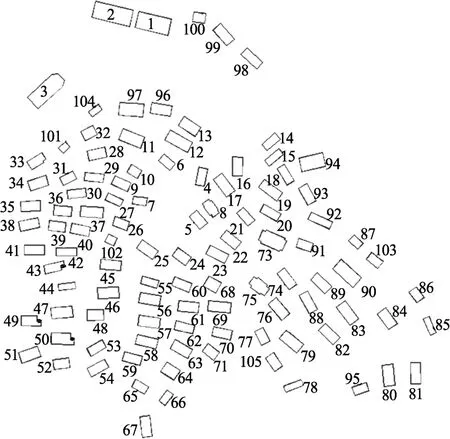
图4 建筑布局及编号Fig.4 Building layout and numbering

图5 典型杆栏式民居建筑图Fig.5 Typical railing style of ancient residential building

表2 建筑面积分类Table 2 Building area classification

2.2 单体建筑场模拟

本研究采用 FDS模拟各类单体建筑的 Q(t)、T(t)。FDS建立的典型单体建筑的几何模型如图 6所示，该建筑长 10.5 m，宽 5.2 m，建筑面积109.5 m2。通风开口为：1.5 m×0.7 m的门洞两个，墙体与屋盖之间的0.3 m×5.35 m通风口一个，墙体上设0.5 m×0.5 m的窗洞两个，屋顶两侧各设一底边长 2.5 m，高 1 m的三角形洞口。根据相关文献[21-22]，木材设定热解温度范围220 ℃~380 ℃，热解吸热5×103kJ/kg，燃烧放热1.8×104kJ/kg，茅草(屋顶)设定热解温度范围220 ℃~380 ℃，热解吸热1.7×103kJ/kg，燃烧放热 1.8×104kJ/kg。经计算得出单体建筑的Q(t)、T(t)，如图7、图8所示。

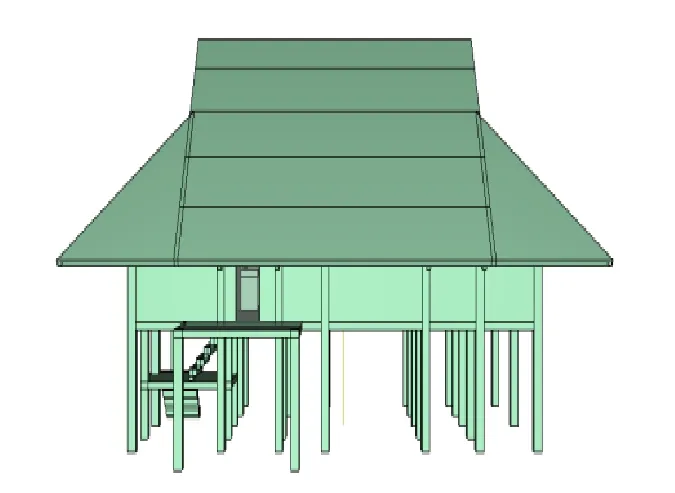
图6 FDS建模效果图Fig.6 FDS model of typical building

图7 典型建筑热释放速率曲线Fig.7 The heat release rate curves of typical building

图8 典型建筑温度曲线Fig.8 The temperature curves of typical building

2.3 建筑群火灾蔓延模拟

对应翁丁村105栋单体建筑，逐次设定起火点，每一起火点对应一种蔓延场景，共有105种火灾蔓延场景。建立每一场景的引燃时间向量 gi，i =1,2, …, 105，可在图上描绘出相应的火灾蔓延状态及蔓延路径。以 30号节点起火场景为例，该场景下火灾蔓延状态及蔓延路径如图9所示。各火灾场景蔓延途径的叠加可构建建筑群火灾蔓途径网络模型，如图10所示。

图9 第30号火灾场景蔓延情况Fig.9 No. 30 scenarios of fire spreading

图10 所有火灾场景蔓延情况Fig.10 All scenarios of fire spread

考虑所有火灾场景，通过式(6)、式(7)建立火灾蔓延的邻接矩阵AT及蔓延矩阵S，根据式(8)～式(12)分别求得各不同火灾场景下的节点连通度 Li、Pi、Ri、Ci及Ii如图11、图12所示。

根据上述确定建筑群改造节点的搜索算法，计算各火灾场景的重要度指标Ii，选取Iimax的节点作为改造节点 k，重新计算并确定新的改造节点，给出不同改造节点数量的Ii值曲线，如图13所示(限于篇幅，本文仅讨论前 9个优先级节点的改造效果)。确定翁丁村木结构建筑群改造节点的优先级为40、30、20、61、35、43、57、27、17，其相应的节点位置分布如图14所示。

分别对优先级为前9的建筑进行改造，计算考虑所有火灾场景下的不同改造节点数量的 Limax、Pimax、Rimax、Cimax及 Iimax值，如图 15所示。由图15可以看出，随着改造建筑数量的增加，火灾蔓延的各参数指标均呈现不同程度的降低，前2栋建筑的改造效果较为显著，但当改造建筑的数量超过一定值后，各参数指标的下降不再明显。

图11 不同火灾场景的Li及Pi值Fig.11Li and Pi for different fire scenarios

图12 不同火灾场景的Ri、Ci及Ii值Fig.12 Ri, Ci and Ii for different fire scenarios

对各火灾场景的Li值进行频数统计，计算引燃建筑数量L的累计概率密度曲线，如图16所示。并根据式(13)给出相应的损失期望E(L)曲线如图17所示。

由图16、图17可以看出，随着改造建筑数量的增加，火灾蔓延的期望损失E(L)逐渐降低，当改造建筑的数量超过5个时， E(L)逐渐趋缓，改造效果不明显。

结合上述分析，可根据L的累计概率分布曲线给出翁丁村建筑群的节点改造方案。图 16表明，在 95%保证率的要求下，当建筑群容许的 Li≤10时，需要改造优先级最高的2栋建筑，当建筑群容许的Li≤5时，需要改造优先级最高的4栋建筑。参考图17，当改造数量为5栋以上时，改造效果不明显，加大投入带来的回报并不理想，因此，可考虑翁丁村改造的建筑数量为5栋，其对应的改造节点的优先级为 40、30、20、61、35，位置详见图14，此时对应的E(L)值为1.67。

图13 不同改造节点数量水平对应的火灾场景Ii值曲线Fig.13 The Ii curves of different scenarios with different number of fire protected nodes

将翁丁村需改造的 5栋建筑剔除(拆除或采用自动灭火系统改造成不蔓延建筑)后，对其重新进行模拟，并对模拟结果进行对比分析，相应的 Li及Pi曲线见图18。

图15 不同改造节点数量的火灾场景最大指标变化Fig.15 The maximum change in indices among all fire scenarios with different number of fire protected nodes

图14 改造建筑的优先级序列及相应的位置分布Fig.14 The priority and corresponding locations of fire protected buildings

图16 不同改造节点数量水平下L的概率分布曲线Fig.16 The cumulative probability distribution of L under different number of fire protected nodes

图17 不同改造节点数量的E(L)曲线Fig.17 E(L) curves for different numberof fire protected nodes

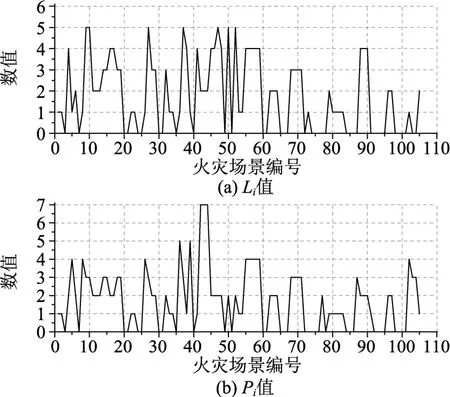
图18 改造后各火灾场景的Li及Pi曲线Fig.18 Li and Pi of different fire scenarios after fire protection

对比图11和图18可以看出，在仅改造5栋建筑的情况下，翁丁村建筑群 Limax=5，较未改造时(Limax=20)最大引燃建筑数量降低75%。由图17看出，改造5栋建筑后，火灾蔓延期望损失由5.39降到了1.66，降低69.2%。

3 结论

本文结合场-网数值模拟和有向图的基本原理，提出木结构建筑群火灾蔓延危险建筑的识别方法，并对危险建筑防火改造的效果进行了评价。结合云南翁丁村的火灾蔓延防火改造，研究表明：

(1) 该方法能够确定出建筑群中危险的单体建筑，结合搜索算法，可进一步确定建筑群中改造建筑的优先级，在此基础上，结合损失期望值，确定出容忍损失期望下的建筑改造数量。

(2) 算例分析表明，采用上述方法，通过对少数危险建筑的拆除或加强，可以大幅度降低火灾发后引燃建筑的数量。依据改造效果及损失期望给出的改造节点序列，在仅改造少量(105栋中的 5栋)建筑的情况下，能使改造后火灾蔓延期望损失降低69.2%，最大引燃建筑数量降低75%。

(3) 该方法只需对各火灾场景进行一次定量化的模拟，确定最危险建筑，删除改造建筑后可通过修正邻接矩阵的方式进行结果的预判，不需对各火灾场景进行重复模拟，减少大量的火灾蔓延模拟工作。