Riesz定理在证明测度收敛性质中的应用

孙秀花

（晋中学院数学学院，山西晋中030600）

依测度收敛是实变函数中一类重要的收敛，Riesz 定理给出了函数列依测度收敛的一个充要条件。测度收敛的性质基本都是用定义来证明的，利用该定理来证明测度收敛的性质有时会简单的多。主要通过例子来说明Riesz 定理在证明测度收敛性质中的应用，并且用该定理得出函数列测度收敛的一个充要条件。

1 预备知识

定义1设fn(x)是可测集E上的可测函数列，f(x)是E上的可测函数。如果对每个ε＞0，有

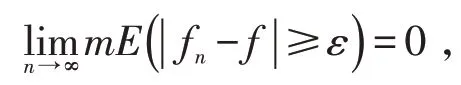
则称序列fn(x)依测度收敛于f(x)。记为

定理1（F.Riesz 定理）设mE＜∞，则可测函数列fn(x)在E上测度收敛于f(x)的充要条件是：对序列{fn(x)}的任何子列{fnk(x)}，都存在子列几乎处处收敛于f(x)。

定理2（关于可测集的性质）设在可测集E上，则

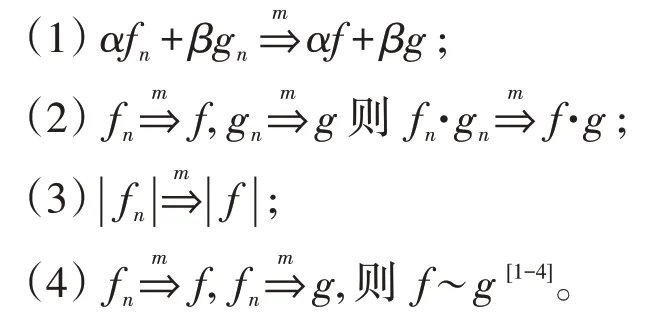
2 利用Riesz定理证明测度收敛的性质

下面给出定理2的证明。

例1设在可测集上，利用Riesz定理证明：

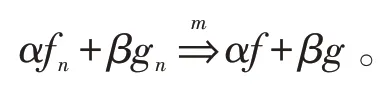
证明由定义易得设 {αfn,k+βgn,k} 是{αfn+βgn} 的任一子列，则{αfn,k} 是{αfn}的 子 列 ，根 据 定 理1 有{αfn,k} 的 子 列(i→ ∞ )。相应地，{βgn,k,i} 是{βgn} 的子列，根据定理1有{βgn,k,i} 的子列注意到{αfn,k,i,j} 是 {αfn,k,i} 的子列, 也有从而有{αfn,k+βgn,k} 的子列(j→∞ )。由于 {αfn,k+βgn,k} 是{αfn+βgn} 的任一子列，根据定理1得

例1 说明怎样用定理1 来证明测度收敛的性质，并不比用定义简单，下面再举一个例子，下面例2如果用定义来证明非常麻烦，好多实变函数书上用了很大篇幅来证明，这里用Riesz 定理给出证明。

例2设在可测集E(mE＜ +∞ )上证明

证明方法1，用定义证明[5]。

方法2，设{fn,k·gn,k} 是 {fn·gn} 的任一子列，则{fn,k} 是{fn} 的子列，因为由 Riesz 定理有{fn,k} 的子列相应地，{gn,k,i} 是{gn}的子列，根据Riesz 定理有{gn,k,i} 的子列(j→∞ )。注意到 {fn,k,i,j} 是{fn,k,i} 的子列，也有

类似地，关于测度收敛的其他几个性质都可以用该定理证明。

3 主要结果

下面给出测度收敛的一个充要条件

定理3在可测集上，f且

证明必要性显然。

充分性设{fnk}是{fn} 的任一子列，则{f2nk}是{f2n} 的子列，因为由定理1存在{f2nk}的子列相应地，的子列，因为由定理 1 存在的子列注意到的子列，也有从而有{fnk}的子列(j→ ∞) ,由定理1得

通过以上性质的证明和结论可以看出用Riesz定理来证明可测集的性质时，关键就是转化为几乎处处收敛的性质。因为几乎处处收敛与处处收敛只差一个零测度集，而处处收敛的性质已经比较成熟，所以推导起来比较简单。