基于模糊神经网络的人体摔倒特征参数算法研究

谭晓静

(闽南理工学院电子与电气工程学院，福建石狮362700)

我国随着老龄化趋势日趋明显，针对老年人的健康监护等相关问题越来越受到政府和组织机构的重视。研究发现，老年人在运行状态中有较高的致病率，伴随摔倒，使其具有很高的住院率和死亡率[1]。关于国内外学者关注对老年人监控设备开发，对摔倒检测及报警方面，做了很多研究[2-3]。在现有研究成果的基础上，提出基于模糊神经网络的人体摔倒检测方案，利用运动数据、脉搏信号和温度作为特征参量进行数据融合算法，通过网络模型进行实验验证。

1 检测控制系统硬件结构

人体温度传感器选用MAX30205MTA，工作电压 2.7 ～3.3V，测温范围 370C ～ 390C，测量精度0.10C；运动状态信号传感器选用GY-9250，内部低压差稳压，供电电源3 ～5V，内置AD转换器，16位数据输出；脉搏心率传感器选用MAX30102，主要用于智能监测设备用于心率和血氧监测，利用光反射（PPG）检测信号，LED峰值波长660 nm/880 nm，采用5V 独立电源，可实现电源始终维持供电状态。系统硬件设计结构如图1所示。

图1 系统结构框图

2 模糊神经网络

2.1 模糊神经网络模型

提出的模糊神经网络共6层，模糊神经网络结构如图2所示。

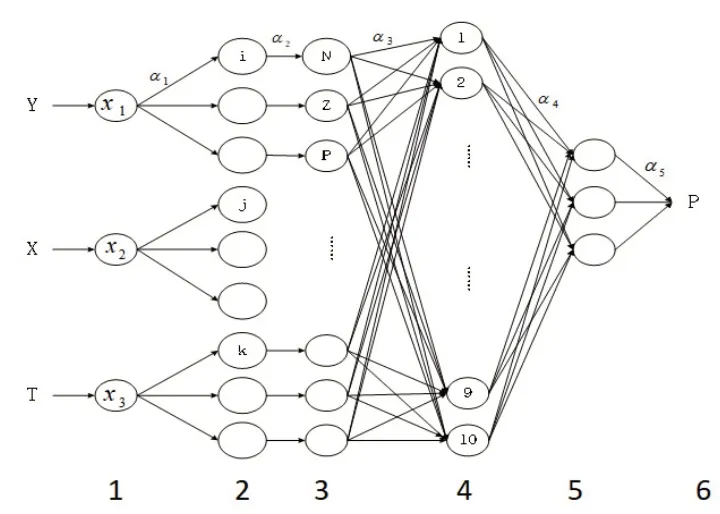
图2 模糊神经网络结构

其中，第1 层为输入层，用于输入人体的运动状态、脉搏、体温监测数据的信息，用Y，X，T表示，经线性化处理得到3 个输入参数，用x1,x2,x3表示；

第2层对线性变换层，对输入变量通过权值进行线性连接；

第3 层为模糊化层，主要对第1 层输出量进行模糊化处理。通过计算隶属函数，得到输入点对于语言变量值模糊集合有最大隶属度；通过模糊推理，用于实现模糊规则制定，测量模糊规则的适用度，选取符合实际判断意义的模糊规则，用N、Z、P 代表模糊推理规则中的“负”、“零”、“正”；

第4层为归一化层，用于实现对前层输出结果的归一化处理；

第5 层为去模糊化层，计算并输出“正常N”，“摔倒S”，“心率不齐导致摔倒L”[4-5]所发生的概率；

第6层为反模糊化层，将模糊输出量转换成事故判定结果。

算法设计流程如图3所示。

图3 算法设计流程图

2.2 模糊神经网络机构

在模糊化处理中，选取合适的隶属函数对计算网络的输出量有重要影响。根据模型建立的实际需求[6-7]，利用隶属度函数将输入量以“N(负)”、“Z(零)”、“P(正)”表示，“N(负)”和“P(正)”采用S型函数隶属表示，“Z(零)”采用高斯函数隶属表示。模糊神经网络的输入节点有3 个，第2 层选取3 个模糊分割数对第1 层输入量进行分割，节点数有9 个。推理模糊层每个参数有3种状态，即模糊股则应该有33条规则，结合实际情况，选取10条具有实际判断意义的模糊规则如下：

① if(Y is N)and(X is Z)and(T is N)then(结果为N)；

② if(Y is N)and(X is N)and(T is N)then(结果为N)；

③ if(Y is P)and(X is Z)and(T is N)then(结果为L)；

④ if(Y is Z)and(X is P)and(T is N)then(结果为L)；

⑤ if(Y is Z)and(X is Z)and(T is N)then(结果为L)；

⑥ if(Y is N)and(X is N)and(T is P)then(结果为S)；

⑦ if(Y is N)and(X is Z)and(T is P)then(结果为S)；

⑧ if(Y is P)and(X is Z)and(T is Z)then(结果为S)；

⑨ if(Y is P)and(X is P)and(T is P)then(结果为S)；

⑩ if(Y is P)and(X is P)and(T is Z)then(结果为S)。

2.3 神经网络各层单元计算

线性处理层：

其 中，A取Y,X,T，r取 值i,j,k，分别 取1,2,3。

模糊化层：

其中，A取（Y，X，T），i取（1,2,3），α1，α2为连接权值，选取任意值作为初始值，对其进行训练可使改变隶属函数参数发生改变。

模糊推理，输入变量(x1，x2，x3)的隶属度函数有3个，以y表示“N(负)”、“Z(零)”、“P(正)”3个状态。

l为第四层节点个数。

归一化层：

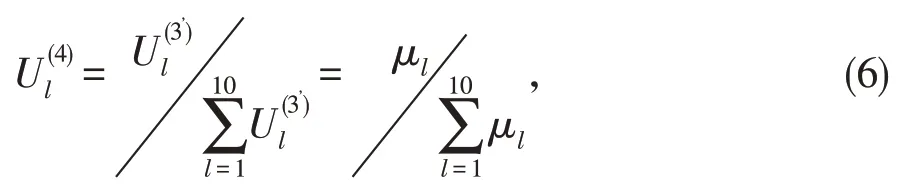
其中，l为去模糊化层的节点数，l取值(1,2,3，…，10)。

去模糊化层，该层主要根据“正常N”，“摔倒S”，“心率不齐导致摔倒L”所发生的概率。

利用加权平均法得到精确的输出结果。

最终确定模糊神经网络的拓扑结构为3-9-9-10-3-1。

2.4 改进BP神经网络权值修正

有效训练网络权值，可使神经网络实际输出与期望输出尽可能接近。网络设计中权值α1，α2，α4采用L-M算法，参数在训练时取最大值，当接近最佳值时，参数逐渐减小到零。开始学习时误差较大，L-M算法采用高斯牛顿法，当误差变小，使用梯度下降法[8-9]。

调整高斯牛顿方法的权重公式如下：

其中，H为损失函数在w(k)处的海塞阵列，∇E为损失函数E在w(k)处的导数阵列，DH是海塞阵列的对角排列阵列。μ的调整公式：

3 算法模拟仿真

实验测试人员为35～55岁的人群，采集50组样本数据，进行处理作为样本数据，选取其中30组训练神经网络模型，其过程在MATLAB 环境下进行仿真测试。在模糊神经网络中设置训练误差为1×10-5，最大训练次数为1000次，分析结果可以看出，经过大概26 次迭代计算后，训练误差为6.1709×10-6，满足训练要求。网络训练过程如图4所示。

图4 网络训练误差曲线图

4 结果分析

选取实验数据10 组作为测试样本，在预定模型进行50 次测试，实验数据测试结果用表1表示，实验证明设计的摔倒报警器能准确检测有无摔倒以及事故情况下出现摔倒的概率。

表1 实验数据测试结果

5 结语

以多数据融合为指导思想，研究利用多种信号综合进行摔倒的检测，由于老年人在摔倒时往往会出现短时间的脉搏突变，以及考虑到部分老人患心脑疾病，利用脉搏判断进一步辅助摔倒检测。根据人体运动状态将人体摔倒过程的3个不同的状态组成，正常行走状态，由于物理原因导致摔倒，心率不齐导致摔倒。在此基础上，提出了一种基于模糊控制的神经网络模型，通过相关的判断算法，辅助判断摔倒出现的概率，可大大提高摔倒检测的准确率，降低误报率。